கணிதம்

கி.மு 3வது நூற்றாண்டின் கிரேக்க கணிதவியலாளர் யூக்ளிடின் (கிடுக்கிமானியை வைத்திருப்பவர்), ஓவியம் - ராபியேல் சான்சியோவின் கற்பனையில், ஏதென்சு கல்விக்கூடத்திலிருந்து.

கணிதத்தில் பல்வகை நுட்பம் செறிந்த வடிவங்களைத் துல்லியமாக விளக்கலாம், அலசலாம். இப்படத்தைக் வரைபடமாகத் தரும் சார்பு: cos(y arccos sin|x| + x arcsin cos|y|)

கணிதம்

கணிதம் அல்லது கணிதவியல் (ஒலிப்பு^ⓘ) (Mathematics) என்பது வணிகத்தில், எண்களுக்கு இடையான தொடர்பை அறிவதில், நிலத்தை அளப்பதில், அண்டவியல் நிகழ்வுகளை வருவதுரைப்பதில் மனிதனுக்கு இருந்த கணித்தலின் தேவைகள் காரணமாக எழுந்த ஓர் அறிவியல் பிரிவாகும். இந்த நான்கு தேவைகளும் பின்வரும் நான்கு பெரிய கணிதப் பிரிவுகளைப் பிரதிபடுத்துகின்றன:

• அளவு (quantity) – எண்கணிதம்
• அமைப்பு (structure) – இயற்கணிதம்
• பரவெளி (space) – வடிவவியல்
• மாற்றம் (change) – பகுவியல் (analysis) – நுண்கணிதம்

பல்வேறு கணிதவியலாளர்களுக்கும் இடையே கணிதத்தின் சரியான வீச்சையும் வரையறையையும் குறித்து பல்வேறு கருத்துக்கள் உள்ளன.

கணிதவியலாளர் தோரணங்களைத் தேடுகின்றனர்; கண்டுபிடித்த தோரணங்களைப் பயன்படுத்தி புதிய கணிப்புகளை உருவாக்குகின்றனர். தங்கள் கணிப்புகளின் மெய்,பொய் நிலைகளை கணித நிறுவல் மூலம் தீர்க்கின்றனர். உண்மை நிகழ்வுகளின் நல்ல முன்மாதிரிகளாக கணித அமைப்புக்கள் இருக்கும்போது கணித ஏரணங்கள் இயற்கை குறித்த புரிதலையும் முன்னறிவிதல்களையும் சாத்தியமாக்குகின்றது. எண்ணுதல், கணக்கிடுதல், அளவியல் இவற்றிலிருந்து நுண்கருத்துக்களையும் ஏரணத்தையும் பயன்படுத்தி கணிதம் முன்னேறியுள்ளது; பொருட்களின் வடிவங்களையும் இயக்கங்களையும் ஒழுங்குமுறையுடன் ஆராய்கின்றது. ஆவணங்கள் பதியப்பட்டபோதே செயல்முறைக் கணிதம் மாந்தச் செயற்பாடாக விளங்கியது. சில கணிதத் தீர்வுகளுக்கு பல ஆண்டுகள் அல்லது நூற்றாண்டுகள் தொடர்ந்த தேடுதல் நடந்துள்ளது.

கிரேக்க கணிதத்தில் கடுமையான கருத்தாய்வுகள் முதலில் தோன்றின; குறிப்பாக யூக்ளிடின் கூறுகளைக் கூறலாம். சூசெப்பெ பியானோ (1858–1932), டேவிடு இல்பேர்ட்டு (1862–1943) போன்றோரின் ஆக்கங்கள் மற்றும் பிற 19வது நூற்றாண்டு கணிதவியல் அமைப்புகளை அடுத்து ஏற்றுக்கொண்ட வரைவிலக்கணத்தின்படி கடுமையான கணித பகுத்தறிதல் மூலம் மெய்கோள்களின் உண்மையை நிறுவவதே கணித ஆராய்ச்சி என்ற கருத்து உருவானது. மறுமலர்ச்சிக் காலம் வரை மெல்லவே முன்னேறிய கணிதவியல் அறிவியல் கண்டுபிடிப்புகளின் இடைவினையால் கணித புத்தாக்கங்கள் மிக விரைவாக மேம்படத்தொடங்கின; இந்த விரைவான வளர்ச்சி இன்றுவரை தொடர்கின்றது.

கணிதம் இயற்கை அறிவியல், பொறியியல், மருத்துவம், நிதியியல், சமூக அறிவியல் போன்று உலகின் பல துறைகளில் முக்கியமானக் கருவியாகப் பயன்படுத்தப்படுகின்றது. கணிதத்தை மற்றத் துறைகளில் பயன்படுத்துவதைக் குறித்த பயன்பாட்டுக் கணிதம் புதிய அறிவியல் கண்டுபிடிப்புக்களைத் தூண்டவும் அவற்றைப் பயன்படுத்தவும் பயனாகின்றது. புள்ளியியல், ஆட்டக் கோட்பாடு போன்ற கணிதத்துறைகள் இவ்வாறு உருவானவையே. கணிதவியலாளர்கள் கணிதத்தைக் கொண்டு கணிதத்தை (தனிக் கணிதவியல்) அறியவும் முயல்கின்றனர். இந்தத் தனிக் கணிதத்தையும் பயன்பாட்டுக் கணிதத்தையும் பிரிக்கும் தெளிவான வரையறைகள் ஏதுமில்லை. தனிக்கணிதமாக துவங்கியவை பயன்பாட்டுக் கணிதமாக மாறுகின்றன.

வரையறை

கணிதம் (Math அல்லது Maths) இலக்கங்களும், அதன் செய்முறைகளும் (கூட்டல், கழித்தல், பெருக்கல், பிரித்தல்), அத்துடன் உருவ அமைப்புக்களும் (shapes) மட்டுமல்லாது விஞ்ஞான ஆராய்ச்சிகளுடனும், அதன் பிரயோகங்களுடனும் தொடர்ச்சியாக வளர்ந்து வரும் ஓர் அறிவியல் சாதனமாகும். கணிதத்தின் தேவை எமது அறிவியல் வளர்ச்சிக்கு ஒரு முக்கிய காரணியாகும். கலிலியோ "கணிதத்தின் உதவியால் நாம் இவ்வுலகத்தையே அறியலாம்" என்று கூறினார்.

எண்களை வைத்துக்கொண்டு உண்டாக்கப்பட்ட கணிப்பியலோ (arithmetic) வடிவங்களை வைத்துக்கொண்டு உண்டாக்கப்பட்ட வடிவியலோ இவைதான் கணிதவியல் என்று நினைப்போர் பலர். இன்னும் சிலர் எண்களுக்குப் பதிலாகக் குறிப்பீடுகளை வழங்கி அவைகளையும் எண்கள்போல் கணிப்புகள் செய்யும் இயற்கணிதம் தான் கணிதத்தின் முக்கிய பாகம் என்பர். மற்றும் சிலர் வடிவங்களை அலசி ஆராயும் வடிவியல் வளர்ச்சி தான் கணிதத்தின் இயல்பு என்று கூறுவர். ஆனால் கணிதம் இதையெல்லாம் தாண்டிய ஒன்று.

வரலாறு

தோற்றம்

முதன்மைக் கட்டுரை: கணித வரலாற்றின் காலக்கோடு

பித்தேகோரசு தேற்றத்தை கிரேக்க கணிதவியலாளர் பித்தாகரஸ் (கி மு அண். 570 – அண். 495) கண்டுபிடித்ததாக பொதுவாக கருதப்படுகின்றது.

தொடர்ந்து வளர்ந்த நுண்கருத்துக்களின் தொடராக கணிதம் உருவானது. பல விலங்குகளும் பகிரும் முதல் நுண்கருத்து எண்களாக இருக்கக் கூடும்: இரண்டு எண்ணிக்கை ஆப்பிள்களின் தொகுப்பும் இரண்டு எண்ணிக்கை மாம்பழங்களின் தொகுப்பும் ஏதோவொரு வகையில் பொதுவாக உள்ளன, அது அவற்றின் எண்ணிக்கை என்ற உணர்வாகும்.

தென் அமெரிக்காவில் இருந்த பழம் மாயா மக்களின் எண்முறை

எலும்புகளில் காணப்பட்ட கணக்கீடு குறிகளைக் கொண்டு, தொல் பழங்கால மக்கள் கட்புலனாகும் பொருட்களை எண்ணுவதை அறிந்திருந்ததுடன் நாட்கள், பருவ காலங்கள், ஆண்டுகள் போன்ற கட்புலனாகா அமைப்புக்களையும் எண்ணக் கற்றிருந்தனர் என அனுமானிக்கலாம்.

மிகச் சிக்கலான கணிதவியல் கி.மு.3000 வரை தோன்றவில்லை; அப்போதிலிருந்துதான் பபிலோனியர்கள், எகிப்தியர்கள் வரி மற்றும் பிற நிதிக் கணக்கீடுகள், கட்டிட மற்றும் கட்டுமானம், வானியல் போன்ற துறைகளில் எண்கணிதம், இயற்கணிதம், வடிவவியல் போன்றவற்றைப் பயன்படுத்தத் துவங்கினர். வணிகம், நில அளவியல், ஓவியக் கலை, நெசவுத் தோரணங்கள் மற்றும் நேரப் பதிகை ஆகியன கணிதத்தின் ஆரம்ப கால பயன்பாடுகளாக இருந்தன.

இந்தியக்கணித வரலாறு

முதன்மைக் கட்டுரை: இந்திய கணித அறிஞர்கள்

எண்ணும் எழுத்தும் இரண்டு கண்கள் போல என வள்ளுவர் கூறுகிறார். திருக்குறளில் ஒன்று, இரண்டு, மூன்று, நான்கு, ஐந்து, "அறு", "எழு", "எண்", பத்து, "கோடி" ஆகிய எண்கள் அல்லது தொகையீடுகள் அங்காங்கே பயன்படுத்தப்பட்டுள்ளன. எனினும் "தொண்டு" அல்லது "தொன்பது" பயன்படுத்தப்படவில்லை.

தமிழ் எண்ணுருக்கள், தமிழில் பூச்சியத்துக்கு குறியீடு இல்லை.[1]

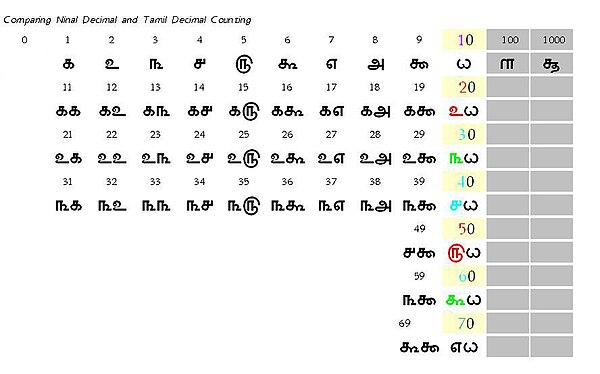
எண்களை எழுதுவதில் இடமதிப்புத் திட்டத்தையும் பூச்சியம் என்ற கருத்தையும் உருவாக்கி வருங்காலக் கணிதக் குறியீட்டுமுறைக்கு அடிகோலிட்டது பழையகால இந்தியா. இதைத்தவிர இந்தியக் கணிதவியலர்கள் (ஆரியபட்டர், பிரம்மகுப்தர், பாஸ்கராச்சாரியர், இன்னும் பலர்) மேற்கத்திய நாடுகள் மறுமலர்ச்சியடைந்து அறிவியலில் வளர்வதற்கு முன்னமேயே பலதுறைகளில் முன்னேற்றம் கண்டிருந்தனர்.

• வேதகாலத்துக்கணிதத்தின் கணிப்பு முறைகள்
• சுல்வசூத்திரங்களின் வடிவியல்
• சூனியமும் இடமதிப்புத் திட்டமும்
• எண்களின் அடிப்படைகளைப்பற்றி ஜைனர்கள்
• பாக்சாலி கையெழுத்துப்பிரதிகளின் சமன்பாடுகள்
• வானவியல்

இவையெல்லாம் இந்தியக்கணிதத்தின் சிறப்புகள்.

தற்காலத்திய கணிதத்தின் வரலாறு

14 வது நூற்றாண்டில் தொடங்கி, சென்ற ஆறு நூற்றாண்டுகளில் கணிதத்தின் வளர்ச்சியைத் தெரிந்துகொள்ள கணிதவியலாளர்கள் பலரின் வரலாறுகளே தக்க சான்றுகள். ஃபெர்மா, நியூட்டன், ஆய்லர், காசு, கால்வா, ரீமான், கோசி, ஏபல், வியர்சிற்றாசு, கெய்லி, கேன்ட்டர், இல்பட்டு, இப்படி இன்னும் நூற்றுக்கணக்கானவர்கள் பங்கு கொண்டு உருவாக்கப்பட்ட கணிதம் இன்றைய கணிதம்.

குறியீடு, மொழி, மற்றும் கடும்நெறி

இன்று பயன்படுத்தப்படும் பல கணிதவியல் குறியீடுகளை உருவாக்கி பரவலாக்கிய லியோனார்டு ஆய்லர்.

இன்று கணிதவியலில் பயன்படுத்தப்படும் பல குறியீடுகள் 16வது நூற்றாண்டு வரை கண்டுபிடிக்கப்படவில்லை. அதற்கு முன்னால் கணிதத்தை சொற்களால்தான் விவரித்தனர்; இது மிகவும் கடினமாகவும் புத்தாக்கங்களுக்குத் தடையாகவும் இருந்தது. இன்று பயன்படுத்தப்படும் பல குறியீடுகள் ஆய்லரால் (1707–1783) உருவாக்கப்பட்டவை. தற்காலக் குறியீடுகள் கணிதவியலாளர்களுக்கு கணிதத்தை எளிமையாக்கினாலும் புதியவர்களுக்கு கடினமாக உள்ளது. இவை மிகவும் சுருக்கப்பட்டவை; சில குறியீடுகள் அல்லது சின்னங்கள் நிரம்ப தகவலை உள்ளடக்கி உள்ளன. இசைக் குறியீடுகளைப் போலவே தற்கால கணிதக் குறியீடுகளுக்கும் கடுமையான இலக்கணங்கள் உள்ளன (ஆசிரியருக்கு ஆசிரியர் அல்லது துறைக்குத் துறை இவை சிறிதே வேறுபட்டிருக்கலாம்). இவற்றிலுள்ளத் தகவலை எழுத்தில் வடிப்பது என்பது மிகவும் கடினமாக இருக்கும்.

புதியவர்களுக்கு கணித மொழி மிகவும் கடினமானதாகத் தெரியலாம். அல்லது மற்றும் மட்டுமே போன்ற சொற்கள் வழக்குமொழியை விட மிகத் துல்லியமான பொருளைக் கொண்டவை. தவிரவும், சிலச் சொற்கள் சிறப்பானத் தனிப் பொருள் உடையன. கலைச்சொற்களான இடவியல் உருமாற்றம், தொகையீடு போன்றவற்றிற்கு கணிதத்தில் துல்லியமானப் பொருள் உண்டு. மேலும், சில சொல்லாடல்கள் iff for "if and only if" கணிதத்திற்கு மட்டுமேயானவை. சிறப்பு குறியீடுகளுக்கும் கலைச்சொற்களுக்கும் காரணம் உள்ளது: கணிதத்திற்கு வழக்குசொல்லாடலை விடத் துல்லியம் தேவைப்படுகின்றது. கணிதவியலாளர்கள் இந்தத் துல்லியமான மொழியையும் ஏரணத்தையும் கடும்நெறி (rigor) என்கின்றனர்.

கணிதவியல் புலங்கள்

கணிதத்தின் தற்காலப் புலங்களைப் பற்றிப் பட்டியலிடவேண்டுமானால் அப்பட்டியலில் 100 புலங்களுக்கும் மேலாக இருக்கும். இப்புலங்களுக்குள் மிகவும் வியப்பு தரும் உறவுகளும் உண்டு. இவைகளிலெல்லாம் கணிதத்திற்கென்றே தனித்துவம் வாய்ந்த மரபும் குறிப்பிடத்தக்கது. இம்மரபுதான் கணிதத்தை மற்ற அறிவியல் துறைகளிலிருந்து பிரித்துக் காட்டுகிறது.இவைதவிர, கணிதத்தின் அடிப்படைகளுக்கும் மற்ற துறைகளுக்குமான தொடர்பை ஏரணவியல் ஆய்கின்றது. மேலும் புள்ளியியல் போன்ற நேரடியாகப் பயன்படும் கணிதப் புலங்களும் உண்டு.

அளவு (Quantity)

• எண்கணிதம்
• அளவியல்

$1,2,3\,\!$	$-2,-1,0,1,2\,\!$	$-2,{\frac {2}{3}},1.21\,\!$	$-e,{\sqrt {2}},3,\pi \,\!$	$2,i,-2+3i,2e^{i{\frac {4\pi }{3}}}\,\!$
இயல்பெண்கள்	முழு எண்கள்	விகிதமுறு எண்கள்	மெய்யெண்கள்	செறிவெண்கள்

அமைப்பு (Structure)

• இயற்கணிதம்

எண் கோட்பாடு	நுண்புல இயற்கணிதம்	குலக் கோட்பாடு (Group Theory)	Order theory

வெளி (Space)

வடிவவியல்	முக்கோணவியல்	வகையீட்டு வடிவவியல் (Differential geometry)	இடவியல்	பகுவல்

மாற்றம் (Change)

நுண்கணிதம்	திசையன் நுண்கணிதம்	வகையீட்டு சமன்பாடுகள்	இயங்கியல் அமைப்புகள் (Dynamical systems)	ஒழுங்கின்மை கோட்பாடு

கணித அடித்தளங்கள் (Foundations and philosophy)

$P\Rightarrow Q\,$
ஏரணவியல் (கணிதம்)	கணக் கோட்பாடு, கணம் (கணிதம்)	பகுப்புக் கோட்பாடு (Category theory)

இலக்கமியல் கணிதம் (Discrete mathematics)

${\begin{matrix}(1,2,3)&(1,3,2)\\(2,1,3)&(2,3,1)\\(3,1,2)&(3,2,1)\end{matrix}}$
சேர்வியல்	கணிமைக் கோட்பாடு	வரைவியல் (Cryptography)	கோலக்கோட்பாடு (Graph theory)

கணிதக்கட்டுரை விமரிசனங்கள்

கணித விமரிசனங்கள் (Mathematical Reviews) என்ற ஒரு பத்திரிகை 1940 இல் ஒரு சில பக்கங்களுடன் தொடங்கி ஒவ்வொருமாதமும் கணிதத்தில் எழுதப்படும் புது ஆய்வுக்கட்டுரைகளை விமரிசிக்கவென்றே ஏற்படுத்தப்பட்டது. அது இன்று மாதத்திற்கு 2000 பக்கங்கள் கொண்டதாக வளர்ந்து, ஆயிரக்கணக்கான ஆய்வுப்பத்திரிகைகளிலிருந்து ஏறக்குறைய இருபது லட்சம் கட்டுரைகளின் விமரிசனத்தைக் கணிதப் பொக்கிஷமாகக் காத்து வருகிறது.

மேலும் காண்க

• கணிதக் கலைச்சொற்கள் (ஆங்கில அகர வரிசையில்)
• கணித மரபு
• கணிதப் பிரிவுகளின் உறவுகள்
• கணித அமைப்பு
• கணிதத்தின் நிலைப்பிகள்
• கணித இயல் வகைப்பாடு

வெளி இணைப்புகள்

கணிதம் வலைவாசல்

• மணிக்கணிதம் (Abacus)
• இந்தியா – கேரளா – ஆண்டு 10 பாட புத்தகத்தின் இணையப் பிரதி – அருமையான நடை, விளக்கம்
• தமிழ் இணைய பல்கலைகழகத்தின் கணித கலைச்சொல் அகராதி பரணிடப்பட்டது 2006-12-16 at the வந்தவழி இயந்திரம்
• Chennai Mathematical Institute
• The Institute of Mathematical Sciences, Chennai