புள்ளியியல்
இக்கட்டுரை கூகுள் மொழிபெயர்ப்புக் கருவி மூலம் உருவாக்கப்பட்டது. இதனை உரை திருத்த உதவுங்கள். இக்கருவி மூலம்
கட்டுரை உருவாக்கும் திட்டம் தற்போது நிறுத்தப்பட்டுவிட்டது. இதனைப் பயன்படுத்தி இனி உருவாக்கப்படும் புதுக்கட்டுரைகளும் உள்ளடக்கங்களும் உடனடியாக நீக்கப்படும் |
புள்ளியியல் அல்லது புள்ளிவிபரவியல் என்பது, தரவுகளைச் சேகரிப்பு, ஒழுங்கமைப்பு, பகுப்பாய்வு, விளக்கம் என்பன குறித்த பாடத்துறை ஆகும். கள ஆய்வுகள், சோதனைகள் என்பவற்றின் வடிவமைப்புத் தொடர்பிலான தரவுச் சேகரிப்புத் திட்டமிடல் உட்பட மேற்குறித்தவற்றில் எல்லா சிறப்புகளையும் இத்துறை கையாள்கிறது.
புள்ளியியலில் உரிய பயிற்சி பெற்று அத்துறைசார் பணிகளில் ஈடுபடுபவர் புள்ளியியலாளர் எனப்படுவார். புள்ளியியலாளர்கள், புள்ளியியல் பகுப்பாய்வின் வெற்றிகரமான பயன்பாட்டுக்குத் தேவையான வழி முறைகள் குறித்து நல்ல அறிவு பெற்றவராக இருப்பார். இத்தகையவர்கள், பொதுவாகப் புள்ளியியலின் பல்வேறுபட்ட துறைகளுள் ஏதாவது ஒன்றிலோ பலவற்றிலோ பணிபுரிந்து பட்டறிவு பெற்றவர்களாகவும் இருப்பர்.
செயற்பரப்பு[தொகு]
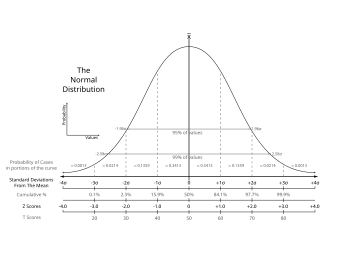
புள்ளி தகவல், புள்ளியியல் என்பன தரவுகளை சேகரித்தல், ஆராய்தல், பொருளை விளங்கவைத்தல் அல்லது விவரித்தல் மற்றும் தரவுகளை அளித்தல்[1] போன்றவை அடங்கிய கணிதம் சார்ந்த அறிவியலாக[2] சிலர் கருதுகிறார்கள் மற்றும் சிலர் அதனை தரவுகளை சேகரித்து அதன் பொருளை புரிந்துகொள்ளும் கணிதத்தின் ஒரு கிளையாக கருதுகின்றனர்.[3] புள்ளியியல் வல்லுனர்கள் சோதனைகளை வடிவமைத்து மற்றும் எடுத்துக்காட்டு மதிப்பீடுகள் மூலம் தரவுகளின் தரத்தை மேம்படுத்துகிறார்கள் தரவுகள் மற்றும் புள்ளியியல் எடுத்துக்காட்டடகளை பயன்படுத்தி எதிர்கால விளைவுகளை கணிக்கவும் மற்றும் எதிர்காலத்தை பகுப்பாய்வு செய்யவும் புள்ளியியல் ஒரு கருவியாக பயன்படுகிறது. புள்ளியியல் பலதரப்பட்ட துறைகளில் பயன்படுகிறது, கல்வி சார்ந்த துறைகளில், இயற்கை மற்றும் சமுதாய அறிவியல், அரசு, மற்றும் தொழில் அல்லது வணிகம் போன்றவை அடங்கும்.
புள்ளி தகவல் முறைகளை கொண்டு தரவுகளின் சேகரிப்பை தொகுத்து அளிக்க இயலும்: இதனை விளக்கமான புள்ளிவிபர முறை என்று அழைக்கின்றனர். ஆய்வுகளின் தீர்வுகளை வெளிப்படுத்த, இந்த முறை ஆராய்ச்சிகளில் மிகவும் பயன்படுத்தப்படுகிறது. கூடுதலாக, தன் போக்கிலமைந்த மற்றும் சமவாய்ப்புள்ள நிலையிலான மாறும் நிலையில்லா வகையிலான தரவுகளில் உருப்படிமங்களை முன்மாதிரியாக வைத்து கண்கானித்து, மற்றும் அதிலிருந்து அதன் செய்முறை அல்லது அதன் இனத்தொகையை ஆராய்ந்து கணிப்பதை; அனுமான புள்ளியியல் என அறியப்படுகிறது. அறிவியற் பூர்வமாக முன்னேற்றம் அடைய அனுமானம் ஒரு தலைமை அங்கமாகும், ஏன் என்றால் ஒரு தத்துவம் தர்க்க பூர்வமாக எங்கு செல்லும் என்பதை முன்கூட்டியே அறிய (தரவுகளின் அடிப்படையில்) அது வழிவகுக்கிறது. வழிகாட்டும் தத்துவத்தை நிரூபிக்க, இவ்வகையான கணிப்புகளை சோதித்தும் பார்ப்பதுண்டு, அப்படி செய்வது அறிவியல் முறைகளின் ஒரு பங்காகும். நினைத்தல் உண்மையாக இருந்தால், அப்போது புதிய தரவுகளின் விளக்கமான புள்ளி தகவல்கள் அது அந்த கருதுகோளின் வலுவான தன்மையை எடுத்துக்காட்டுகிறது. விளக்கமான புள்ளியியல் மற்றும் உய்த்துணர் புள்ளியியல் (யூகிக்கும் புள்ளி தகவல்கள் என்றும் அறியப்படுவது) இவை எல்லாம் சேர்ந்து செயல்முறை சார்ந்த புள்ளியியல் அல்லது புள்ளி தகவல்கள்[4] என அறியப்படுகிறது.
இதைத்தவிர கணிதம் சார்புடைய புள்ளியியல் என்ற ஒரு பிரிவும் உள்ளது, அது தலைப்பின் கொள்கைகளின் அடிப்படையைப் அறிந்துகொள்ள உதவும்.
ஆங்கிலத்து சொல்லான statistics ஒருமையிலோ அல்லது பன்மையிலோ பயன்படுத்தலாம்.[5] அதன் ஒருமை வடிவம், statistics இந்த தொகுப்பில் உரைக்கப்பட்ட கணித அறிவியலைக் குறிக்கும். பன்மை வடிவில், statistics அதாவது statistic என்ற ஒருமைச் சொல்லின் பன்மை வடிவம், ஒரு அளவை குறிப்பதாகும் (அதாவது தரவுகளை கணித்துப்பெறும் நடுமட்டம்) என்ற அளவைக் குறிக்கும்.[6]
புள்ளியியல், நிகழ்தகவுக் கோட்பாட்டுடன் நெருங்கிய தொடர்பு உடையது. நிகழ்தகவுக் கோட்பாட்டில், மொத்தத் தொகையின் கொடுபொருட்களில் இருந்து தொடங்கி எடுத்துக்காட்டுகளோடு தொடர்பான நிகழ்தகவுகளை உய்த்தறிகின்றனர். ஆனால், புள்ளியியலில் இது எதிர்த் திசையில் நடை பெறுகிறது. இங்கே எடுத்துக்காட்டிலிருந்து துவங்கி முழு அளவின் கொடுபொருட்கள் உய்த்தறியப்படுகின்றன.
வரலாறு[தொகு]
சில அறிஞர்கள் புள்ளியியல் முதல் முதலாக 1663 ஆண்டில் தோன்றியதாக சுட்டிக்காட்டுகின்றனர், ஜான் கிரான்ட் என்பவர் அவ்வாண்டு நாச்சுரல் அண்ட் பொலிடிகல் ஓப்செர்வேசன்ஸ் அபான் தி பில்ஸ் ஒப் மோர்டாலிடி என்ற கட்டுரையை வெளியிட்டார்.[7] நாட்டின் மக்கள் தொகை மற்றும் பொருளாதார தேவைகளின் அடிப்படையில் முந்தைய சிந்தனையாளர்கள் நாட்டிற்கான கொள்கைகளை உருவாக்க நினைத்ததால், ஆங்கிலத்தில் தொடக்கத்தில் ஸ்டேட் - என்ற சொல்தோற்றத்திற்கு காரணமாக அமைந்தது. புள்ளியியல் என்ற பிரிவின் நோக்கெல்லை 19 ஆம் நூற்றாண்டில் மேலும் விரிவடைந்தது மேலும் பொதுவாக தரவுகளை சேகரிப்பது மற்றும் தரவுகளை ஆராய்ந்து பார்ப்பதையும் அத்துடன் இணைத்துக் கொண்டது. இன்று, புள்ளியியல் மிகவும் பரவலாக அரசு, தொழில் அல்லது வணிகம், இயற்கை அறிவியல் மற்றும் சமூக அறிவியல் போன்ற துறைகளில் பயன்பட்டு வருகிறது.
அனுபவபூர்வமான ஆதாரங்களை அடிப்படையாக கொண்டதாலும், மற்றும் அதன் குவிமையம் பயன்பாட்டில் வேரூன்றியதாலும், புள்ளியியல் என்பது கணிதத்தின் ஒரு கிளையாக அல்லாமல், பொதுவாக ஒரு தனிப்பட்ட கணித அறிவியலாக கருதலாம்.[8][9] 17 ஆம் நூற்றாண்டில் பிளைஸ் பாஸ்கல் மற்றும் பிஎர்ரே தே பெர்மாத் ஆகிய இருவரும் நிகழ்ச்சித்தகவு கொள்கை என்ற பகுப்பை மேலும் மேம்படுத்தினார்கள் மற்றும் அதனுடைய கணிதத்திற்குரிய அடித்தளத்தையும் அமைத்தார்கள். நிகழ்ச்சித்தகவு கொள்கை என்ற பிரிவானது வாய்ப்புகளுக்கான விளையாட்டுக்களை பயிலும் போது ஏற்பட்டது. முதன் முதலாக குறைந்த வர்க்க முறை (method of least squares) கார்ல் பிரீட்ரிச் காஸ் (Carl Friedrich Gauss) என்பவர் 1794 ஆண்டுகளில் விவரித்தார். இன்றைய நவீன கணினிகளின் பயன்பாடு மிகையான அளவிலான புள்ளிவிவரங்கள் சார்ந்த கணக்கிடுதல் முறைகளை துரிதப்படுத்தியுள்ளது மேலும் மனிதனால் இயலாத சில புதிய முறைகளை செயல்படுத்தவும் அதன் மூலம் சாத்தியமாகி உள்ளது.
தி அமெரிக்கன் ஸ்டட்டடிக்கல் அசோசியேஷன் (American Statistical Association) என்ற அமைப்பு டெமிங் (Deming), பிஷேர் (Fisher), மற்றும் சி ஆர் ராவ் (CR Rao) போன்றவர்களை எக்காலத்தையும் சார்ந்த மிகவும் மகத்தான புள்ளியியல் வல்லுனர்களாக தரவரிசைப்படுத்தியுள்ளது.[10]
மீள்பார்வை[தொகு]
புள்ளியியல் முறைகளை அறிவியல், தொழில் அல்லது சமூகம் சார்ந்த பிரச்சினைகளுக்கு பயன்படுத்தும்போது, அதனை மக்கள்தொகை (கூட்டுத்தொகை) அல்லது வழிப்படுத்துதலை முதலில் வைத்துக்கொண்டு துவங்குவது பயில்வதற்கு முக்கியமாகும். மக்கள் தொகை அல்லது கூட்டுத்தொகை என்பது "ஒரு நாட்டில் வசிக்கும் அனைத்து மக்கள்" போன்றதோ அல்லது "ஒரு படிகத்தை சார்ந்த ஒவ்வொரு அணு" வாகவோ வேறுபட்டு இருக்கலாம். ஒரு கூட்டுத்தொகையானது ஒரு வழிபடுத்துதலுக்கான வெவ்வேறு நேரங்களில் எடுத்த பல அவதானிப்புகள் கொண்டவையாக இருக்கலாம், ஒவ்வொரு அவதானிப்பிலும் கிடைத்த தரவு மொத்த குழுமத்தில் ஒரு தனிப்பட்ட அங்கமாக இருக்கலாம். இவ்வகை "கூட்டுத்தொகை"யில் இருந்து சேகரித்த தரவு காலத்தொடர் வரிசை எனப்படும் முறையை சார்ந்ததாகும்.
நடைமுறை காரணங்களுக்காக, மொத்த குழுவையும் சார்ந்த தரவுகளை பயன்படுத்துவதற்கெதிராக (இந்த நடவடிக்கையை மக்கள் தொகைக்கணக்கு என்பார்கள்) - கூட்டுத்தொகையில் இருந்து தெரிவுசெய்த ஒரு மாதிரி பயன்படுகிறது. பயன்படும் கூட்டுத்தொகையை பிரதிநிதியாகக்கொண்ட ஒரு மாதிரி வரையறுத்ததும், அவ்வகை மாதிரி அங்கங்களிடமிருந்து ஒரு நோக்குதற்குரிய அமைப்பிலோ அல்லது சோதனைக்குரிய அமைப்பிலோ இருந்து தரவுகள் சேகரிக்கலாம். இந்தத்தரவு பிறகு புள்ளியியல் ஆய்விற்கு உள்ளாக்கப்படும், அவை இரு தொடர்புள்ள காரணங்களுக்கு பயன்படும்; விரித்துரைப்பு (விவரணம்) மற்றும் உய்த்துணர்வு.
- விரித்துரைப்பு புள்ளியியல் மாதிரிகளை ஆராய்ந்ததில் தெரியவந்ததை எண்ணளவில் அல்லது வரைபட அமைப்பு மூலமாக கூட்டுத்தொகை பற்றிய விவரங்கள் சுருக்கப்படுகின்றன. எண்ணளவிலுள்ள விவரிப்புகளில் நடுமட்டம் மற்றும் தரவிலக்கம், (திட்ட விலக்கம்) போன்றவை தொடர்ந்து வரக்கூடிய தரவு வகைகளுக்கும் (உயரம், எடை போன்றவை), அதே நேரத்தில் அலைவெண் மற்றும் விழுக்காடு கணக்கு போன்ற ஆணித்தரமான தரவுகளை (ஓட்டப்பந்தயம் போன்ற) விவரிக்க மிகவும் பயனுள்ளதாக காணப்படுகின்றன.
- உய்த்துணர்வு புள்ளியியல் உருப்படிமங்களை மாதிரி தரவுகளில் பயன்படுத்தி கூட்டுத்தொகையைப்பற்றிய உய்த்துணர்வுகளை அறிந்திட பயன்படுத்தப்படுகின்றன, அவை சீரற்ற இயல்பினை பிரதிநிதியாக கொண்டவையாகும். இவ்வகையான உய்த்துணர்வுகள் கிழே கொடுக்கப்பட்டுள்ள வடிவங்களை எடுக்கலாம்: தரவுகள் குறித்த ஆம்/இல்லை பதில்களை கொண்ட கேள்விகள் (எடுகோள் சோதனை) (hypothesis testing) தரவுகளின் எண்ணுக்குரிய சிறப்பியல்புகளை மதிப்பிடுதல் (எண் கணிப்பு) (estimation), தரவுகளில் காணப்படும் கூட்டாளிகளை விவரித்தல் (இயைபுப்படுத்தல்) (correlation), தரவுகளுக்கிடையே காணப்படும் மாதிரி உறவுகளை கண்டறிதல் (தொடர்புப்போக்கு) (regression), புறமதிப்பிடல் (extrapolation), இடைச்செருகல் (interpolation), அல்லது இதர மாதிரியமைத்தல் (modeling) இயல் நுட்பக்கூறுகள் (techniques) அநோவா (ANOVA), காலத்தொடர் வரிசை (time series), மற்றும் தரவுகளை சுரண்டி எடுத்தல் (data mining).
“... it is only the manipulation of uncertainty that interests us. We are not concerned with the matter that is uncertain. Thus we do not study the mechanism of rain; only whether it will rain.”
Dennis Lindley, "The Philosophy of Statistics", The Statistician (2000).
இயைபுப்படுத்தல் எனும் கருத்துப்படிவம் குழப்பத்தை ஏற்படுத்தக் கூடிய தன்மை கொண்டது என்பது குறிப்பிடத்தக்கதாகும். தரவு தொகுப்பு (data set) ஒன்றினை புள்ளிவிவர ஆய்விற்கு உட்படுத்தும்போது, கூட்டுத்தொகையின் இரு வேறுபட்ட குணங்கள் (properties) இணைந்து வேறுபடுவதாக காணலாம், ஏதோ அவர்களுக்கிடையே இணக்கம் இருப்பதுபோல. எடுத்துக்காட்டாக, வருடாந்தர வருவாய் பற்றிய ஆய்வறிக்கை ஒன்றில் இறந்தவர்களின் வயதுடன் கணக்கிடும் போது, பணக்காரர்களுக்கிடையே இருப்பதை விட, ஏழை மக்கள் குறைந்த வயதிலேயே இறந்து விடுவதாக காணப்படுவது. இவ்விரு மாறிகள் இயைபுப்படுத்தல் கொண்டவையாக கருதப்படுகின்றன; இருந்தாலும் அவை ஒன்றோடு ஒன்று நிகழ்வதற்கான காரணிகளாகவோ, அல்லாமலோ இருக்கலாம். இத்தகைய இயைபுப்படுதலுக்கான காரணம் ஒரு மூன்றாவதான, முன்பு கருதப்படாத ஒரு தோற்றப்பாடாக இருக்கலாம், அது ஒரு பதுங்கியிருக்கும் மாறியாக (lurking variable) இருக்கலாம் அல்லது ஒரு திகைப்பூட்டும் மாறியாக (confounding variable) இருக்கலாம். இக்காரணத்தினால், இவ்விரு மாறிகளுக்கிடையே ஒரு இயைபுப்படுத்தல் இருப்பதாக உடனுக்குடன் ஒரு காரணத்தொடர்பு உடையவையாக இருக்கும் என்று கூற இயலாது. (பாருங்கள் இயைபுப்படுத்தல் என்பது தூண்டு காரணமாக இருக்கலாம் என்று எண்ண இயலாது.)
ஒரு மாதிரி, முழு அளவின் ஒரு காட்டாக ஆவதற்கு, அது அதன் கூட்டுமொத்த அளவின் உண்மையான பிரதிநிதியாக இருத்தல் வேண்டும். ஒரு உண்மை பிரதிநிதியாக இருப்பது உறுதியானால், உய்த்துணர்வுகள் மற்றும் முடிவுகளை மாதிரிகளில் இருந்து முழு கூட்டுத்தொகைக்கு மொத்தமாக விரிவாக்கலாம். ஒரு தெரிவு செய்த மாதிரியானது எந்த அளவிற்கு உண்மையான பிரதிநிதியாக இருக்கும் என்பதை முடிவு செய்வது ஒரு பெரிய பிரச்சினையாகும். புள்ளியியல் மூலமாக ஒரு மாதிரிக்குள் ஏதேனும் இயைபிலா போக்கினை திருத்தவோ, மதிப்பீடு செய்வதற்கோ இயலும் மற்றும் தரவுகளை சேகரிக்கும் முறையையும் சரிசெய்யும். ஒரு பயில்வின் தொடக்கத்திலேயே இது போன்ற விவகாரங்களை குறைத்திடும் வகையான சோதனைகளை வடிவமைக்கவும் இயலும், அதன் மூலமாக அதன் கூட்டுத்தொகையின் உண்மை நிலவரத்தை அறிந்து கொள்ளும் திறமையை மேலும் வலுவடைகின்றது. புள்ளியியல் வல்லுனர்கள் வலுவான முறைகளை "கம்பீரமானவை" என கருதுகின்றனர்.(செய்முறைத் திட்டத்தைபார்க்கவும்.)
சீரற்ற இயல்புகளை புரிந்துகொள்வதற்கான கணித கருத்துப்படிவம் ஊக அளவை ஆகும். கணித புள்ளியியல் புள்ளியியல் கோட்பாடு எனவும் அறியப்படுவது, இது பயன்பாட்டுக் கணிதத்தின் கிளையாகும், இது ஊக அளவை கோட்பாடு மற்றும் பகுப்பாய்வு போன்றவைகளுடன் புள்ளியியலின் அறிமுறை அடிப்படையை சோதிக்க பயன்படுகிறது. எந்த முறையான புள்ளிவிபரமுறை பயன்பாட்டிற்கும் அதன் மக்கள்தொகை அல்லது கூட்டுத்தொகையானது அந்த முறையின் கணிதமுறையிலான அனுமானங்களுடன் ஒத்துப்போக வேண்டும், அப்போது தான் அவை ஏற்றுக்கொள்ளத்தக்கதாக இருக்கும்.
புள்ளியியல் முறைகளை தவறுதலாக பயன்படுத்தினால், அப்போது நேர்த்தியான மற்றும் கடுமையான பிழைகள் மற்றும் அதன் பொருள் விளக்கம் பிழைவடையும்- நேர்த்தியானது என்பது ஏன் என்றால் அனுபவம் வாய்ந்த வல்லுனர்கள் கூட இது போன்ற தவறுகளை செய்வார்கள், மற்றும் கடுமையான என்பது அதன் காரணமாக சூறையாடும் வகையான தவறுதலான முடிவுகள் எடுப்பதற்கு காரணமாகலாம் என்பதே ஆகும். எடுத்துக்காட்டாக, சமூகக் கொள்கை, மருத்துவ பயிற்சி மற்றும் பாலங்கள் போன்ற அமைப்புகளின் நம்பகம் யாவும் புள்ளியியலின் சரியான பயன்பாட்டை பொறுத்து இருப்பதேயாகும். புள்ளியியல் சரியாக பயன்பட்டு இருந்தாலும், சரியான தேர்ச்சி இல்லாதவர்களால் முடிவுகளை சரியான விதத்தில் பொருள் விளக்கம் செய்து கொள்ள இயலாது. தரவுகளில் காணப்படும் புள்ளிவிவர முறைப்பொருளுடைய தனிச்சிறப்புடன் கூடிய போக்கு - மாதிரியில் எந்த அளவுக்கு இயைபிலா மாறுபாடுகள் காரணமாக போக்குகள் பாதிக்கப்படுவது- அதனுடைய ஒரு உள்ளுணர்வு அளிக்கும் தனிமுறைச்சிறப்புடன் ஒத்துபோகலாம் அல்லது போகாமலும் இருக்கலாம். பொது மக்கள் தமது அன்றாட வாழ்க்கையில் தெரிந்து வைத்துக்கொள்ள வேண்டிய அடிப்படையான புள்ளியியல் திறமைகள் (மற்றும் சந்தேகம்) போன்றவைகளை புள்ளியியல் எழுத்தறிவு என்று அறியப்படுகிறது.
புள்ளியியல் முறைகள்[தொகு]
சோதனை மற்றும் நோக்குதற்குரிய ஆராய்ச்சிகள்[தொகு]
புள்ளியியல் சார்ந்த ஆராய்ச்சித்திட்டத்தின் பொதுவான குறிக்கோளானது காரணமாகச் செயல்படுதலுக்கான காரணத்தை கண்டுபிடித்தல், மற்றும் குறிப்பாக முன்கூற்றுகள் அல்லது சார்பற்ற மாறிகளில்ஏற்பட்ட மாறுதல்கள் காரணமாக சார்புடைய மாறிகளில் மாற்றங்கள் அல்லது பதில்களை கொண்டு முடிவுகளை எடுப்பதே. இரு பெரும்வகையான காரண புள்ளிவிபர ஆய்வுகளை / ஆராய்ச்சிகளை மேற்கொள்ள இயலும், அவை: சோதனைகளுடன் கூடிய ஆராய்ச்சிகள் மற்றும் நோக்குதற்குரிய ஆராய்ச்சிகள். இரு ஆராய்ச்சிமுறைகளிலும், ஒரு சார்பற்ற மாறியில் (அல்லது மாறிகளில்) ஏற்படும் வேறுபாடுகள் இன்னொரு சார்புடைய மாறியின் நடத்தையை எவ்வாறு பாதிக்கின்றது என்பது கண்டறியப்படுகிறது. இவ்விரு முறைகளிலும் உள்ள வேறுபாடுகள் இந்த ஆய்வு நடைமுறையில் செய்முறைப் படுத்தியதைப் பொறுத்தே இருக்கும். ஒவ்வொன்றும் பயனுள்ளதாகவே இருக்கும்.
ஒரு சோதனை ஆராய்ச்சி என்பது ஆய்வுக்கு உட்பட்ட முறைகளின் அளவுகளை அளந்துபார்ப்பது மற்றும் அந்த ஆய்வு முறையை கையாள்வது, மற்றும் பின்னர் மீண்டும் அதே முறையில் அளவுகளை அளந்துபார்ப்பது, அதன் மூலம் கையாண்டதன் விளைவாக அளவுகளில் மாற்றங்கள் ஏற்பட்டுள்ளதா என்பதை அறிந்துகொள்வதாகும். இதற்கு எதிராக, நோக்குதற்குரிய ஆய்வுகளில் சோதனை மூலம் கையாளும் பாங்கு நடப்பதில்லை. பதிலாக, தரவுகளை சேகரித்து, மற்றும் அதன் மூலம் ஊகங்கள் மற்றும் பதில்களுக்கு இடையேயான இயைபுப்படுத்தல் தொடர்புகள் கண்டறியப்படுகிறது.
ஒரு நோக்குதற்குரிய ஆய்வின் பெயர்பெற்ற எடுத்துக்காட்டு ஹவ்தொர்ன் ஸ்டடி (Hawthorne study) யாகும், அதில் ஹவ்தொர்ன் என்ற இடத்தில் அமைந்த வெஸ்டேர்ன் எலெக்ட்ரிக் கம்பெனியின் ஆலையில் நிலவிய பணிபுரியும் சூழலை மாற்றியமைப்பதால் ஏற்படக்கூடிய விளைவுகளை ஆராய்ந்து பார்த்தது. ஆராய்ச்சியாளர்கள் பணிபுரியும் இடத்தில் நிலவிய ஒளியூட்டத்தை அதிகரிப்பதால் பூட்டல் பட்டறை பணியாளர்களின் உற்பத்தித்திறன் மேலும் கூடுமா என்பதை அறிய விழைந்தனர். ஆராய்ச்சியாளர்கள் முதலில் நிலவிய உற்பத்தித்திறனை அளந்து பார்த்தார்கள், பிறகு ஆலையின் ஒரு பகுதியில் ஒளியூட்டத்தின் அளவை மாற்றியமைத்தார்கள் மற்றும் இவ்வகை மாறுதல்களினால் உற்பத்தித்திறனில் ஏற்பட்ட மாறுதலை கண்காணித்தார்கள். இதனால் உற்பத்தித்திறன் மேம்பட்டதை அவர்கள் கண்டார்கள். (சோதனைக்கு உட்பட்ட இடங்களில்/ நிலைமைகளில்.) இருந்தாலும், இந்த ஆய்வினை இன்று திறனாய்வாளர்கள் மிகவும் கடுமையாக விமரிசனம் செய்கிறார்கள், ஏன் என்றால் சோதனைக்குட்பட்ட செயல்முறைகளில் ஏராளமான தவறுகள் இருந்தன, முக்கியமாக அதற்கான ஒரு தனி கட்டுப்பாட்டுக் குழு இல்லாமல் செயல்பட்டது மற்றும் குருட்டுத்தன்மை போன்றவையாகும். ஹவ்தொர்ன் எப்பெக்ட் என அறியப்படுவது என்னவென்றால் ஒரு விளைவு (இந்த நிகழ்வில், பணியாளர்களின் உற்பத்தித்திறன்) நோக்குதற்குரிய காரணங்களினாலேயே மேம்பாடு அடைந்தது என்பது குறிப்பிடத்தக்கது. ஹவ்தொர்ன் ஆய்வில் ஈடுபட்டவர்களின் உற்பத்தித்திறன் ஒளியூட்டத்தை மாற்றி அமைத்ததால் வந்ததல்ல, ஆனால் அவர்கள் கவனிப்புக்கு ஆளானார்கள் என்பதே மெய்யாகும்.[மேற்கோள் தேவை]
நோக்குதற்குரிய ஆய்வுகளின் இன்னுமொரு எடுத்துக்காட்டு புகை பிடிப்போர் மற்றும் நுரையீரல் புற்றுநோயாளிகளுக்கிடையே நிலவும் இயைபுப்படுத்தலை வெளிப்படுத்துவது ஆகும்.
இதுபோன்ற ஆய்வுகளில், நாம் ஆர்வம் கொண்டுள்ள ஒரு பொருளை தெரிந்தெடுத்து அதைப்பற்றிய ஆய்விற்காக ஒரு எடுத்துக்காட்டான முறையில் கருத்தாய்வு மூலம் தரவுகளை சேகரித்து மேலும் அதனை ஒட்டிய புள்ளிவிபர ஆய்வுகளை மேற்கொள்ள வேண்டும். இந்நிகழ்ச்சியைப் பொறுத்தவரை, ஆராய்ச்சியாளர்கள் புகை பிடிப்பவர்கள் மற்றும் புகை பிடிக்காதவர்களிடம் இருந்து தரவுகளை சேகரிப்பார்கள், ஒரு வேளை கட்டுப்பாட்டுடன்கூடிய- நிகழ்வு மூலமாக, மற்றும் அவற்றில் ஒவ்வொரு குழுவிலும் நுரையீரல் புற்றுநோயால் அவதிப்படும் நபர்களின் எண்ணிக்கை, ஆய்வின் மூலம் பதிவு செய்வார்கள்.
சோதனைகள்[தொகு]
சோதனை புரிவதற்கான அடிப்படைகொண்ட படிகள் இவ்வாறு அமைதல் வேண்டும்:
- ஆராய்ச்சியை திட்டமிடுவது, அதற்கான தகவல்களை எங்கிருந்து திரட்ட வேண்டும், ஆராய்ச்சி செய்வதற்கான தலைப்பினை தேர்ந்தெடுத்தல், மற்றும் செய்யப்போகும் ஆராய்ச்சி மற்றும் அணுகுமுறை குறித்த நன்னடத்தை நெறிகளை கருத்தில் கொண்டு செயல்படுவது போன்றவை அடங்கும்.
- சோதனைகளை வடிவமைப்பது, தெரிவுசெய்த மாதிரிமுறைகளை செறிவாக்குதல் மற்றும் சார்பற்ற மாறிகள் மற்றும் சார்புடைய மாறிகளுக்கு இடையேயான இடைவிளைவுகள் மீது கவனம் செலுத்துதல்.
- தேவையற்ற விவரங்களை தவிர்த்து மாதிரி மாறிகளுக்கிடையே பொதுவாக காணப்படும் சேகரித்து கவனிப்புகளை தொகுத்தல். (விளக்கமான முறை கொண்ட புள்ளியியல்)
- கவனம் செலுத்திய உலகத்தில் இருந்து கிடைத்த கவனிப்புகள் மூலம் திரட்டிய தகவல் எதை குறிக்கிறது என்பது பற்றி கருத்தொருமையுடன் கூடிய முடிவுகளை எடுத்தல். (புள்ளிவிவரங்களின் அடிப்படையிலான உய்த்துணர்வு)
- ஆய்வில் இருநது கிடைத்த முடிவுகளை ஆவணப்படுத்துதல் மற்றும் அவற்றை தொகுத்து காட்சி அளித்தல்
அளவை நிலைகள்[தொகு]
புள்ளியியல் சேகரிப்பில் நான்கு வகையிலான அளவைகள் உள்ளன அல்லது அளவை நிலைகள் உள்ளன:
- பெயரளவில் ஆனவை,
- வரிசையெண்ணுக்குரியவை,
- இடைவேளை, மற்றும்
- விகிதம்
புள்ளியியலுக்கான ஆராய்ச்சியில் அவற்றில் ஒவ்வொன்றிற்கும் வேறுபடும் அளவிலான பயன்பாடுகள் உண்டு. விகித அளவு முறைகளில் பூச்சியத்தின் அளவு தெளிவாக தனிப்பட்ட வகையில் அர்த்தமுள்ள மதிப்பீடு கொண்டதாகவும் மேலும் அதனுடன் சேர்ந்து இதர இடைவெளிகளைக் குறிக்கும் அளவுகளும் வரையறுக்கப்பட்டுள்ளன; இவற்றின் உதவியுடன் தரவுகளை ஆராய்வதற்கான மிகவும் வளைந்துகொடுக்கும் தன்மையுடைய இணக்கமுள்ள புள்ளியியல் முறைகள் மிகவும் பயனுடையதாக அமைகின்றன. இடைவெளிகளுக்கான அளவுகளில் அளவுகளுக்கு இடையேயான அளவீடுகள் முறையாக வரையறுக்கப்பட்டுள்ளது (எடுத்துக்காட்டாக ஐ க்யு அளவுகள் அல்லது வெப்பமானியில் உள்ள ஃபாரன்ஹீட்போன்ற அளவுகள்) வரிசையெண்ணுக்குரிய அளவுகளில், ஒன்றுக்குப்பின் ஒன்றாக வரும் அளவுகள் துல்லியமாக இல்லாவிட்டாலும், அதற்கான பெறுமதி மிகவும் அர்த்தமுள்ள வரிசைக்கிரமம் கொண்டதாகும். பெயரளவிலான அளவுகளில் அவற்றின் வரிசைக்கிரமம் அர்த்தமுள்ள பெறுமதிகள் கொண்டவையல்ல.
பெயரளவிலான மற்றும் வரிசையெண்ணுக்குரிய அளவுமுறைகள் எண்ணளவில் அளவிட இயலாததால், சிலநேரங்களில் அவற்றை இணைத்து ஆணித்தரமான மாறிகள் என அழைக்கின்றனர், ஆனால் விகிதம் மற்றும் இடைவெளி அளவுகள் கொண்டவை இரண்டும் சேர்ந்து அளவையியல் அல்லது தொடரியல் சார்ந்த மாறிகளாக, அவற்றின் எண்ணுக்குரிய இயல்புகள் காரணமாக, அறியப்படுகின்றன.
சில நன்கு-அறிந்த புள்ளியியல் சோதனைகள் மற்றும் செய்முறைகள் ஆனவை:
- மாறளவுப் பகுப்பாய்வு அநோவா (ANOVA)
- சி-ஸ்கொயர் சோதனை (Chi-square test)
- இயைபுப்படுத்தல், (உடன் தொடர்பு) (Correlation)
- காரணிப்பகுப்பாய்வு
- மன்–விட்னி யு (Mann–Whitney U)
- எடையுடன் கூடிய சராசரி விலகல் வர்க்கம் (MSWD)
- பியர்சன் பெருக்கு-திருப்புதிறன்-தொடர்புறு குணகம் (கெழு) (Pearson product-moment correlation coefficient
- தொடர்புப் போக்குப் பகுப்பாய்வு(Regression analysis)
- ச்பியர்மானின் மதிப்பிடத் தொடர்பு கெழு (குணகம்) (Spearman's rank correlation coefficient)
- ஸ்டூடெண்டின் t சோதனை (Student's t-test)
- காலத்தொடர் வரிசை பகுப்பாய்வு (Time series analysis)
மிகச்சிறப்பு வாய்ந்த துறைகள்[தொகு]
சில துறைகள் பயன்பாட்டுப் புள்ளியியல் ஆராய்ச்சிகளை பரவலாக மேற்கொள்வதால், அவற்றிற்கு மிகச்சிறப்பு வாய்ந்த பெயர்களும் உள்ளன. கீழே வழங்கிய துறைகள் அவற்றை சார்ந்தவை:
- உண்மையுரிமை அறிவியல்
- பயன்பாட்டுத் தகவல் பொருளாதாரம்
- உயிரிபுள்ளியியல்
- காலணி நூல் மற்றும் மாலுமிக்கத்தி மறு மாதிரிமுறை
- வணிகவியல் புள்ளியியல்
- வேதியியல் புள்ளியியல் (வேதியியல்சம்பந்தப்பட்ட தரவுகளுக்கான புள்ளியியல் ஆய்வு)
- தரவு பகுப்பாய்வு
- தரவுகளை சுரண்டி எடுத்தல் (புள்ளியியல் மற்றும் கோலப்பாங்குகளை அடையாளம் காணுதல் மூலமாக தரவுகளில் இருந்து அறிவாற்றலை கண்டெடுத்தல்)
- மக்கள்தொகையியல்
- பொருளாதாரப் புள்ளியியல் (எகோநோமேற்றிக்ஸ்)
- சக்தி புள்ளியியல்
(ஆற்றல் புள்ளியியல்)
- பொறியியற் புள்ளியியல்
- புறப்பரவியல்
- புவியியல் மற்றும் புவியியல் தகவல் அமைப்புப் பொறியியல், குறிப்பாக இடமகன்ற ஆய்வுகள்
- பிம்ப செயல்முறையியல்
- உளப்புள்ளியியல்
- ஏற்புடைமைப் பொறியியல்
- சமூக புள்ளியியல்
- புள்ளியியல் வகைப்பாடு
- எழுத்தறிவு புள்ளியியல்
- புள்ளியியல் மாதிரியமைத்தல்
- புள்ளியியல் ஆய்வுகள்
- கட்டமைத்த தரவுகளின் ஆய்வு (புள்ளியியல்)
- பிழைப்புத்திறனாய்வு
- அடிப்பந்தாட்டம் மற்றும் துடுப்பாட்டம் போன்ற விளையாட்டுகளுக்கான புள்ளியியல்
வணிகவியல் மற்றும் உற்பத்தித்துறையிலும் புள்ளியியல் ஒரு முக்கிய அடிப்படைக்கருவியாக விளங்குகிறது. அதை வைத்துக்கொண்டு அளவுமானிகளின் மாறுபடும் தன்மையை அறிந்துகொள்ளவும், செய்முறைகளை கட்டுப்படுத்தவும், (புள்ளியியல் செயல்முறை கட்டுப்பாடு போன்ற (SPC), தரவுகளை தொகுப்பதற்காகவும், மற்றும் தரவுகளை சார்ந்த முடிவுகளை எடுப்பதற்காகவும் பயன்படுகிறது. இதுபோன்ற பணிகளில், இது ஒரு முக்கியமான கருவியாகும், மற்றும் நம்பத்தகும் ஒரே கருவியாகவும் இது இருக்கலாம்.
புள்ளிவிவரங்களை மதிப்பிடும் முறை[தொகு]
20 ஆம் நூற்றாண்டின் இரண்டாவது அரைப்பகுதியின் துவக்கம் முதல் கணிக்கும் முறைகளில் ஏற்பட்டுள்ள விரைவான மற்றும் விடா உறுதி வாய்ந்த ஆற்றல் புள்ளிவிவர அறிவியல் வழக்கங்களில் மகத்தான தாக்கத்தை ஏற்படுத்தியுள்ளன. முந்தைய புள்ளிவிவர மாதிரிகள் அனைத்தும் நேரோட்ட செயலாக்கம் கொண்ட மாதிரிகள் ஆகும், ஆனால் வலிமையான கணினிகள், மற்றும் அதனுடன் இணைந்த ஆற்றல் மிகுந்த நெறிமுறைகள், காரணமாக நேர் போக்கற்ற மாதிரிகளை (எடுத்துக்காட்டு நரம்பு சார்ந்த வலையமைப்புகளில்) ஆர்வத்தை தூண்டியது மேலும் புதிய வகைகள் கண்டுபிடிக்கப்பட்டன, எடுத்துக்காட்டாக பொதுவான நேரிடை மாதிரிகளை மற்றும் பலவகைமட்டம் கொண்ட மாதிரிகள்.
மேம்பட்ட கணினி மூலம் கிடைத்த ஆற்றலால் கணினி- மிகையாக பயன்படுத்தக்கூடிய முறைகளான மறுமாதிரிகளின் பயன்பாட்டினை உயர்த்தியுள்ளது, அவற்றில் பல்வகை நிலை மாற்றம் அடங்கிய சோதனைகள், மற்றும் பூட்ஸ்ட்ரேப் (bootstrap), மற்றும் கிப்ஸ் சாம்ப்ளிங் முறைகள் போன்றவை பயேசியன் மாதிரிகளை (Bayesian models) மேலும் பயனுள்ளதாக மாற்றியுள்ளது. கணினி புரட்சி புள்ளியியலுக்கான எதிர்காலத்தை மேலும் "சோதனை" மற்றும் "அனுபவத்திற்குரிய" புள்ளியியலாக மேன்மையடைய வழிவகுக்கிறது. மிகுந்த எண்ணிக்கைகளில் பொதுவான மற்றும் சிறப்பு தகுதிகள் கொண்ட புள்ளியியலுக்கான மென்பொருட்கள் இப்போது கிடைக்கப்பெற்றுள்ளன.
தவறான பயனீடு[தொகு]
புள்ளியியல் அறிவாற்றலை வேண்டுமென்றே அடிக்கடி அதனை பயன்படுத்தும் வல்லுனர்கள் தவறாக பயன்படுத்துகிறார்கள் /0} என்ற எண்ணம் பொது மக்களிடையே மேலோங்கி வருகிறது மேலும் அவர்கள் தங்களுக்கு வேண்டிய முறைகளில் தரவுகளை பொருள் விளக்கம் செய்துகொள்கிறார்கள் என்ற கருத்தும் நிலவுகிறது. பெஞ்சமின் டிஸ்ரேலி என்பவர் கூறிய புகழ்பெற்ற வார்த்தைகள், "மூன்று விதங்களிலான புளுகுகள் உள்ளன: புளுகுகள், தெறுமொழிகொண்ட புளுகுகள், மற்றும் புள்ளியியல்." 1909 ஆம் ஆண்டில் ஹார்வர்ட் ப்ரெசிடென்ட் ஆன லாவ்ரென்ஸ் லோவெல் எழுதியது புள்ளியியல், "...கன்று இறைச்சியைப்போல, அதை யார் செய்தார்கள் என்பதைப் பொறுத்து அது நன்றாக இருக்கும், மற்றும் அதில் கலந்துள்ள பொருட்களைப்பற்றியும் உறுதியாக இருக்க வேண்டும்."
பல்வேறுபட்ட ஆராய்ச்சிகள் ஒன்றுக்கொன்று வேறுபட்டிருந்தால், மக்கள் அது போன்ற ஆராய்ச்சிகளில் நம்பிக்கையை இழந்துவிடுவார்கள். எடுத்துக்காட்டாக, ஒரு ஆய்வு ஒரு உணவுமுறை அல்லது செய்கை இரத்த அழுத்தத்தை அதிகரிப்பதாகவும், மேலும் இன்னொன்று இரத்த அழுத்தத்தை குறைப்பதாகவும் கூறலாம். இதுபோன்ற வேறுபாடுகள் சோதனை முறைகளில் நேர்த்தியான மாற்றங்கள் காரணமாக ஏற்படலாம், எடுத்துக்காட்டாக நோயாளிகளின் குழுவில் வேறுபாடு அல்லது ஆராய்ச்சிக்கான நெறிமுறைகள் மாறுபட்டிருக்கலாம், அவற்றை பொதுமக்களால் எளிதாக புரிந்துகொள்ள இயலாது. (ஊடக அறிக்கைகள் பொதுவாக இதுபோன்ற முக்கியமான தகவல்களை மொத்தமாக வழங்க தவறுகிறார்கள், அவை மிகவும் சிக்கல் கொண்டதாக இருப்பதால்.)
ஒரு குறிப்பிட்ட மாதிரியை தெரிவுசெய்தோ (அல்லது தவிர்ப்பதாலோ, அல்லது மாற்றியமைத்தோ), முடிவுகளை கையாளலாம். இதுபோன்ற கையாளுதல் தீயநோக்குடனோ அல்லது நேரற்றதாகவோ இருக்காது; அவற்றை ஆராய்ச்சியாளர் தற்செயலாக புரிந்திருக்கலாம். தரவுகளை சுருக்கி விளக்கும் வரைபடங்கள் கூட தவறானவையாக இருக்கலாம்.
உண்மையில், கருதுகோள் சோதனை முறையானது, பரவலாக பயன்பட்டாலும் மற்றும் சட்டப்படி அல்லது விதிமுறைகள் காரணமாக வரையறுக்கப்பட்டாலும், சூனிய எடுகோள் என்ற கருதுகோளை அவை மிகையாக சார்ந்து இருப்பது ஒருவனை கட்டாயப்படுத்தும் முறையில் அமைந்துள்ளது மேலும் பெரிய அளவிலான ஆராய்ச்சிகளில் காணப்படும் சிறிய வேறுபாடுகளின் முக்கியத்துவத்தை மிகைப்படுத்துவதாகவும் காணப்படுகிறது என்ற ஆழ்ந்த குற்றச்சாட்டுக்கள் கொண்டதாகும். புள்ளியியல் கருத்துகள் படி மிகவும் உயர்ந்த தனிமுறைச்சிறப்பு கொண்ட ஒரு வேறுபாடு நடைமுறையில் ஒரு சிறப்பும் இல்லாமல் போகலாம். (கருதுகோள் விமரிசனம் மற்றும் சூனிய எடுகோள் பற்றிய சர்ச்சையை பார்க்கவும்.)
இதற்கான ஒரு விடையானது p -மதிப்பீட்டிற்கு மிகையான முக்கியத்துவம் கொடுப்பதாகும், கூடவே கொடுக்கப்பட்ட தனிச்சிறப்பு அளவிற்கு கருதுகோள் ஏற்றுக்கொள்ளப்பட்டதா இல்லையா என்பதையும் அறிக்கையில் தெரிவிக்க வேண்டும். இருந்தாலும், p -மதிப்பீடானது, விளைவின் அளவை சுட்டிக்காட்டுவதில்லை. மற்றுமோர் மிகையாக பயன்படும் பொது முறையானது நம்பிக்கை இடைவெளி யை முறையே அறிவிப்பதாகும். இது போன்ற கணிப்புகள் (calculations கணக்கீடுகள்) கருதுகோள் சோதனை முறை அல்லது p -மதிப்பீடுகள் செய்யும் முறையை தழுவியதாக இருப்பினும், அவை விளைவின் அளவு மற்றும் அதை சுற்றியுள்ள நிலையின்மையை, இரண்டையும் விவரிப்பதாகும்.
கணிதம் அல்லது கலைத்துறை சார்ந்த புள்ளியியல்[தொகு]
மரபுவழி, அரைகுறை தரம் கொண்ட ஆராய்ச்சி முறையியல் மூலமாக புள்ளியியல் உய்த்துணர்வுகளை பெற்றுவந்தது மேலும் அது மிகையான அறிவியல் பாடங்களிலும் "கற்றுக்கொள்ள தேவைப்பட்டது." புள்ளியியல் உய்த்துணர்வுகள் இல்லா சூழ்நிலைகளில் பயன்பட தொடங்கியதும் இது மாறுதல் அடைந்துள்ளது. ஒரு காலத்தில் மிகவும் வெறுப்புடன் அணுகிய ஒரு பாடம், பட்டம் பெறுவதற்காகவே பல துறைகளில் பாடமாக நுழைக்கப் பெற்றது, இன்று உற்சாகத்துடன் வரவேற்கப்படுகிறது. துவக்கத்தில் சில கணித வல்லுனர்கள் புறகணித்த இந்த பாடம், இப்போது சில துறைகளில் இன்றியமையாத ஒரு ஆராய்ச்சி முறையியலாக கருதப்படுகிறது.
- எண்ணியலில், பரவல் சார்பாக உருவாக்கிய தரவுகளின் சிதறல் படங்கள் மீது புள்ளியியல் முறைகளை பயன்படுத்தி அடிப்படையான கோலங்களை கண்டறியலாம் மற்றும் அவற்றின் மூலமாக கருதுகோளுக்கு சென்றடையலாம்.
- புள்ளியியல் முறைகள் மூலமாக முன்கூட்டி சொல்லும் முறையான எதிர்காலத்தை உய்த்தறிதல், அத்துடன் ஓழுங்கின்மை கோட்பாடு மற்றும் பிராக்டல் வடிவவியல் மூன்றும் கலந்த பயன்பாட்டினால் மிகவும் அழகிய வேலைப்பாடுகளுடைய வீடியோ படங்களை உருவாக்கலாம்.
- ஜாக்சன் பொல்லாக் பயன்படுத்திய வழிப்படுத்துதல் கலை இயற்கையில் தோன்றும் அடிப்படை பட்டுவாடா முறைகளை கலைவண்ணத்துடன் கூடிய சோதனைகள் மூலமாக வெளிப்படுத்தியதேயாகும், கணினிகளின் வரவுடன், புள்ளியியல் முறைகள் மூலம் இது போன்ற இயற்கை உந்துதல் பெற்ற பட்டுவாடா முறைகளை செயல்படுத்தி, மேலும் அவற்றின் மூலமாக விதரண விதிமுறைகளை ஆராய்ந்து, சலனத்துடன் கூடிய வீடியோ படங்களை எடுத்து ஆராய வழிபிறந்துள்ளது.
- புள்ளியியலுக்கான முறைகளை பயனிலையுடன் செயல்திறக் கலையில் பயன்படும்போது, எடுத்துக்காட்டாக மார்கோவ் செய்முறை போன்ற சீட்டு வித்தைகளில், அது சில நேரங்களில் மட்டுமே பணி புரியும், அந்த நிகழ்வினை புள்ளியியல் முறைகளின் படி சரியாக யூகித்து (ஊகித்து) விடலாம்.
- புள்ளியியல் முறைகள் பயனிலையுடன் கலைகளை உருவாக்க பயன்படுத்தலாம், எடுத்துக்காட்டாக ஐயன்னிஸ் சேனகிஸ் (Iannis Xenakis) என்பவர் கண்டுபிடித்த புள்ளியியற் பொறிமுறை மூலமாக புள்ளியியல் அல்லது முதன்மூல இசையை செய்முறைப்படுத்தலாம், இவ்விசையானது ஆற்றுகை-ஏற்றது ஆகும். நாம் நினைத்தபடி இக்கலை எப்போதும் இசையை வெளிப்படுத்தாவிட்டாலும், அதனை ஒரு குறைந்த எல்லைக்குள் யூகத்தின் அடிப்படையில் புள்ளியியல் முறைகளில் நடக்க வைக்கலாம்.
மேலும் பார்க்க[தொகு]
|
|
தொடர்புடைய துறைகள்[தொகு]
- சமூக அறிவியல்
- அரசியல் அறிவியல்
- சமூகவியல்
- நேர்க்காட்சி வாதம்
- சமூக ஆராய்ச்சி
குறிப்புகள்[தொகு]
- ↑ மோசேஸ், லின்கோல்ன் ஈ. தின்க் அண்ட் எகஸ்ப்லைன் வித் ஸ்டாடிஸ்டிக்ஸ் (Think and Explain with statistics), ப. 1 - 3. அடிசன் -வேச்லே, 1986.
- ↑ ஹாய்ஸ், வில்லியம் லீ, ஸ்டாடிஸ்டிக்ஸ் போர் தி சோசியல் சைன்செஸ் (Statistics for the social sciences), ஹோல்ட், ரிநேஹர்ட் மற்றும் வின்ஸ்டன், 1973, ப.xii, ஐ எஸ் பி என் பன்னாட்டுத் தரப்புத்தக எண் 978-0-03-077945-9
- ↑ "ஸ்டாடிஸ்டிக்ஸ் அட் என்சைக்லோபிடியா ஒப் மாதெமாடிக்ஸ் (Statistics at Encyclopedia of Mathematics)". Archived from the original on 2009-10-25. பார்க்கப்பட்ட நாள் 2009-10-25.
- ↑ அன்டேர்சன், டி.ஆர்.; சுவீனி, டி.ஜே.; வில்லியம்ஸ், டி.ஏ. ஸ்டாடிஸ்டிக்ஸ்: கோன்செப்ட்ஸ் அண்ட் அப்ப்ளிகேசன்ஸ் (Statistics: Concepts and Applications), ப.5 - 9. வெஸ்ட் பப்ளிஷிங் கம்பெனி, 1986.
- ↑ "Statistics". Merriam-Webster Online Dictionary.
- ↑ "Statistic". Merriam-Webster Online Dictionary.
- ↑ வில்ல்கோக்ஸ், வால்ட்டர் (1938) தி பௌண்டர் ஒப் ஸ்டாடிஸ்டிக்ஸ் (The Founder of Statistics) . ரிவியூ ஒப் தி இன்டரநேசனல் ஸ்டாடிஸ்டிகல் இன்ஸ்டிடுட் 5(4):321-328.
- ↑ Moore, David (1992). "Teaching Statistics as a Respectable Subject". Statistics for the Twenty-First Century. Washington, DC: The Mathematical Association of America. பக். 14–25.
- ↑ Chance, Beth L.; Rossman, Allan J. (2005). "Preface". Investigating Statistical Concepts, Applications, and Methods. Duxbury Press. பன்னாட்டுத் தரப்புத்தக எண்:978-0495050643. http://www.rossmanchance.com/iscam/preface.pdf.
- ↑ "காப்பகப்படுத்தப்பட்ட நகல்". Archived from the original on 2016-03-03. பார்க்கப்பட்ட நாள் 2022-01-04.
இக்கட்டுரையைச் சரிபார்ப்பதற்காக மேலதிக மேற்கோள்கள் தேவைப்படுகின்றன. |
குறிப்புகள்[தொகு]
- Best, Joel (2001). Damned Lies and Statistics: Untangling Numbers from the Media, Politicians, and Activists. University of California Press. பன்னாட்டுத் தரப்புத்தக எண்:0-520-21978-3. https://archive.org/details/damnedliesstatis00best.
- Alain Desrosières (2004). The Politics of Large Numbers: A History of Statistical Reasoning. Trans. Camille Naish. Harvard University Press. பன்னாட்டுத் தரப்புத்தக எண்:0-674-68932-1.
- Ian Hacking (1990). The Taming of Chance. Cambridge University Press. பன்னாட்டுத் தரப்புத்தக எண்:0-521-38884-8. https://archive.org/details/isbn_9780521388849.
- Dennis Lindley (1985). Making Decisions (2nd ed. ). John Wiley & Sons. பன்னாட்டுத் தரப்புத்தக எண்:0-471-90808-8. https://archive.org/details/makingdecisions00dvli.
- Tijms, Henk (2004). Understanding Probability: Chance Rules in Everyday life. Cambridge University Press. பன்னாட்டுத் தரப்புத்தக எண்:0-521-83329-9. https://archive.org/details/understandingpro0000tijm.
வெளி இணைப்புகள்[தொகு]
![]() விக்சனரி விக்சனரி
விக்சனரி விக்சனரி
![]() நூல்கள் விக்கிநூல்
நூல்கள் விக்கிநூல்
![]() மேற்கோள் விக்கிமேற்கோள்
மேற்கோள் விக்கிமேற்கோள்
![]() மூலங்கள் விக்கிமூலம்
மூலங்கள் விக்கிமூலம்
![]() விக்கிபொது
விக்கிபொது
![]() செய்திகள் விக்கிசெய்தி
செய்திகள் விக்கிசெய்தி
உடன் செயலாக்க வணிகத்திற்குரியல்லாத பாடநூல்கள்[தொகு]
- "எ நியூ வியூ ஒப் ஸ்டாடிஸ்டிக்ஸ்" ("A New View of Statistics"), வில் ஜி. ஹோப்கின்ஸ்,எ உ டி பல்கலைகழகம்
- "என் ஐ எஸ் டி / செமடேக் ஈ-ஹேண்ட்புக் ஒப் ச்டாடிச்டிகள் மேதட்ஸ்" "NIST/SEMATECH e-Handbook of Statistical Methods",யு எஸ் நேசனல் இன்ஸ்டிட்யுட் போர் ச்டாண்டார்ட்ஸ் மற்றும் டெக்னாலஜி (U.S. National Institute of Standards) மற்றும் செமடேக் (SEMATECH)
- "ஆன்லைன் ஸ்டாடிஸ்டிக்ஸ்: அன் இண்டராக்டிவ் மல்டிமீடியா கோர்ஸ் ஒப் ஸ்டடி" ("Online Statistics: An Interactive Multimedia Course of study"), டேவிட் லேன், ஜோன் லு, கமில்லே பெரேஸ், எமிலி ஜிடேக், போன்றோர்.
- "தி லிட்டில் ஹேண்ட்புக் ஒப் ஸ்டாடிஸ்டிகல் ப்ராக்டிஸ்" ("The Little Handbook of Statistical Practice"), கேரர்ட் ஈ. டல்லால், Tufts பல்கலைக்கழகம்
- "ஸ்டாட்சொப்ட் எலேக்ற்றோனிக் டேக்ச்ட்புக்", ஸ்டாட்சொப்ட்
இதர வணிகத்திற்குரியல்லாதவள ஆதாரங்கள்[தொகு]
- புக் ஒப் ஒட்ட்ஸ், தி ஒட்ட்ஸ் ஒப் எவரிடே லைப்.(Book of Odds, The odds of everyday life)
- இலவச புள்ளியியல் (இலவச மற்றும் திறமூல மென்பொருள், தரவு மற்றும் தனிமுறைப் பயிற்சி) Free Statistics (free and open source software, data, and tutorials)
- ஊக அளவை வெப் (Probability Web) (கார்ல்டன் காலேஜ்)
- ஊக அளவை மற்றும் புள்ளியியல் பயிற்சி மற்றும் பயில்வதற்கான வள ஆதாரங்கள் (Resources for Teaching and Learning about Probability and Statistics) பரணிடப்பட்டது 2009-03-03 at the வந்தவழி இயந்திரம் (ஈ ஆர் ஐ சி (ERIC))
- ரைஸ் வெர்ச்சுவல் லேப் இன் ஸ்டாடிஸ்டிக்ஸ் (Rice Virtual Lab in Statistics) (ரைஸ் பல்கலைக்கழகம்)
- ஸ்டாடிஸ்டிகல் சைன்ஸ் வெப் (மெல்போர்ன் பல்கலைக்கழகம்)
- ஸ்டாடிஸ்டிக்ஸ் கால்குலேடர்ஸ் (Statistics Calculators)
- அப்ப்லைட் ஸ்டாடிஸ்டிக்ஸ் ஆப்லேட்ஸ்
மல்டிமீடியா[தொகு]
- Introduction to Probability and Statistics[தொடர்பிழந்த இணைப்பு] - Animated video tutorial from the Defense Acquisition University

