கனம் (கணிதம்)

y=x³ (0≤x≤25).

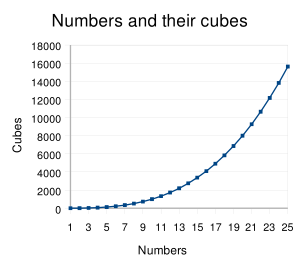
எண்கணிதம் மற்றும் இயற்கணிதம் இரண்டிலும் ஒரு எண்ணின் கனம் (ஒலிப்பு^ⓘ) (Cube) என்பது அந்த எண்ணின் மூன்றாம் அடுக்காகும். அதாவது அந்த எண்ணையே மூன்றுமுறை பெருக்கக் கிடைக்கும் எண்ணாகும்:

$n^{3}=n\times n\times n$

இந்த மதிப்பு, n அலகு பக்கங்கொண்ட ஒரு கனசதுரத்தின் கனஅளவாகும். இதிலிருந்துதான் இக்கருத்துருவிற்கு கனம் எனப் பெயரிடப்பட்டிருக்க வேண்டும்.

ஒரு எண்ணின் கனம் காணும் செயலுக்கு நேர்மாறுச் செயல் கனமூலம் காண்பது ஆகும். எந்த எண்ணை அந்த எண்ணாலேயே மூன்றுமுறை பெருக்க n கிடைக்குமோ அந்த எண் n -ன் கனமூலம் எனப்படும். ஒரு கனசதுரத்தின் கனஅளவு n எனில் n -ன் கனமூலம் அக்கனசதுரத்தின் பக்க அளவிற்குச் சமம்.

n -ன் கனமூலத்தின் குறியீடு:

${\sqrt[{3}]{n}}$ அல்லது n^1/3

ஒரு முழு எண்ணின் கனமானது முழுகனம் அல்லது கன எண் அல்லது கனசதுர எண் என அழைக்கப்படும். இவ்வெண்கள் வடிவ எண்களில் ஒரு வகையாகும்.

எதிர்மமல்லாத முழுகனங்களின் தொடர்வரிசை (OEIS-இல் வரிசை A000578)

0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744, 3375, 4096, 4913, 5832, 6859, 8000, 9261, 10648, 12167, 13824, 15625, 17576, 19683, 21952, 24389, 27000, 29791, 32768, 35937, 39304, 42875, 46656, 50653, 54872, 59319, 64000, 68921, 74088, 79507, 85184, 91125, 97336, 103823, 110592, 117649, 125000, 132651, 140608, 148877, 157464, 166375, 175616, 185193, 195112, 205379, 216000, 226981, 238328...

வடிவியல் முறையில் பார்த்தோமானால் m எண்ணிக்கை கொண்ட ஓரலகு திட கனசதுரங்களை ஒரு பெரிய கனசதுரத்துக்குள் சரியாக அடுக்க முடிந்தால், முடிந்தால் மட்டுமே m ஒரு கன எண்ணாக இருக்க முடியும் (m ஒரு நேர்ம எண்). எடுத்துக்காட்டாக , 27 சிறிய கனசதுரங்களை ஒரு பெரிய கன சதுரத்துக்குள் (ரூபிக்கின் கனசதுரம்) அடுக்க முடியும். ஏனென்றால்:

$27=3^{3}=3\times 3\times 3$

எதிர்ம முடிவிலியிலிருந்து நேர்ம முடிவிலி வரையுள்ள ஒவ்வொரு கன எண்ணின் அமைப்பு:

$n^{3}=(n-1)^{3}+3(n-1)n+1\,$

அல்லது

$n^{3}=(n+1)^{3}-3(n+1)n-1\,$

முதல் n கன எண்களின் கூடுதல் n -ஆம் வர்க்கப்படுத்தப்பட்ட முக்கோண எண்ணாகும்:

$1^{3}+2^{3}+\dots +n^{3}=(1+2+\dots +n)^{2}=\left({\frac {n(n+1)}{2}}\right)^{2}.$

எடுத்துக்காட்டாக முதல் ஐந்து கன எண்களின் கூடுதல் ஐந்தாவது முக்கோண எண்ணான 15 -ன் வர்க்கத்திற்குச் சமம்.

$1^{3}+2^{3}+3^{3}+4^{3}+5^{3}=15^{2}\,$

கூட்டுத்தொடரில் அமைந்த கன எண்களின் கூடுதல்

கூட்டுத்தொடரில் உள்ள கன எண்களின் கூடுதல் ஒரு கன எண்ணாக அமையும்

எடுத்துக்காட்டுகள்:

$3^{3}+4^{3}+5^{3}=6^{3}$

$11^{3}+12^{3}+13^{3}+14^{3}=20^{3}$

$31^{3}+33^{3}+35^{3}+37^{3}+39^{3}+41^{3}=66^{3}$

மேலுள்ள எடுத்துக்காட்டுக்களில் முதலாவது, பிளாட்டோவின் எண் எனப்படும்.

பொது வித்தியாசம் d மற்றும் முதல் உறுப்பு a³ கொண்ட n கன எண்களின் கூடுதல் காணும் வாய்ப்பாடு F  :

$F(d,a,n)=a^{3}+(a+d)^{3}+(a+2d)^{3}+...+(a+dn-d)^{3}\,$

$F(d,a,n)=(n/4)(2a-d+dn)(2a^{2}-2ad+2adn-d^{2}n+d^{2}n^{2})\,$

$F(d,a,n)=y^{3}\,$ -ன் தீர்வு:

• சிறப்பு வகையான d = 1 எனும் அடுத்தடுத்த கன எண்களுக்கு உள்ளது.
• ஆனால் d > 1 ஆக உள்ள முழு எண் மதிப்புகளுக்கு, ( d = {2,3,5,7,11,13,37,39,...}) இடையிடையே உள்ள தீர்வுகள் மட்டுமே காணப்பட்டுள்ளன.

வரலாறு

பண்டைக் காலத்தில் மிகவும் சாதாரணமாக பெரிய எண்களின் கனங்கள் காணப்பட்டன. பழங்கால இந்திய கணிதவியலாளர் ஆரியபட்டர் அவரது புகழ்பெற்ற படைப்பான ஆரியபட்டியத்தில் கன எண்ணைப் பற்றி விளக்கியுள்ளார் (ஆரியபட்டியம், 2-3): "மூன்று சமன்களின் தொடர் பெருக்கலும், அதைப்போலவே 12 சம விளிம்புகள் கொண்ட செவ்வக திடப்பொருளும் கனம் என அழைக்கப்படுகின்றன." இதைப்போன்ற வரையறைகளை பிரம்மபுத்தர் சித்தாந்தம் (XVIII. 42), கணித சார சங்கிரகா (II. 43) மற்றும் சித்தாந்த சேகரா (XIII. 4) ஆகியவற்றில் காணலாம். சமஸ்கிருத்தில் உள்ளது போலவே நவீனகால கணிதத்திலும் கனம் என்ற வார்த்தை இருவிதமான கணிதப்பொருளைத் தருவது குறிப்பிடத்தக்கது. சமஸ்கிருதத்தில், Ghhana என்ற வார்த்தை தனக்குத்தானே மூன்று முறை பெருக்கிக் கொள்ளப்படும் ஒரு எண்ணின் அடுக்குக்காரணியையும் மற்றும் ஒரு கனவடிவையும் குறிக்கும்.

மேற்கோள்கள்

• Hardy, G. H.; Wright, E. M. (1980). An Introduction to the Theory of Numbers (Fifth edition). Oxford: ஒக்ஸ்போர்ட் பல்கலைக்கழகப் பதிப்பகம். பன்னாட்டுத் தரப்புத்தக எண்:978-0198531715 

வெளி இணைப்புகள்

• A web application that decomposes an integer number not congruent to 4 or 5 (mod 9) into a sum of four cubes.