செவ்வகம்
| செவ்வகம் | |
|---|---|
 செவ்வகம் | |
| வகை | நாற்கரம், இணைகரம் |
| விளிம்புகள் மற்றும் உச்சிகள் | 4 |
| சிலாஃப்லி குறியீடு | { } × { } |
| கோஎக்சிட்டர்-டின்க்கின் படம் | |
| சமச்சீர் குலம் | Dih2, [2], (*22), வரிசை 4 |
| இருமப் பல்கோணம் | சாய்சதுரம் |
| பண்புகள் | குவிவு, சமகோணமுடையது, வட்ட நாற்கரம், எதிர் கோணங்களும் எதிர்ப் பக்கங்களும் சமம் |
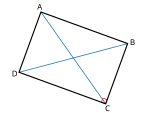
செவ்வகம் (Rectangle) என்பது யூக்ளிடிய தள வடிவியலின் அடிப்படை வடிவங்களில் ஒன்று. இது நான்கு செங்கோணங்களைக்கொண்ட ஒரு நாற்கரமாகும். சமகோண நாற்கரம் என்றும் இதனைக் கூறலாம். இதன் எதிர்ப் பக்கங்கள் சம நீளம் கொண்டவை; ஒவ்வொரு கோணமும் செங்கோணமாகும். இதனால் செவ்வகத்தின் எதிர்ப் பக்கங்கள் இணையானவை. எனவே இது இணைகரத்தின் ஒரு சிறப்பு வடிவமாகும். அதாவது செங்கோணமுடைய ஒரு இணைகரமாக இருக்கும். செவ்வகத்தின் மூலை விட்டங்கள் செங்கோணத்தில் ஒன்றையொன்று சம துண்டங்களாக வெட்டுகின்றன.
நான்கு பக்கங்களும் சமமாகவுள்ள செவ்வகமானது சதுரம் ஆகும். சதுரமாக அமையாத செவ்வகங்கள் சில சமயங்களில் நீள்சதுரம் என அழைக்கப்படுகின்றன[1][2][3] ஒரு செவ்வகத்தின் உச்சிகள் ABCD எனில், அது ABCD எனக் குறிக்கப்படும்.
இரண்டு எதிர்ப் பக்கங்கள் மற்றும் இரண்டு மூலைவிட்டங்களைக் கொண்டதாய்த் தன்னைத்தானே குறுக்காக வெட்டிக்கொள்ளும் நாற்கரமானது குறுக்குச் செவ்வகம் (crossed rectangle) என அழைக்கப்படும்[4]. குறுக்குச் செவ்வகமானது எதிர் இணைகரத்தின் ஒரு சிறப்புவகையாகும். மேலும் அதன் கோணங்கள் செங்கோணங்களாக இருக்காது, ஆனால் சமமானவையாக இருக்கும். கோள வடிவவியல், நீள்வட்ட வடிவியல், அதிபரவளைய வடிவவியல் போன்ற பிற வடிவவியல்களில் எதிர்ப் பக்கங்கள் சமமாகவும் செங்கோணமாக இல்லாமல் அதேசமயம் சமமாகவுள்ள கோணங்களையும் கொண்ட இத்தகைய செவ்வகங்கள் உள்ளன.
பண்புருக்கள்[தொகு]
ஒரு குவிவு நாற்கரத்திற்குப் பின்வரும் கூற்றுகளில் ஏதேனும் ஒன்று உண்மையாக இருந்தால் மட்டுமே, அந்நாற்கரம் செவ்வகமாக இருக்க முடியும்:[5][6]
- ஒரு சமகோண நாற்கரம்
- நான்கு செங்கோணங்கள் கொண்ட நாற்கரம்
- குறைந்தபட்சம் ஒரு செங்கோணம் கொண்ட இணைகரம்
- சமநீளமுள்ள மூலைவிட்டங்களைக் கொண்ட மூலைவிட்டம்
- ABD , DCA முக்கோணங்களைச் சர்வசமமாகக் கொண்ட இணைகரம் ABCD
- a, b, c, d அளவுகளை அடுத்தடுத்த பக்கநீளங்களாகவும், பரப்பளவும் கொண்ட குவிவு நாற்கரம்.[7]:fn.1
- a, b, c, d அளவுகளை அடுத்தடுத்த பக்கநீளங்களாகவும், பரப்பளவும் கொண்ட குவிவு நாற்கரம்.[7]
வகைப்பாடு[தொகு]

மரபுவழி அடுக்கமைப்பு[தொகு]
செவ்வகம், அடுத்தடுத்துள்ள ஒவ்வொரு சோடி பக்கமும் செங்குத்தாகவுள்ள ஒரு சிறப்புவகை இணைகரம்.
இணைகரம், இரு சோடி எதிர்ப் பக்கங்களும் இணையாகவும் சமநீளமானவையாகவும் கொண்ட ஒரு சிறப்புவகைச் சரிவகம்.
சரிவகம், குறைந்தபட்சம் ஒரு சோடி இணையான எதிர்ப்பக்கங்களைக் கொண்ட ஒரு சிறப்புவகை குவிவு நாற்கரம்.
குவிவு நாற்கரம்,
- ஒரு எளிய பல்கோணமாகும். அதன் வரம்புக்கோடு தன்னையே வெட்டிக்கொள்ளாது
- ஒரு விண்மீன் வடிவப் பல்கோணம். அதன் முழு உட்புறமும் எந்தப் பக்கத்தையும் குறுக்கிட்டுச் செல்லாமலேயே ஒரு புள்ளியிலிருந்து காணக்கூடியதாகும்.
மாற்று அடுக்கமைப்பு[தொகு]
ஒவ்வொரு சோடி எதிர் பக்கங்களின் வழியே எதிரொளிப்பு சமச்சீர் அச்சுக்களைக் கொண்ட நாற்கரமாக ஒரு செவ்வகம் வரையறுக்கப்படுகிறது.[8] இந்த வரையறைக்குள் செங்கோணச் செவ்வகங்களும் குறுக்குச் செவ்வகங்களும் அடங்கும். இவற்றுக்கு ஒரு சோடி எதிர் பக்கங்களிலிருந்து சமதூரத்திலும் இணையாகவும் உள்ள ஒரு சமச்சீர் அச்சும், அப்பக்கங்களுக்குச் நடுக்குத்துக்கோடாக அமையும் மற்றொரு சமச்சீர் அச்சும் இருக்கும். ஆனால் குறுக்குச் செவ்வகத்தில் முதல்வகை சமச்சீர் அச்சானது அது சமக்கூறிடும் இரு பக்கங்களுக்கும் சமச்சீர் அச்சாக இருக்காது.
ஒவ்வொரு சோடி எதிர் பக்கங்களின் வழியான இரு சமச்சீர் அச்சுகளைக் கொண்ட நாற்கரங்கள், ஒரு சோடி எதிர் பக்கங்களின் வழியாக குறைந்தபட்சம் ஒரு சமச்சீர் அச்சு கொண்ட நாற்கரங்களின் வகைக்குள் அடங்கும். இருசமபக்கச் சரிவகங்களும் இருசமபக்கக் குறுக்குச் சரிவகங்களும் இவ்வகையான நாற்கரங்களாகும்.
பண்புகள்[தொகு]
சமச்சீர்மை[தொகு]
- செவ்வகம் ஒரு வட்ட நாற்கரம்: செவ்வகத்தின் நான்கு உச்சிகளும் ஒரே வட்டத்தின் மீதமையும்.
- செவ்வகம் ஒரு சமகோண வடிவம்: செவ்வகத்தின் நான்கு கோணங்களும் சமம் (ஒவ்வொன்றும் 90 பாகைகள்).
- ஒரு செவ்வகம் இரு எதிரொளிப்பு சமச்சீர் அச்சுகளும், இரண்டாம் வரிசை சுழற்சி சமச்சீரும் (180° சுழற்சி) கொண்டது.
செவ்வகம்-சாய்சதுரம்[தொகு]
ஒரு செவ்வகத்தின் இரட்டைப் பல்கோணம் சாய்சதுரமாகும்.[9]
| செவ்வகம் | சாய்சதுரம் |
|---|---|
| எல்லாக் கோணங்களும் சமம். | எல்லாப் பக்கங்களும் சமம். |
| ஒன்றுவிட்ட பக்கங்கள் சமம். | ஒன்றுவிட்ட கோணங்கள் சமம். |
| உச்சிகளிலிருந்து அதன் மையம் சமதூரத்தில் அமையும். எனவே ஒரு சூழ்தொடு வட்டம் கொண்டிருக்கும். | பக்கங்களிலிருந்து சமதூரத்தில் மையம் அமையும். அதனால் உள்வட்டம் கொண்டிருக்கும். |
| சமச்சீர் அச்சுகள் எதிர்ப் பக்கங்களை இருசமக்கூறிடும். | சமச்சீர் அச்சுகள் எதிர்க் கோணங்களை இருசமக் கூறிடும். |
| மூலைவிட்டங்கள் சம நீளமுள்ளவை. | மூலைவிட்டங்கள் சமகோணத்தில் வெட்டிக்கொள்ளும். |
- செவ்வகத்தின் பக்கங்களின் நடுப்புள்ளிகளை வரிசைப்படி இணைக்கக் கிடைக்கும் வடிவம் சாய்சதுரமாகவும், சாய்சதுரத்தின் பக்கங்களின் நடுப்புள்ளிகளை வரிசைப்படி இணைக்கக் கிடைக்கும் வடிவம் செவ்வகமாகும் கிடைக்கும்.
பிற பண்புகள்[தொகு]
- இரு மூலைவிட்டங்களும் சமநீளமுள்ளவை; ஒன்றையொன்று இருசமக்கூறிடும். இவ்விரு பண்புகளுமுடைய நாற்கரங்கள் ஒவ்வொன்றும் ஒரு செவ்வகமாகும்.
- செவ்வகமொரு நேர்கோட்டுப் பல்கோணம். அதன் பக்கங்கள் செங்கோணத்தில் சந்திக்கின்றன.
- ஒன்றுக்குள் மற்றொன்று பொருந்தாத இரு செவ்வகங்கள் ஒப்பற்றவை எனப்படும்.
செவ்வகத்தின் பரப்பைக் கணித்தல்[தொகு]
ஒரு செவ்வகத்தின் பரப்பளவு அதன் நீளம் மற்றும் அகலம் ஆகியவற்றைப் பெருக்குவதால் கிடைக்கும். எடுத்துக்காட்டாக, ஒரு செவ்வகத்தின் நீளம் 6 மீட்டர் மற்றும் அகலம் 5 மீட்டர் எனில், அதன் பரப்பளவு 6 x 5 = 30 சதுர மீட்டர் ஆகும்.
சுற்றளவு, மூலை விட்டத்தின் நீளம்[தொகு]
AC, BD ஆகிய எதிர் எதிர் முனைகளை இணைக்கும் மூலை விட்டங்கள் கோணல் கோடுகள் இரண்டும் ஈடாக (சமமாக) இருக்கும். AC ஈடு BD. எனவே AC = BD.
ஒரு செவ்வகத்தின் அடுத்தடுத்த பக்கங்களின் நீளங்கள் a, b எனில், அதன் சுற்றளவு 2(a+b) ஆகும். மூலை விட்டத்தின் (கோணல் கோட்டின்) நீளம் √(a2+b2)
வாய்பாடுகள்[தொகு]

செவ்வகத்தின் நீளம் , அகலம் எனில்:
- செவ்வகத்தின் பரப்பளவு ,
- செவ்வகத்தின் சுற்றளவு ,
- ஒவ்வொரு மூலைவிட்டத்தின் நீளம் ,
- ஒரு செவ்வகத்தின் எனில் அச்செவ்வகம் ஒரு சதுரம் ஆகும்.
தேற்றங்கள்[தொகு]
- சமச்சுற்றளவுத் தேற்றத்தின்படி, ஒரேயளவு சுற்றளவு கொண்ட செவ்வகங்களுக்குள் மிகப்பெரிய பரப்பளவு கொண்டது சதுரமாகும்.
- ஒன்றுக்கொன்று செங்குத்தான மூலைவிட்டங்களைக் கொண்ட நாற்கரத்தின் பக்கங்களின் நடுப்புள்ளிகள் ஒரு செவ்வகத்தை உருவாக்கும்.
- சம மூலைவிட்டங்கள் கொண்ட இணைகரம் ஒரு செவ்வகமாகும்.
- வட்ட நாற்கரங்களின் ஜப்பானியத் தேற்றப்படி, ஒரு வட்ட நாற்கரத்தின் உச்சிகளைக் கொண்டு உருவாக்கப்படும் நான்கு முக்கோணங்களின் உள்வட்டங்கள் ஒரு செவ்வகத்தை அமைக்கும்.[10]
- பிரித்தானியக் கொடித் தேற்றப்படி, ABCD செவ்வகத்தின் தளத்திலமைந்த ஏதேனுமொரு புள்ளி P எனில்:[11]
- ஒரு தளத்திலமைந்த ஒரு குவிவு வடிவம் C எனில், அதனுள் வரையப்படும் செவ்வகம் r இன் ஒத்தநிலை வடிவம் R , C இன் சூழ்தொடு வடிவாகவும், ஒத்தநிலை விகிதம் அதிகபட்சம் 2 ஆகவும் இருக்கும். மேலும் .[12]
குறுக்குச் செவ்வகங்கள்[தொகு]

ஒரு செவ்வகத்தின் ஒன்றுக்கொன்று வெட்டிக்கொள்ளாத இரு எதிர்ப் பக்கங்களாலும் அச்செவ்வகத்தின் இரு மூலைவிட்டங்களாலும் ஆனது குறுக்குச் செவ்வகம். குறுக்குச் செவ்வகத்தின் உச்சிகளின் வரிசையமைப்பு, செவ்வகத்தின் உச்சிகளின் வரிசையாகவே இருக்கும். பொது உச்சியுடைய இரு ஒரேமாதிரியான முக்கோணங்களைக் கொண்டது போலத் தோற்றம் கொண்டிருக்கும். ஆனால் மூலைவிட்டங்கள் வெட்டிக்கொள்ளும் புள்ளி, குறுக்குச் செவ்வகத்தின் உச்சியாகாது.
குறுக்குச் செவ்வகம் சமகோணமுடையதல்ல. எல்லா குறுக்கு நாற்கரங்களுக்கும் உள்ளது போல, குறுக்குச் செவ்வகத்தின் நான்கு உட்கோணங்களின் கூடுதல் (இரு குறுங்கோணங்கள், இரு பின்வளைகோணங்கள்) 720°.[13]
செவ்வகம், குறுக்குச் செவ்வகத்தின் பொதுப் பண்புகள்:
- எதிர்ப் பக்கங்கள் சம நீளமானவை.
- இரு மூலைவிட்டங்கள் சமநீளமானவை.
- இரண்டுக்கும் இரண்டு எதிரொளிப்பு அச்சுகளும் இரண்டாம் வரிசை சுழற்சி சமச்சீர்மையும் (180° கோணச் சுழற்சி) உண்டு.
பிற செவ்வகங்கள்[தொகு]

கோள வடிவவியலில் கோளச் செவ்வகம் என்பது 90° க்கும் அதிகமான கோணத்தில் சந்திக்கும் நான்கு விளிம்புகளையும் பெரு வட்டங்களாகக் கொண்ட வடிவம் ஆகும். கோளச் செவ்வகத்தின் எதிர் விற்கள் சமமானவை.
நீள்வட்ட வடிவவியலில் நீள்வட்டச் செவ்வகம் என்பது ஒரு நீள்வட்டத் தளத்தில், 90° க்கும் அதிகமான கோணத்தில் சந்திக்கும் நான்கு நீள்வட்ட விற்களாலான வடிவம் ஆகும். இதன் எதிர் விற்கள் சமமானவையாக இருக்கும்.
அதிபரவளைய வடிவவியலில் அதிபரவளையச் செவ்வகம் என்பது ஒரு அதிபரவளையத் தளத்தில், 90° க்கும் குறைவான கோணத்தில் சந்திக்கும் நான்கு அதிபரவளைய விற்களாலான வடிவம் ஆகும். இதன் எதிர் விற்கள் சமமானவையாக இருக்கும்.
தரைபாவுமைகள்[தொகு]
பல தரைபாவுமைகளில் (tessellation) செவ்வகங்கள் பயன்படுகின்றன.
எடுத்துக்காட்டுகள்:
 அடுக்கு இணைப்பு |
 தொடர் கல் இணைப்பு |
 கூடை நெசவு |
 கூடை நெசவு |
 மீன்முள்வடிவ குறுக்கீட்டு விளைவுரு |
மேலும் பார்க்க[தொகு]
மேற்கோள்கள்[தொகு]
- ↑ "காப்பகப்படுத்தப்பட்ட நகல்" (PDF). Archived from the original (PDF) on 2014-05-14. பார்க்கப்பட்ட நாள் 2016-03-15.
- ↑ Definition of Oblong. Mathsisfun.com. Retrieved 2011-11-13.
- ↑ Oblong – Geometry – Math Dictionary. Icoachmath.com. Retrieved 2011-11-13.
- ↑ Harold Scott MacDonald Coxeter; Longuet-Higgins, M.S.; Miller, J.C.P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 246 (916): 401–450. doi:10.1098/rsta.1954.0003. பன்னாட்டுத் தர தொடர் எண்:0080-4614.
- ↑ Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition", Information Age Publishing, 2008, pp. 34–36 பன்னாட்டுத் தரப்புத்தக எண் 1-59311-695-0.
- ↑ Owen Byer; Felix Lazebnik; Deirdre L. Smeltzer (19 August 2010). Methods for Euclidean Geometry. MAA. பக். 53–. பன்னாட்டுத் தரப்புத்தக எண்:978-0-88385-763-2. http://books.google.com/books?id=W4acIu4qZvoC&pg=PA53. பார்த்த நாள்: 2011-11-13.
- ↑ 7.0 7.1 Martin Josefsson, "Five Proofs of an Area Characterization of Rectangles", Forum Geometricorum 13 (2013) 17–21.
- ↑ An Extended Classification of Quadrilaterals பரணிடப்பட்டது 2019-12-30 at the வந்தவழி இயந்திரம் (An excerpt from De Villiers, M. 1996. Some Adventures in Euclidean Geometry. University of Durban-Westville.)
- ↑ de Villiers, Michael, "Generalizing Van Aubel Using Duality", Mathematics Magazine 73 (4), Oct. 2000, pp. 303-307.
- ↑ Cyclic Quadrilateral Incentre-Rectangle பரணிடப்பட்டது 2011-09-28 at the வந்தவழி இயந்திரம் with interactive animation illustrating a rectangle that becomes a 'crossed rectangle', making a good case for regarding a 'crossed rectangle' as a type of rectangle.
- ↑ Hall, Leon M., and Robert P. Roe (1998). "An Unexpected Maximum in a Family of Rectangles". Mathematics Magazine 71 (4): 285–291. http://web.mst.edu/~lmhall/Personal/HallRoe/Hall_Roe.pdf.
- ↑ Lassak, M. (1993). "Approximation of convex bodies by rectangles". Geometriae Dedicata 47: 111. doi:10.1007/BF01263495.
- ↑ Stars: A Second Look பரணிடப்பட்டது 2016-03-03 at the வந்தவழி இயந்திரம். (PDF). Retrieved 2011-11-13.
வெளி இணைப்புகள்[தொகு]
- இயக்கமூட்டப்பட்ட விளக்கப் படம்
- Weisstein, Eric W., "Rectangle", MathWorld.
- Definition and properties of a rectangle with interactive animation.
- Area of a rectangle with interactive animation.











