சூழ்தொடு வட்டம்

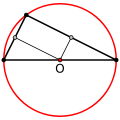
சூழ்தொடு வட்டம் என்பது முக்கோணம், கட்டம், ஐங்கோணம் போன்ற பல்கோண வடிவின் ஒவ்வொரு முனையையும் தொட்டுக்கொண்டு இருக்குமாறு வரையப்படும் வட்டம் ஆகும்.

சூழ்தொடு வட்டம் என்பது ஒரு பல்கோண வடிவின் ஒவ்வொரு முனையையும் தொட்டுக்கொண்டு இருக்குமாறு வரையப்படும் வட்டம் ஆகும். ஒரே நீளமும் கோணமும் கொண்ட பக்கங்களைக் கொண்ட சீரான பல்கோணங்கள் எல்லாவற்றுக்கும் சூழ்தொடு வட்டம் வரைய இயலும். ஆனால் பக்க நீளங்கள் ஒரே அளவாக இல்லாத பல்கோணங்கள் யாவற்றுக்கும் சூழ்தொடு வட்டம் வரைய இயலாது எனினும், சிலவற்றுக்கும் சூழ்தொடு வட்டம் வரைய இயலும். கீழ்க்காணும் படத்தில் ஒரு எடுத்துக் காட்டைப் பார்க்கலாம்.

பக்க நீளங்கள் வேறுபடும் ஒரு பல்கோணத்தைச் சுற்றி இருக்கும் சூழ்தொடு வட்டம்

மேலும் பார்க்க

• உள்தொடு வட்டம்
• உள்தொடு உருண்டை
• சூழ்தொடு உருண்டை