சைன்
 | |
| அடிப்படைக் கூறுகள் | |
| சமநிலை | ஒற்றை |
| ஆட்களம் | (-∞,∞) |
| இணையாட்களம் | [-1,1] |
| காலமுறைமை அளவு | 2π |
| குறிப்பிட்ட அளவுகள் | |
| பூச்சியத்தில் | 0 |
| பெரும மதிப்பு | ((2k+½)π,1) |
| சிறும மதிப்பு | ((2k-½)π,-1) |
| குறிப்பிட்ட கூறுகள் | |
| சார்பின் மூலம் | kπ |
| மாறுநிலைப் புள்ளி | kπ-π/2 |
| வளைவுமாற்றுப் புள்ளி | kπ |
| மாறாப்புள்ளி | 0 |
| மாறி k ஒரு முழு எண் | |
கணிதத்தில் செவ்வளைவு அல்லது சைன் (Sine) சார்பு என்பது ஒரு கோணத்தின் சார்பாகும். கோணங்களின் சார்புகளாக அமையும் ஆறு முக்கோணவியல் சார்புகளில் இது முதல் சார்பாக வரிசைப்படுத்தப்படுகிறது. ஒரு செங்கோண முக்கோணத்தில், ஒரு கோணத்தின் சைன் சார்பு, அக்கோணத்தின் எதிர்ப்பக்கத்திற்கும் செம்பக்கத்திற்குமுள்ள விகிதமாகும். ஓரலகு வட்டம், சாய்வு, முடிவிலாத்தொடர் முதலியவை வாயிலாகவும் மற்றும் வகைக்கெழுச் சமன்பாடுகளின் தீர்வாகவும் சைன் சார்பை வரையறுக்கலாம்.
ஒலி, ஒளி அலைகளின் காலமுறைமை, சீரிசை அலையியற்றியின் நிலை மற்றும் திசைவேகம், சூரிய ஒளியின் செறிவு, பகல் பொழுதின் நீளம் மற்றும் ஒரு ஆண்டு முழுவதற்குமான சராசரி வெப்ப அளவு போன்ற கருத்துகளை விளக்க, சைன் சார்பு பயன்படுகிறது.
சமஸ்கிருதத்திலிருந்து அரபு மொழிக்கும் அரபு மொழியிலிருந்து இலத்தீன் மொழிக்கும் இடம் பெயர்ந்த, குப்தர்கள் காலத்து இந்திய வானவியலில் (ஆர்யபட்டியம், சூரிய சித்தாந்தம்) பயன்படுத்தப்பட்ட ஜியா மற்றும் கோட்டி-ஜியா சார்புகள் சைன் சார்பின் மூலங்களாகும்.[1] பாதி நாண் எனும் பொருள் கொண்ட ஜிய- ஆர்த என்ற சமஸ்கிருதச் சொல் அரபு மொழியில் ஜிபா (jiba) என மொழிபெயர்க்கப்பட்டுப் பின் ஜிப் (jb) என சுருக்கமடைந்து பின், ஜெய்ப் (jaib) என திரிந்து, விரிகுடா என்ற பொருளுடைய சைனஸ் (sinus) எனும் வார்த்தையாக இலத்தீன் மொழியில் மொழிபெயர்க்கப்பட்டுள்ளது. இந்த சைனஸ் வார்த்தையிலிருந்து சைன் என்ற பெயர் ஏற்பட்டது.[2],
செங்கோண முக்கோணத்தில் வரையறை[தொகு]

வடிவொத்த முக்கோணங்களின் ஒத்தபக்கங்களின் விகிதங்கள் சமமாக இருக்கும் என்ற உண்மையிலிருந்து, ஒரு முக்கோணத்தின் பக்க நீளங்களுக்கும் கோண அளவுகளுக்கும் தொடர்பு இருக்கும் என்ற கருத்து அறியப்படுகிறது. இரு செங்கோண முக்கோணங்களில் ஒன்றின் செம்பக்கம் மற்றதன் செம்பக்க நீளத்தைப் போல இருமடங்கு எனில் மற்ற பக்கங்களும் அவ்வாறே அமையும். இந்த பக்க விகிதங்களைத்தான் முக்கோணவியல் சார்புகள் தருகின்றன.
ஒரு செங்கோண முக்கோணத்தின் கோணம் A -ன் முக்கோணவியல் சார்புகளை வரையறுக்க அம்முக்கோணத்தின் பக்கங்களைப் பின்வருமாறு அழைக்கலாம்:
- செம்பக்கம் (அல்லது கர்ணம்) (hypotenuse):
செங்கோணத்திற்கு எதிர்ப்பக்கம். இதன் அளவு h. ஒரு செங்கோண முக்கோணத்தில் செம்பக்கந்தான் மூன்று பக்கங்களிலும் நீளமானது.
- எதிர்ப்பக்கம் (opposite):
நாம் எடுத்துக்கொண்ட கோணம் A -க்கு எதிரில் அமையும் பக்கம். இதன் நீளம் a.
- அடுத்துள்ள பக்கம் (adjacent):
செங்கோணம் மற்றும் நாம் எடுத்துக்கொண்ட கோணம் இரண்டிற்கும் ( A மற்றும் C) பொதுவான பக்கம். இதன் நீளம் b.
சைன் சார்பு:
செங்கோண முக்கோணத்தின் ஒரு கோணத்தின் சைன் மதிப்பு, அக்கோணத்தின் எதிர்ப்பக்கம் மற்றும் செம்பக்கத்தின் விகிதமாகும்.
A கோணத்தைக் கொண்ட அனைத்து செங்கோண முக்கோணங்களிலும் இவ்விகிதத்தின் மதிப்பு ஒரே மதிப்புடையதாய் அமையும். அச்செங்கோண முக்கோணங்கள் எல்லாம் வடிவொத்த முக்கோணங்கள் என்பதால் அவற்றின் பக்க அளவுகள் வெவ்வேறாக இருந்தாலும் அவற்றின் அவ்வேறுபாடு இவ்விகிதத்தின் மதிப்பைப் பாதிப்பதில்லை.
வரையறை- சாய்வு வாயிலாக[தொகு]
செங்கோண முக்கோணங்களின் மூலம் வரையறுப்பது போல ஒரு கிடைமட்டக்கோட்டுடன் தொடர்புடைய ஒரு கோட்டுத்துண்டின் எழுச்சி (rise), ஓட்டம்(run), சாய்வு ஆகியவற்றின் மூலமாகவும் முக்கோணவியல் சார்புகளை வரையறுக்கலாம்.
எடுத்துக்கொள்ளப்பட்ட கோட்டுத்துண்டின் நீளம் 1 அலகு என்க. அக்கோட்டுத்துண்டு ஒரு குறிப்பிட்ட கிடைமட்டக்கோட்டுடன் உருவாக்கும் கோணம் A என்க. இக்கோணத்தின்:
- சைன் மதிப்பு, கோட்டுத்துண்டின் செங்குத்தான எழுச்சியின் அளவுக்குச் சமம்.
- SinA = எழுச்சி
கோட்டுத்துண்டின் நீளம் சாய்வின் மதிப்பை பாதிப்பதில்லை. ஆனால் எழுச்சி மற்றும் ஓட்டத்தின் மதிப்புகள் கோட்டுத்துண்டின் நீளத்தைச் சார்ந்துள்ளன. கோட்டுத்துண்டின் நீளம் 1 அலகாக இல்லையென்றால் குறிப்பிட கோணத்தில் அக்கோட்டுத்துண்டின்
- எழுச்சியைக் காண அக்கோணத்தின் சைன் மதிப்பை கோட்டுத்துண்டின் நீளத்தால் பெருக்கிக் கொள்ள வேண்டும்.
எடுத்துக்காட்டாக:
கோட்டுத்துண்டின் நீளம் 5 அலகுகள் எனில் 7° கோணத்தில் அக்கோட்டுத்துண்டின்:
எழுச்சி = 5 sin(7°)
வரையறை- ஓரலகு வட்டம் வாயிலாக[தொகு]
ஆறு முக்கோணவியல் சார்புகளையும் ஓரலகு வட்டத்தைக் கொண்டு வரையறுக்கலாம். ஓரலகு வட்டம் என்பது ஆதிப்புள்ளியை மையமாகவும் ஆரம் 1 அலகும் கொண்ட வட்டமாகும். நடைமுறைக் கணக்கீடுகளுக்கு ஓரலகு வட்டத்தின் மூலமான வரையறை அவ்வளவாகப் பொருந்தாவிடினும், (0, π/2 ) -ல் அமையும் கோணங்களுக்கு மற்றுமல்லாது அனைத்து மெய்யளவு கோணங்களுக்கும் பொருத்தமாக அமையும்.
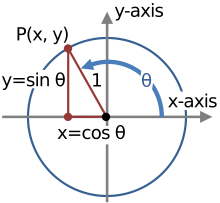
x-அச்சின் நேர்மப் பகுதியோடு, ஆதிப்புள்ளியில் θ கோணம் உண்டாக்கும் ஒரு கோடு ஓரலகு வட்டத்தை சந்திக்கிறது என்க. அந்த சந்திக்கும் புள்ளியின் x- மற்றும் y-அச்சுதூரங்கள் முறையே cos θ மற்றும் sin θ -க்குச் சமம். செங்கோண முக்கோண முறை வரையறைப்படியும் இதை உணரலாம். வெட்டும் புள்ளியின் அச்சுதூரங்கள்: (x, y) என்க. ஓரலகு வட்டத்தின் ஆரம் செங்கோண முக்கோணத்தின் செம்பக்கம். எனவே செம்பக்கத்தின் அளவு 1 அலகு.
 |
 |
 |

முடிவிலாத் தொடரின் வாயிலாக[தொகு]

டெயிலரின் விரிவுக் கோட்பாட்டைப் பயன்படுத்திப் பின்வரும் முற்றொருமையை, எல்லா மெய்யெண்கள் x -க்கும் உண்மையெனக் காட்டலாம்.[3]
வகைக்கெழுச் சமன்பாட்டின் வாயிலாக[தொகு]
சைன் சார்பு பின்வரும் வகைக்கெழுச் சமன்பாட்டை நிறைவு செய்யும் தீர்வாக அமையும்:
- என்ற ஆரம்ப நிபந்தனையை நிறைவு செய்யும் தனித்த தீர்வு சைன் சார்பாகும்.
முற்றொருமைகள்[தொகு]
-ன் அனைத்து மதிப்புகளுக்கும் பின்வரும் முற்றொருமைகள் மெய்யாகும்:
- =
- =
- =
- =
- =
தலைகீழி[தொகு]
சைன் சார்பின் தலைகீழிச் சார்பு கோசீக்கெண்ட் சார்பு.
sin(A) -ன் தலைகீழி csc(A), அல்லது cosec(A):
நேர்மாறு[தொகு]

சைன் சார்பின் நேர்மாறுச் சார்பு arcsine (arcsin) அல்லது(sin−1).
k ஏதாவதொரு முழு எண்:
மேலும்:
காற்பகுதிகள் தொடர்பான பண்புகள்[தொகு]
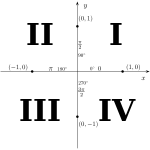
நான்கு காற்பகுதிகளிலும் சைன் சார்பு அமையும் விதத்தைப் பின்வரும் அட்டவணை தருகிறது.
| காற்பகுதி | பாகை | ரேடியன் | மதிப்பு | குறி | ஓரியல்புத் தன்மை | குவிவுத்தன்மை |
|---|---|---|---|---|---|---|
| முதல் காற்பகுதி | கூடும் சார்பு | குழிவு | ||||
| இரண்டாம் காற்பகுதி | குறையும் சார்பு | குழிவு | ||||
| மூன்றாம் காற்பகுதி | குறையும் சார்பு | குவிவு | ||||
| நான்காம் காற்பகுதி | கூடும் சார்பு | குவிவு |
காற்பகுதிகளுக்கு இடைப்பட்ட புள்ளிகளில், k ஒரு முழு எண்.

| பாகை | ரேடியன்
0 ≤ x < 2π |
ரேடியன் | sin x | புள்ளி வகை |
|---|---|---|---|---|
| 0 | 0 | sin x = 0, சமன்பாட்டின் மூலம், வளைவுமாற்றுப் புள்ளி | ||
| 1 | பெரும மதிப்பு | |||
| 0 | sin x = 0, சமன்பாட்டின் மூலம், வளைவுமாற்றுப் புள்ளி | |||
| -1 | சிறும மதிப்பு |
அட்டவணையில் இல்லாத கோணங்களுக்கு, சைன் சார்பு 360° (2π rad) அளவு கால முறைமை கொண்டது என்ற கூற்றினைப் பயன்படுத்தி காணலாம்:
,
அல்லது
-ஐப் பயன்படுத்தலாம்.
மேலும்
நுண்கணிதம்[தொகு]
சைன் சார்பு:
நுண்கணிதத்தில் இச்சார்பின்:
C, தொகையீட்டு மாறிலி.
மேற்கோள்கள்[தொகு]
- ↑ Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc.. பன்னாட்டுத் தரப்புத்தக எண் 0-471-54397-7, p. 210.
- ↑ Oxford English Dictionary, sine, n.2
- ↑ See Ahlfors, pages 43–44.
















































