கோணம்


ஒரே புள்ளியில் இருந்து கிளம்பும் இரண்டு கதிர்கள் உருவாக்கும் வடிவம் கோணம் (Angle) எனப்படுகிறது[1]. வெட்டிக்கொள்ளும் இரண்டு கோடுகளின் சாய்வுகளின் வித்தியாசம் காண கோணம் உதவுகிறது. கோணங்களை அளக்கும் அலகுகளுள் பாகை ஒரு வகையாகும். இதன் குறியீடு °.
ஒரு தளத்திலமைந்த இரு கதிர்களால் கோணம் உருவாகிறது. இத்தளம் யூக்ளிடிய தளமாக இருக்க வேண்டிய அவசியமில்லை. யூக்ளிடிய வெளியிலும், பிற வெளிகளிலும் இரு தளங்கள் வெட்டிக் கொள்வதால் கோணங்கள் உருவாகின்றன. இக்கோணங்கள் இருமுகக் கோணங்கள் (dihedral angles) எனப்படுகின்றன. தளத்திலமைந்த இரு வளைகோடுகளுக்கு இடையே உருவாகும் கோணம், அவை வெட்டிக்கொள்ளும் புள்ளிகளில் அவ்வளைகோடுகளுக்கு வரையப்படும் தொடுகோடுகளுக்கு இடைப்பட்ட கோணமாகும். இதேபோல, ஒரு கோளத்தின் இரு பெரு வட்டங்களுக்கு இடையே உருவாகும் கோளக் கோணமானது அவ்விரு பெருவட்டங்களால் தீர்மானமாகும் தளங்களுக்கு இடைப்பட்ட இருமுகக் கோணம் ஆகும்.
கோணங்களின் குறியீடுகள்
[தொகு]பொதுவாக கோணங்களின் அளவைக் குறிக்கும் மாறிகளைக் குறிப்பதற்கு கிரேக்க எழுத்துக்கள் (α, β, γ, θ, φ, ...) பயன்படுத்தப்படுகின்றன. ஆங்கில எழுத்துக்களாலும் கோணங்கள் குறிக்கப்படுகின்றன.
வடிவவியல் வடிவங்களில் கோணங்களை வரையறுக்கும் மூன்று புள்ளிகளோடு இணைக்கப்படும் குறியீடுகளாலும் அறியப்படுகின்றன. எடுத்துக்காட்டாக, AB , AC கதிர்களால் உருவாகும் கோணத்தின் குறியீடு: ∠BAC அல்லது சில சமயங்களில், கோணத்தின் முனையை மட்டும் குறிப்பிடும் ஒற்றை எழுத்தால் மட்டும் (∠A) குறிக்கப்படுகிறது.
கோண வகைகள்
[தொகு]தனிப்பட்ட கோணங்கள்
[தொகு]செங்கோணம், குறுங்கோணம், விரிகோணம், நேர்கோணம், சாய்வுக் கோணம், பின்வளைகோணம் ஆகியன சில கோணவகைகளாகும்.
பூஜ்ஜிய கோணம்
[தொகு]ஒரே புள்ளியில் ஆரம்பிக்கும் இரு கதிர்களுக்கு இடைப்பட்ட தூரம் 0 பாகை எனில் அக்கோணம் பூஜ்ஜிய கோணம் எனப்படும்.
செங்கோணம்
[தொகு]
90 பாகை அளவுள்ள கோணம், செங்கோணம் எனக் குறிப்பிடப்படுகின்றது. இரு நேர்கோடுகள் ஒன்றோடு ஒன்று முட்டும்போது அவற்றுக்கு இடைப்பட்ட கோணம் சரியாக 90 பாகையாக இருந்தால் அது செங்கோணம் எனப்படும்.
குறுங்கோணம்
[தொகு]
இரு நேர்கோடுகள் ஒன்றோடு ஒன்று முட்டும்போது 90 பாகைக்கும் குறைவாக இருந்தால் அது குறுங்கோணம் ஆகும்.
எடுத்துக்காட்டு : 15°, 30°,60°,75° கோணங்கள்
விரிகோணம்
[தொகு]
இரு நேர்கோடுகள் ஒன்றோடு ஒன்று முட்டும்போது 90 பாகைக்கு அதிகமாகவும் 180 பாகைக்கும் குறைவாக இருந்தால் அது விரிகோணம் ஆகும்.
x° = விரிகோணம் எனில்:
- 90° <x° < 180° ஆக அமையும்.
நேர் கோணம்
[தொகு]
இரு நேர்கோடுகள் ஒன்றோடு ஒன்று முட்டும்போது சரியாக 180 பாகையாக இருந்தால் அது நேர் கோணம். ஒரு கோணத்தின் கதிர்கள் , எதிர்க்கதிர்களாக உருவாகும்போது நேர்கோடு உருவாகிறது .
பின்வளை கோணம்
[தொகு]180° க்கும் 360° க்கும் இடைப்பட்ட அளவுகளைக் கொண்ட கோணம் பின்வளை கோணம் (reflex angles) அல்லது மடக்கு கோணம் ஆகும்.
முழுக் கோணம்
[தொகு]
360° அல்லது 2π ரேடியன் அளவுள்ள கோணம் முழுக் கோணம்.
சாய்வுக் கோணம்
[தொகு]90° ஆகவும் 90° இன் மடங்காகவும் இல்லாத கோணங்கள் சாய்வுக் கோணங்கள்.
நிரப்புக்கோணங்கள்
[தொகு]இரண்டுகோணங்களின் கூடுதல் 90 என்றால் அந்த இரண்டு கோணங்களும் நிரப்புக்கோணங்கள் ஆகும் . ஒவ்வொரு கோணமும் மற்றோரு கோணத்தின் நிரப்பு கோணம் ஆகும் .
30° இன் நிரப்புக்கோணம் 60° ஆகும் . மற்றும் 60° இன் நிரப்புக்கோணம் 30°
மிகை நிரப்புக்கோணம்
[தொகு]இரண்டுகோணங்களின் கூடுதல் 180 என்றால் அந்த இரண்டு கோணங்களும் நிரப்புக்கோணங்களும் மிகை நிரப்புக்கோணம் ஆகும் . ஒவ்வொரு கோணமும் மற்றோரு கோணத்தின் மிகை நிரப்பு கோணம் ஆகும் .
120° இன் மிகை நிரப்பு கோணம் 60°, 60° இன் மிகை நிரப்பு கோணம் 120
அட்டவணை
[தொகு]கோணங்களின் பெயர்கள், இடைவெளிகள், அலகுகள் கீழே அட்டவணப்படுத்தப் பட்டுள்ளன:
| பெயர் | குறுங்கோணம் | செங்கோணம் | விரிகோணம் | நேர்கோணம் | பின்வளைகோணம் | முழுக்கோணம் | ||||
| Units | இடைவெளி | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| சுற்றுகள் | ||||||||||
| ரேடியன்கள் | ||||||||||
| பாகைகள் | (0,90)° | 90° | (90,180)° | 180° | (180,360)° | 360° | ||||
சமான கோணச் சோடிகள்
[தொகு]- சமவளவுள்ள கோணங்கள், சம கோணங்கள் அல்லது சர்வசமக் கோணங்கள்.
- சுற்றின் முழுஎண் மடங்கான சுற்றுகளில் அளவில் வேறுபாடு கொண்டவையாகவும், ஒரே கதிரை தங்களது முடிவுப் பக்கங்களாகவும் கொண்ட இரு கோணங்கள் ஒருமுடிவுக் கோணங்கள் (coterminal angles).
- ஒரு கோணத்தின் குறுங்கோண வடிவம் அதன் குறிப்பீட்டுக் கோணம்.
- எடுத்துக்கொள்ளப்பட்ட ஒரு கோணத்தின் அளவிலிருந்து தேவைக்கேற்பத் தொடர்ந்து நேர்கோண மதிப்பைக் (1/2 சுற்று, 180°, π ரேடியன்) கூட்டுவது அல்லது கழிப்பதன் மூலம் பெறப்படும் குறுங்கோண வடிவமானது (0 - 1/4 சுற்று, 90°, அல்லது π/2 ரேடியன்), அதன் குறிப்பீட்டுக் கோணம்[2].
- எடுத்துக்காட்டாக,
- 30° இன் குறிப்பீட்டுக் கோணம் 30°
- 150° இன் குறிப்பீட்டுக் கோணம் 30° (180°-150° = 30°)
- 750° இன் குறிப்பீட்டுக் கோணம் 30° (750 - 4x180°) = 30°)
- 45° இன் குறிப்பீட்டுக் கோணம் 45°
- 225° இன் குறிப்பீட்டுக் கோணம் 45° (225°-180°=45°)
- 405° இன் குறிப்பீட்டுக் கோணம் 45° (405°-2x180=45°)
எதிர் கோணங்களும் அடுத்துள்ள கோணங்களும்
[தொகு]
இரு கோடுகள் ஒரு புள்ளியில் வெட்டிக்கொள்ளும்போது நான்கு கோணங்கள் உருவாகின்றன. இவை ஒன்றுக்கொன்று அமைந்திருக்கும் விதத்தைக் கொண்டு எதிர் கோணங்கள், அடுத்துள்ள கோணங்கள் எனச் சோடிகளாகப் பிரிக்கப்பட்டு அழைக்கப்படுகின்றன.
- எதிர் கோணங்கள்
ஒன்றுக்கொன்று எதிராக அமையும் ("X"-வடிவிலமையும்) கோணச் சோடிகள், குத்துநிலை கோணங்கள், எதிர் கோணங்கள், குத்தெதிர் கோணங்கள் என அழைக்கப்படுகின்றன.[3]
- ஒரு சோடி எதிர் கோணங்கள் சமமானவை. இக்கூற்று குத்துக்கோணத் தேற்றம் ஆகும். இத்தேற்றம் தேலேசால் நிறுவப்பட்டது.[4][5] இருசோடி எதிர் கோணங்களும் அடுத்துள்ள கோணங்களுக்கு மிகைநிரப்பிகளாக அமைவதால் எதிர் கோணங்கள் சமவளவானவை எனக் காட்டப்பட்டுள்ளது.
ஒரு வரலாற்றுக் குறிப்பின்படி[5], தேலேசு எகிப்திற்குச் சென்றபோது, இரு வெட்டிக்கொள்ளும் கோடுகளை வரைந்தபோதெல்லாம் அவற்றின் எதிர் கோணங்களை அளந்து அவை சமமாய் இருப்பதை எகிப்தியர்கள் உறுதி செய்துகொண்டதைக் கண்டார். அதனால், நேர்க்கோணங்கள் எல்லாம் சமமானவை என்பதாலும், சமமானவற்றோடு சமமானவற்றைக் கூட்டுவதலோ கழிப்பதலோ கிடைக்கக்கூடியவையும் சமமானவையாகவே இருக்கும் என்ற பொதுக் கருத்தின்படியும், அனைத்து எதிர் கோணங்களும் சமம் எனத் தேலேசு நிறுவினார் என அறியப்படுகிறது.
மேலுள்ள படத்தில் கோணம் A = x எனக் கொள்ளலாம். இரு அடுத்துள்ள கோணங்கள் ஒரு நேர்கோட்டை அமைப்பதால் அவை மிகைநிரப்பு கோணங்கள். கோணங்கள் A , C இரண்டும் அடுத்துள்ள கோணங்களாக இருப்பதால்,
- C = 180 − A = 180 − x.
இதேபோல A , D இரண்டும் அடுத்துள்ள கோணங்கள் என்பதால்.
- D = 180 − A = 180 − x.
- எனவே எதிர் கோணங்கள் C , D இரண்டும் சர்வசமம்.
இதேமுறையில் எதிர் கோணங்கள் A , B இரண்டும் சர்வசமம் என நிறுவலாம்
- அடுத்துள்ள கோணங்கள்
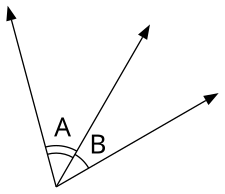
ஒரே உச்சியையும் ஒரு பொதுப் பக்கத்தையும் கொண்ட கோணங்கள் அடுத்துள்ள கோணங்கள் ஆகும். அடுத்துள்ள கோணங்களுக்கு வேறு உட்புள்ளிகள் எதுவும் பொதுவாக இருக்காது. அதாவது அடுத்துள்ள கோணங்கள் அடுத்தடுத்து ஒரு பொதுக்கரத்துடன் இருக்கும்.
- இரு அடுத்துள்ள கோணங்களின் கூடுதல் 90° எனில் அவை நிரப்பு கோணங்கள்;
- இரு அடுத்துள்ள கோணங்களின் கூடுதல் 180° எனில் அவை மிகைநிரப்புக் கோணங்கள்
இரு கோடுகளை (பொதுவாக இணை கோடுகள் ஒரு குறுக்கு வெட்டி வெட்டும்போது, உருவாகும் கோணங்கள் உட்கோணங்கள், வெளிக்கோணங்கள், ஒத்த கோணங்கள், ஒன்றுவிட்ட உட்கோணங்கள் என வகைப்படுத்தப்படுகின்றன.[6]
கோணங்களை அளத்தல்
[தொகு]பொதுவாக ஒரு கோணத்தின் அளவு, அக்கோணத்தின் ஒரு கரத்தை மற்றொன்றுடன் பொருந்தச் செய்யத் தேவையான சுழற்சியின் அளவாகக் கொள்ளப்படுகிறது. சமவளவு கொண்ட கோணங்கள் சமகோணங்கள், சர்வசம கோணங்கள் அல்லது சமவளவுள்ள கோணங்கள் என அழைக்கப்படுகின்றன. கோணங்களின் முக்கிய அலகுகள் பாகைகள், ரேடியன்கள், சுற்று இன்னும் சில ஆகும்.
கோணத்தின் அலகுகள்
[தொகு]1. பாகை பாகை என்பது கோணத்தை அளப்பதற்குரிய ஒரு அலகு ஆகும். இது 60 கலைக்குச் சமனானது ஆகும். இது ° என்னும் குறியீட்டினால் குறிக்கப்படுவது வழக்கம். 60° என எழுதும்போது அது 60 பாகை என்பதைக் குறிக்கும். ஒரு தளத்தில் அதிலுள்ள ஒரு புள்ளியை முழுவதுமாகக் சுற்றி அமையும் கோணம் 360 பாகை (360°) ஆகும். பொதுவான தேவைகளுக்கு ஒரு பாகை என்பது போதுமான அளவு சிறிய அலகு ஆகும். ஆனால் வானியல் போன்ற தொலை தூர நிகழ்வுகளைக் கையாளும் துறைகளில் ஒரு பாகை என்பது ஒப்பீட்டளவில் சிறியது அல்ல.
2.ரேடியன் ஆரையம் என்பது ஒரு கோண அளவு. இதனை ரேடியன் என்றும் கூறுவர். ஒரு வட்டத்தின் வளைவு வெட்டின் (வில்லின்) நீளம் அவ் வட்டத்தின் ஆரத்திற்கு (ஆரைக்கு) சமம் என்றால் அவ் வளைவு வெட்டானது (வில்லானது) வட்டத்தின் நடுவே வடிக்கும் கோணம் ஓர் ஆரையம் ஆகும். வட்டத்தின் ஒரு சுற்றின் மொத்தக் கோணத்தின் அளவு இந்த 2π ஆரையம் (ரேடியன்) (கிட்டத்தட்ட 6.28318531 ஆரையம்). ஆரையத்தின் ஆங்கிலச் சொல்லாகிய ரேடியன் என்னும் அலகை rad எனக் குறிப்பர். தமிழில் ஆரையம் அல்லது ரேடி எனக் குறிக்கப்படும். பாகைக் கணக்கில் ஓர் ஆரையம் என்பது 180π அல்லது 57.2958 பாகை ஆகும
1.கோணமானி (Angle Dekker)
'கோணமானியானது தானிணை ஒளிமானியின் அடிப்படையில் செய்யப்பட்டது ஆகும். இதில், இணை ஆடியின் குவிமையத்தில், ஒரு குறுக்குக் கம்பிக்கு பதிலாக, ஒரு அளவுகோல் பதியப்பட்டிருக்கும். இது ஒளிக் கதிரோடு சென்று எதிரொளிக்கும் பரப்பின் மேல் பட்டு, விழியாடியின் பார்வை தளத்தில் வைக்கப்பட்டுள்ள இன்னொரு அளவு கோலின் மேல் செங்குத்தாக விழும். இந்த இரண்டு அளவு கோல்களும் எவ்வாறு இணைகின்றன என்பதைப் பொறுத்து, கோணத்தை அளக்கபயன்படுகிறது'.
2. சரிவு கோண அளவிகள் (Bevel Protractors)
கோணத்தை வரைவதற்கும், அளப்பதற்கும் அரைவட்ட அல்லது முழுவட்ட கோண அளவிகளைப் பயன்படுத்துவோம் . ஒரு முழு வட்ட கோண அளவியின் மையத்தில் சுற்றும் வகையில் ஒரு வட்டத் தட்டைப் பொருத்தி, அதில் ஒரு வெர்னியர் அளவுகோலை அமைத்துவிட்டால், இந்த வட்டத்தட்டு, எவ்வளவு கோணத்துக்கு சுற்றுகிறது என்பதைத் துல்லியமாகக் கணக்கிட்டுவிடலாம்.சரிவு கோணஅளவியின் அடிப்பாகத்தில் ஒரு சட்டத்தை நிலையாகப் பொருத்திவிட்டு, சுற்றும் வட்டத் தட்டில் ஒரு நீண்ட சட்டத்தை பொருத்திவிட்டால், இச்சட்டம் சுற்றும் போது அதற்கும் அடிச்சட்டத்துக்கும் இடையில் உள்ள கோணத்தை எளிதாக அளந்து விடலாம். இதன் அடிப்படையில் அமைக்கப்பட்டதே சரிவு கோண அளவிகள் ஆகும்.
3. சாய்வுமானி (Clino meter)
சாய்வாக இருக்கும் கோணத்தை துல்லியமாக அளக்க கோணஅளவியோ, சாராய மட்டமோ பயன்படாது. ஏனென்றால் கோணஅளவிக்கு கோணத்தை அளக்கும் இரண்டு பரப்புகள் தேவை. சாராய மட்டமோ குறைவான கோணத்தையே அளக்கவல்லது. இக்குறையை போக்க கோணமானியையும், சாராய மட்டத்தையும் இணைத்து ஒரு புதிய கருவி உருவாக்கப்பட்டது. இதற்கு பெயர் தான் சாய்வுமானி ஆகும்.
4. கோண கடிகைகள் (Angle gauges)
கோண அளவுக்கு ஏற்ப நிலையாக இருப்பது தான் கோண கடிகைகள் ஆகும்.இவை செவ்வக வடிவத்தில், பல கோண அளவுகளில் செய்யப்பட்ட கலப்பு எஃகினால் ஆனது ஆகும். இதன் அளக்கும் பரப்பு வழவழப்பாக, ஒன்றன் மேல் ஒன்றை வைத்து நகர்த்தினால், பற்றிக் கொள்ளும் வகையில் இருக்கும்.
நேர்கோணமும், எதிர்கோணமும்
[தொகு]கோணத்தின் வரையறையில் எதிர்கோணக் கருத்துரு இல்லையென்றாலும், திசைப்போக்கு, எதிர் திசை சுழற்சியைக் குறிப்பதற்கு நேர், எதிர் கோண கருத்துரு உதவியாய் அமையும்.
இருபரிமாண கார்ட்டீசிய ஆள்கூற்று முறைமையில், ஆதிப்புள்ளியை உச்சியாகவும், நேர் x-அச்சைத் தொடக்கப் பக்கமாவும் கொண்டு கோணம் வரையறுக்கப்படுகிறது. தொடக்கப் பக்கத்திலிருந்து பாகை, ரேடியன் அல்லது சுற்றில் அளக்கப்படும் கோண அளவைக் கொண்டு முடிவுப்பக்கம் அமைகிறது. நேர் x-அச்சிலிருந்து நேர் y-அச்சை நோக்கி நிகழும் சுழற்சி நேர் கோணங்கள்; நேர் x-அச்சிலிருந்து எதிர் y-அச்சை நோக்கி நிகழும் சுழற்சி எதிர் கோணங்கள்; கார்டிசியன் ஆள்கூறுகளின் திட்ட வடிவில் (x-அச்சு வலப்புறமும் y-அச்சு மேற்புறமாகவும் அமைதல்) நேர் சுழற்சியானது எதிர்க் கடிகாரத்திசையாகவும், எதிர் சுழற்சியானது கடிகாரத்திசையாகவும் இருக்கும்.
பல இடங்களில் −θ கோணம் என்பது, ஒரு முழுச் சுற்றுக் கோணத்திலிருந்து θ கோணவளவைக் கழித்தபின் கிடைக்கும் கோணத்திற்குச் சமானமானது. எடுத்துக்காட்டாக, −45° என்பது or 315° க்குச் (360° − 45°) சமானம். எனினும் −45° சுழற்சியும் 315° சுழற்சியும் ஒன்றாகாது.
முப்பரிமாணத்தில் கடிகாரத் திசை, எதிர் கடிகாரத் திசை என்பதற்குப் பொருளில்லை. எனவே நேர் கோணம், எதிர் கோணங்களின் திசையை வரையறுப்பதற்கு, கோணத்தின் உச்சிவழியாக, கோணத்தின் பக்கங்கள் அமையும் தளத்திற்குச் செங்குத்தான திசையன் ஆதாரமாக எடுத்துக் கொள்ளப்படுகிறது.
மேற்கோள்கள்
[தொகு]- ↑ Sidorov, L.A. (2001), "Angle", in Hazewinkel, Michiel (ed.), Encyclopedia of Mathematics, Springer, பன்னாட்டுத் தரப்புத்தக எண் 978-1556080104
- ↑ http://www.mathwords.com/r/reference_angle.htm
- ↑ Wong, TW; Wong, MS. "Angles in Intersecting and Parallel Lines". New Century Mathematics. Vol. 1B (1 ed.). Hong Kong: Oxford University Press. pp. 161–163. பன்னாட்டுத் தரப்புத்தக எண் 978-0-19-800176-8.
- ↑ Euclid (c. 300 BC). The Elements.
{{cite book}}: Check date values in:|year=(help) Proposition I:13. - ↑ 5.0 5.1 William G. Shute, William W. Shirk, George F. Porter, Plane and Solid Geometry, American Book Company (1960) pp. 25-27
- ↑ Jacobs, Harold R. (1974), Geometry, W.H. Freeman, p. 255, பன்னாட்டுத் தரப்புத்தக எண் 0-7167-0456-0
- ↑ "பாடம் : 1 அளவையியலின் தோற்றமும் வளர்ச்சியும்". பார்க்கப்பட்ட நாள் 12 சூன் 2017.
சுட்டிகள்
[தொகு]- கோணம் மற்றும் பிற அலகுகள் மாற்றப் பொறி பரணிடப்பட்டது 2005-05-07 at the வந்தவழி இயந்திரம்













