தேலேசுத் தேற்றம்

வடிவவியலில் தேலேசு தேற்றத்தின்(Thales' theorem) அல்லது தேல்சு தேற்றத்தின்(தமிழகப் பலுக்கல்) கூற்று: ஒரு வட்டத்தின் மீது அமையும் மூன்றும் புள்ளிகள் A, B மற்றும் C. மேலும் கோடு AC, வட்டத்தின் விட்டம் எனில், கோணம் ABC செங்கோணமாக அமையும். இத்தேற்றம் கிரேக்க கணிதவியலாளர் தேலேசு பெயரால் அழைக்கப்படுகிறது. பொதுவாக இத்தேற்றம் தேலேசுக்குரியதாகக் கருதப்பட்டாலும் சில சமயங்களில் இது கணிதவியலாளர் பித்தாகரசுக்குரியதாகவும் கருதப்படுகிறது.

நிறுவல்[தொகு]

இத்தேற்றத்தின் நிறுவலுக்குப் பின்வரும் மெய்க்கூற்றுகள் அல்லது அடிக்கோள்கள் பயன்படுத்தப்படுகின்றன:

ஒரு முக்கோணத்தின் மூன்று கோணங்களின் கூட்டல் 180°.
ஒரு இருசமபக்க முக்கோணத்தின் அடிக்கோணங்கள் சமம்.

நிறுவல்

வட்ட மையம் O .
OA = OB = OC, என்பதால் $\triangle OBA$ , $\triangle OBC$ இரண்டும் இருசமபக்க முக்கோணங்கள்.

எனவே அவற்றின் அடிக்கோணங்கள்:

$\angle OBC$ = $\angle OCB$

$\angle BAO$ = $\angle ABO$

α = $\angle BAO$ , β = $\angle OBC$ என்க.

$\triangle ABC$ -இன் மூன்று உட்கோணங்கள்:

α, α + β மற்றும் β.

\alpha +\left(\alpha +\beta \right)+\beta =180^{\circ }

{2}\alpha +{2}\beta =180^{\circ }

\alpha +\beta =90^{\circ }

அதாவது $\angle ABC$ = $90^{\circ }$

மறுதலை[தொகு]

தேலேசுத் தேற்றத்தின் மறுதலை உண்மையாகும். மறுதலைத் தேற்றத்தின் கூற்று: ஒரு செங்கோண முக்கோணத்தின் செம்பக்கம் அம்முக்கோணத்தின் சுற்றுவட்டத்தின் விட்டமாகும்.

தேலேசுத் தேற்றம் மற்றும் அதன் மறுதலை இரண்டையும் சேர்த்துப் பின்வரும் கூற்றை அமைக்கலாம்:

ஒரு முக்கோணம் செங்கோண முக்கோணமாக இருந்தால், இருந்தால் மட்டுமே, அம்முக்கோணத்தின் சுற்றுவட்ட மையம் அதன் ஏதேனும் ஒரு பக்கத்தின் மேல் அமையும்.

வடிவவியலைப் பயன்படுத்தி மறுதலையை நிறுவல்[தொகு]

\angle ABC

-ஒரு செங்கோணம்., A வழியாக BC -க்கு இணையாக வரையப்பட்ட கோடு r. C வழியாக AB -க்கு இணையாக வரையப்பட்ட கோடு கோடுகள் r , s இரண்டும் வெட்டும் புள்ளி D. ( D புள்ளி வட்டத்தின் மீது அமையும் என்பது நிறுவப்படவில்லை என்பதை கவனத்தில் கொள்க.)

நாற்கரம் ABCD -இன் எதிர்பக்கங்கள் இணையாக அமைவதால் அது ஒரு இணைகரம்.

ஒரு இணைகரத்தில் அடுத்துள்ள இருகோணங்கள் மிகைநிரப்புக் கோணங்கள்.

மேலும் $\angle ABC$ = $90^{\circ }$

ஃ $\angle BAD$ , $\angle BCD$ , $\angle ADC$ மூன்றும் செங்கோணங்கள்.

எனவே ABCD, ஒரு செவ்வகம்.

இதன் மூலைவிட்டங்கள் AC , BD வெட்டிக் கொள்ளும் புள்ளி O.

செவ்வகத்தின் பண்பின்படி புள்ளி O, புள்ளிகள் A, B, C -களிலிருந்து சமத் தொலைவில் இருக்கும்.

எனவே O , $\triangle ABC$ -இன் சுற்றுவட்டத்தின் மையமாகும். செம்பக்கம் அல்லது கர்ணம் AC, சுற்றுவட்டத்தின் விட்டமாகும்.

நேரியல் இயற்கணிதம் மூலமாக மறுதலையின் நிறுவல்[தொகு]

$\angle ABC$ , ஒரு செங்கோணம்.

AC -ஐ விட்டமாகக் கொண்ட வட்டம் M.

கணக்கீடு சுலபமாக இருப்பதற்கு M -இன் மையத்தை ஆதிப்புள்ளியாக எடுத்துக் கொள்ளவும்.

A = − C, ( ஏனெனில் வட்ட மையம் ஆதிப்புள்ளி; AC விட்டம்.)
(A − B) · (B − C) = 0, ( $\angle ABC$ செங்கோணம்.)

0 = (A − B) · (B − C) = (A − B) · (B + A) = |A|² − |B|².

எனவே:

|A| = |B|.

இதிலிருந்து A , B இரண்டும் ஆதியிலிருந்து அதாவது வட்டம் M -ன் மையத்திலிருந்து சமத் தொலைவில் அமையும் எனத் தெரிகிறது. A வட்டத்தின் மேல் அமைகிறது. ஆகவே B யும் வட்டத்தின் மேல் அமையும். $\triangle ABC$ -இன் மூன்று உச்சிகளும் வட்டம் M மீது அமைவதால் அது முக்கோணத்தின் சுற்றுவட்டமாகும்.

பொதுமைப்படுத்தல்[தொகு]

தேலேசுத் தேற்றத்தைப் பின்வரும் தேற்றத்தின் சிறப்பு வகையாகக் கருதலாம்:

O ஐ மையமாகக் கொண்ட வட்டத்தின் மீது அமையும் மூன்று புள்ளிகள் A,B,C எனில்

\angle AOC

-இன் அளவு

\angle ABC

-இன் அளவைப்போல் இருமடங்காகும்.

\angle AOC

= 2

\angle ABC

பயன்பாடுகள்[தொகு]

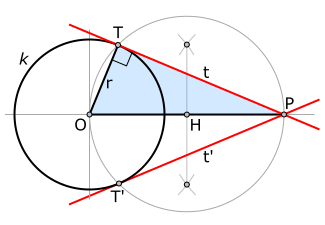
தேலேசு தேற்றத்தைப் பயன்படுத்தி தரப்பட்ட ஒரு வட்டத்திற்கு தரப்பட்ட ஒரு புள்ளியிலிருந்து தொடுகோடு வரையலாம்.

வரையும் முறை

தரப்பட்ட வட்டம் k. இதன் மையம் O.
தரப்பட்ட புள்ளி P வட்டத்திற்கு வெளியே அமைகிறது.
இப்புள்ளி வழியே வட்டத்திற்கு தொடுகோடு(சிவப்பு) வரைய வேண்டும்.
இன்னமும் வரையப்படாத தொடுகோடு t வட்டத்தைத் தொடும் புள்ளி T என்க.
சமச்சீர் பண்பின்படி ஆரம் OT தொடுகோட்டுக்குச் செங்குத்தாக இருக்கும்.
O மற்றும் P -ன் நடுப்புள்ளி H வரைதல் வேண்டும்.
H -ஐ மையமாகக் கொண்டு O மற்றும் P வழிச் செல்லும் வட்டம் ஒன்று வரைதல் வேண்டும்.
தேலேசு தேற்றப்படி இவ்வட்டமும் தரப்பட்ட வட்டமும் வெட்டும் புள்ளிதான்(T ) நமக்குத் தேவையான தொடுபுள்ளி.
ஏனெனில் இப்புள்ளிதான் O மற்றும் P -உடன் சேர்ந்து செங்கோணமுக்கோணத்தை முழுமையாக்குகிறது.
இரு வட்டங்கள் இரு புள்ளிகளில் வெட்டிக்கொள்ளும் என்பதால் இரு தொடுகோடுகள் வரையலாம்.

வரலாறு[தொகு]

தேலேசுக்கு முன்பே எகிப்திய மற்றும் பாபிலோனியர்கள் இத்தேற்றத்தின் கருத்தை அனுபவத்தில் அறிந்திருக்க வேண்டும் என்ற கருத்து உள்ளது. ஆனாலும் இத்தேற்றத்திற்கான எந்தவொரு நிறுவலும் அவர்களால் கண்டுபிடிக்கப்பட்டதற்கான ஆதாரங்கள் எதுவும் இல்லை. இத்தேற்றத்தை முதன்முதலில் நிறுவியவர் தாலேசு என்பதால் இத்தேற்றம் அவரது பெயரால் அழைக்கப்படுகிறது. தான் கண்டுபிடித்த, இருசமபக்க முக்கோணத்தின் அடிக்கோணங்கள் இரண்டும் சமமாக இருக்கும்; ஒரு முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் இரு செங்கோணங்களாகும் என்ற முடிவுகளைக் கொண்டு தாலேசு இத்தேற்றத்தினை நிறுவியுள்ளார்.

மேலும் பார்க்க[தொகு]

உள்வரைவு கோணத் தேற்றம்

மேற்குறிப்புகள்[தொகு]

Agricola, Ilka; Friedrich, Thomas (2008). Elementary Geometry. AMS. பக். 50. பன்னாட்டுத் தரப்புத்தக எண்:0821843478. (restricted online copy, p. 50, கூகுள் புத்தகங்களில்)
Thomas L. Heath (1921). A History of Greek Mathematics: From Thales to Euclid. I. Oxford. பக். 131ff.. http://www.archive.org/details/cu31924008704219.

வெளி இணைப்புகள்[தொகு]

Weisstein, Eric W., "Thales' Theorem", MathWorld.
Munching on Inscribed Angles
Thales' theorem explained With interactive animation
Thales' Theorem by Michael Schreiber, The Wolfram Demonstrations Project.
யூடியூபில் Les Luthiers - El Teorema de Thales (in spanish)