அணிக்கோவை

கணிதத்தில், நேரியல் இயற்கணிதப் பிரிவில் அணிக்கோவை அல்லது துணிகோவை (determinant) என்பது ஒவ்வொரு சதுர அணியுடனும் இணைக்கப்பட்ட ஒரு மதிப்பாகும். அச்சதுர அணியின் உறுப்புகள் ஒரு நேரியல் சமன்பாடுகளின் தொகுப்பின் குணகங்களாக இருக்கும்போது அந்த அணியின் அணிக்கோவையின் மதிப்பு பூச்சியமாக இல்லாமல் இருந்தால், இருந்தால் மட்டுமே (if and only if) அச்சமன்பாடுகளின் தீர்வு தனித்தன்மை வாய்ந்ததாக இருக்கும். அதேபோல அச்சதுர அணி ஒரு நேரியல் உருமாற்றத்தைக் குறிக்கும்போது அதன் அணிக்கோவையின் மதிப்பு பூச்சியமாக இல்லாமல் இருந்தால், இருந்தால் மட்டுமே அந்த உருமாற்றத்திற்கு நேர்மாறு உருமாற்றம் இருக்க முடியும்.

மெய்யெண் உறுப்புகளைக் கொண்ட ஒரு சதுர அணியின் அணிக்கோவை மதிப்பின் உள்ளுணர்வான விளக்கத்தைப் பின்வருமாறு தரலாம்:

ஒரு அணிக்கோவையின் தனி மதிப்பானது, அதன் அணி குறிப்பிடும் உருமாற்றத்தினால் மாறும் பரப்பின் (கன அளவு) பெருக்கத்தின் (குறுக்கம்) அளவைக் குறிக்கிறது. அணிக்கோவையின் குறியானது அந்த உருமாற்றத்தினால் அப்பரப்பின் (கனஅளவு) திசைப்போக்கு எவ்வாறு மாறுகிறது என்பதைக் குறிக்கிறது.^[1]^[2]^[3]

(அ-து) (- 2), மதிப்பு கொண்ட அணிக்கோவையின் அணிக்குரிய உருமாற்றமானது, தளத்தில் உள்ள எந்தவொரு வடிவினையும் இரு மடங்கு பரப்பும் எதிரான திசைப்போக்கும் உள்ள வடிவமாக உருமாற்றும்.

A என்ற அணியின் அணிக்கோவையின் குறியீடு, det(A) அல்லது அடைப்புக் குறியீடில்லாமல்: det Aஆகும். ஒரு அணியின் அணிக்கோவையை எழுதுவதற்கு, அவ்வணியின் அடைப்புக்குறிகளை நீக்கிவிட்டு அவற்றுக்குப் பதில் இரு செங்குத்துக் கோடுகளை இட வேண்டும்.

(அ-து)

{\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}}

என்ற அணியின் அணிக்கோவை:

${\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}$ .

வரையறை

ஒரு சதுர அணியின் அணிக்கோவை மதிப்பானது, அந்த அணியின் குறிப்பிட்ட உறுப்புகளின் பெருக்குத்தொகைகளை, ஒரு குறிப்பிட்ட விதிப்படிக் கூட்டிக் கழிப்பதால் கிடைக்கக் கூடிய ஒரு மதிப்பாகும். அந்த மதிப்பு, அணியின் உறுப்புகளாலான ஒரு பல்லுறுப்புக்கோவையாக அமையும். எனவே அணியின் வரிசை அதிகரிக்க அதிகரிக்க அக்கோவையில் உள்ள உறுப்புகளின் எண்ணிக்கையும் அதிகரிக்கும்.

(அ-து) n வரிசை உடைய அணியின் அணிக்கோவையின் மதிப்பு n! உறுப்புகள் கொண்ட பல்லுறுப்புக்கோவையாகும்.

n நிரைகளும் n நிரல்களும் கொண்ட அணி

A={\begin{bmatrix}a_{1,1}&a_{1,2}&\dots &a_{1,n}\\a_{2,1}&a_{2,2}&\dots &a_{2,n}\\\vdots &\vdots &\vdots &\vdots \\a_{n,1}&a_{n,2}&\dots &a_{n,n}\end{bmatrix}}.\,

மெய்யெண்களாகவோ அல்லது கோவைகளாகவோ அமையும் அணியின் உறுப்புகள், பரிமாற்றும் விதத்தில் ஒன்றாகக் கூட்டியும் பெருக்கவும் கூடியதாக இருப்பதைப் பொறுத்து, அணிக்கோவையின் வரையறை அமையும்.

A ன் அணிக்கோவை,

{\begin{vmatrix}a_{1,1}&a_{1,2}&\dots &a_{1,n}\\a_{2,1}&a_{2,2}&\dots &a_{2,n}\\\vdots &\vdots &\vdots &\vdots \\a_{n,1}&a_{n,2}&\dots &a_{n,n}\end{vmatrix}}\,

ஆகும்.

2 x 2 அணிகள்

2 x 2 அணியின் அணிக்கோவை,

{\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc\

என வறையறுக்கப்படுகிறது.

A அணியின் உறுப்புகள் மெய்யெண்களாக இருந்தால் அந்த அணி , இரு நேரியல் கோப்புகளைக் குறிப்பதாகக் கொள்ளலாம். ஒரு கோப்பு, திட்ட அடிப்படைத் திசையன்களை A ன் நிரைகளாகவும் மற்றொன்று A ன் நிரல்களாகவும் மாற்றும் கோப்புகளாகும். இரண்டிலுமே அடிப்படை வெக்டர்களின் பிம்பங்கள் ஒரு இணைகரத்தினை அமைக்கும்.இந்த இணைகரமானது இக்கோப்புகளின் கீழ் உருமாறிய ஓரலகு சதுரத்தின் பிம்பமாக அமையும்.

அணியின் நிரைகளால் அமையும் இணைகரத்தின் உச்சிப்புள்ளிகள், (0,0), (a,b), (a + c, b + d), மற்றும் (c,d). ad – bc ன் தனிமதிப்பு இணைகரத்தின் பரப்பாகும். மேலும் இம்மதிப்பு A ன் கீழ் உருமாறிய பரப்பின் மாற்றத்தின் அளவைக் குறிக்கும். (A ன் நிரல்களால் அமைக்கப்படும் இணைகரம் வேறாக இருந்தாலும் அணிக்கோவையானது நிரை, நிரலைப் பொறுத்த சமச்சீர்தன்மை (symmetry) கொண்டுள்ளதால் இரண்டு இணைகரங்களின் பரப்பும் சமமாகவே இருக்கும்.)

அணிக்கோவையின் தனி மதிப்புடன் குறியினைச் சேர்க்கும் பொழுது அது இணைகரத்தின் திசைப்போக்குடைய பரப்பினைக் குறிக்கிறது. திசைப்போக்குடைய பரப்பு என்பது வழக்கமான வடிவவியல் பரப்புதான். ஆனால் இணைகரத்தை உருவாக்கும் இரு வெக்டர்களில் முதல் வெக்டரிலிருந்து இரண்டாவது வெக்டருக்கான கோணம் கடிகாரதிசைக்கு எதிர்த்திசையில் அமையும்போது மட்டும் பரப்பின் குறி, குறைக்குறியாக அமையும்.

எனவே அணிக்கோவையின் மதிப்பு, A அணியின் கீழ் அமையும் உருமாற்றத்தின் அளவையும் திசைப்போக்கையும் தருகிறது. அணிக்கோவையின் மதிப்பு 1 எனில் இந்த உருமாற்றமானது திசைமாறா சமபரப்பு உருமாற்றமாகிறது.

3 x 3 அணிகள்

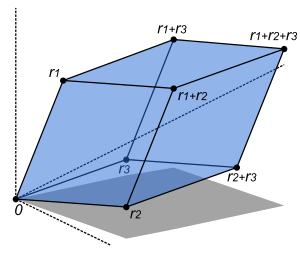
3×3 அணியின் அணிக்கோவை:

{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=aei+bfg+cdh-afh-bdi-ceg.\

இந்த சூத்திரத்திற்கான ஒரு சுருக்கு வழி, சாரஸ் விதியாகும் (sarrus rule).

இந்த விதிப்படி, படத்தில் உள்ளவாறு அணியின் மூன்று நிரைகளையும் நிரல்களையும் அதே வரிசையில் எடுத்துக்கொண்டு அதற்கு வலப்புறம் மீண்டும் முதல் இரு நிரல்களயும் எழுதிக்கொள்ள வேண்டும். பின்பு வடமேற்கு மூலைவிட்டங்களின் உறுப்புகளின் பெருக்குத்தொகைகளின் கூட்டுத்தொகையிலிருந்து, தென்கிழக்கு மூலைவிட்டங்களின் உறுப்புகளின் பெருக்குத்தொகைகளின் கூட்டுத்தொகையைக் கழித்தால் இந்த அணிக்கோவையின் மதிப்பு கிடைக்கும்.

இந்த சூத்திரம் மூன்றாம் வரிசை அணிக்கு மட்டுமே பொருந்தும். உயர்வரிசை அணிகளுக்குப் பொருந்தாது.

(எ.கா)

A={\begin{bmatrix}-2&2&3\\-1&1&3\\2&0&-1\end{bmatrix}}

எனில்,

$\det(A)\,$	$=\,$	$((-2)\cdot 1\cdot (-1))+(2\cdot 3\cdot 2)+(3\cdot (-1)\cdot 0)$
		$-\,(2\cdot 1\cdot 3)-(0\cdot 3\cdot (-2))-((-1)\cdot (-1)\cdot 2)$
	$=\,$	$2+12+0-6-0-2=6\,$

n x n அணிகள்

எல்லா வரிசையுடைய அணியின் அணிக்கோவையையும் லீபினிட்சு சூத்திரம் அல்லது லாப்லாசு சூத்திரத்தைப் பயன்படுத்திக் காணலாம்.

n x n அணி A ன் அணிக்கோவை காணப் பயன்படும் லீபினிட்சு சூத்திரம்:

\det(A)=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}A_{i,\sigma _{i}}.\

σ என்பது {1, 2, ..., n}. என்ற கணத்தின் வரிசைமாற்றங்களைக் குறிக்கும். வரிசைமாற்றம் என்பது முழுஎண்கணத்தின் வரிசைகளை மாற்றும் ஒரு கோப்பாகும். i என்ற உறுப்பின் இடவரிசை σ வினால் வரிசைமாற்றம் செய்யப்பட்டபின் σ_i எனக் குறிக்கப்படும். எடுத்துக்காட்டாக n = 3 எனில், 1, 2, 3 என்ற ஆரம்ப வரிசை S = [2, 3, 1], S₁ = 2, S₂ = 3, S₃ = 1 என வரிசைமாற்றம் செய்யப்படலாம் . அத்தகைய வரிசை மாற்றங்கள் அனைத்தும் கொண்ட கணத்தின் குறியீடு S_n. இக்கணம் n உறுப்புகளின் மீதான சமச்சீர் குலமாகும்.

sgn(σ) என்ற குறியீடு σ ன் குறியினைக் குறிக்கும். ஒவ்வொரு வரிசைமாற்றத்திற்கும் குறி (+ 1அல்லது - 1) உண்டு. σ ஒற்றை வரிசைமாற்றமாக இருந்தால் sgn(σ) ன் மதிப்பு – 1 ஆகவும் σ இரட்டை வரிசைமாற்றமாக இருந்தால் sgn(σ) ன் மதிப்பு + 1 ஆகவும் இருக்கும். மூலவரிசையிலிருந்து இரட்டை (ஒற்றை) எண்ணிக்கையிலான மாற்றங்களால் புதுவரிசைப் பெறப்படும்போது அந்த வரிசைமாற்றம், இரட்டை (ஒற்றை) வரிசைமாற்றம் எனப்படும். [1, 2, 3] → [2, 1, 3] → [2, 3, 1], என்பதில் மாற்றங்களின் எண்ணிக்கை இரண்டு என்பதால் இது இரட்டை வரிசைமாற்றம். [1, 2, 3] → [1, 3, 2] → [3, 1, 2] → [3, 2, 1] , என்பதில் மொத்த மாற்றங்கள் மூன்று என்பதால் இது ஒற்றை வரிசைமாற்றமாகும். ஒரு வரிசைமாற்றம் ஒரே சமயத்தில் இரட்டை மற்றும் ஒற்றை வரிசைமாற்றமாக இருக்க முடியாது.

\prod _{i=1}^{n}A_{i,\sigma _{i}}\

என்பது

A_{1,\sigma _{1}}\cdot A_{2,\sigma _{2}}\cdots A_{n,\sigma _{n}}.\

என்ற பெருக்குத்தொகையைக் குறிக்கும்.

எடுத்துக்காட்டாக, n = 3 எனில் அணி மூன்றாம் வரிசை அணியாகும்.

அதன் அணிக்கோவை லீபினிட்சு சூத்திரப்படி,

{\begin{aligned}\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}A_{i,\sigma _{i}}&=\operatorname {sgn}([1,2,3])\prod _{i=1}^{n}A_{i,[1,2,3]_{i}}+\operatorname {sgn}([1,3,2])\prod _{i=1}^{n}A_{i,[1,3,2]_{i}}+\operatorname {sgn}([2,1,3])\prod _{i=1}^{n}A_{i,[2,1,3]_{i}}\\&+\operatorname {sgn}([2,3,1])\prod _{i=1}^{n}A_{i,[2,3,1]_{i}}+\operatorname {sgn}([3,1,2])\prod _{i=1}^{n}A_{i,[3,1,2]_{i}}+\operatorname {sgn}([3,2,1])\prod _{i=1}^{n}A_{i,[3,2,1]_{i}}\\&=\prod _{i=1}^{n}A_{i,[1,2,3]_{i}}-\prod _{i=1}^{n}A_{i,[1,3,2]_{i}}-\prod _{i=1}^{n}A_{i,[2,1,3]_{i}}+\prod _{i=1}^{n}A_{i,[2,3,1]_{i}}+\prod _{i=1}^{n}A_{i,[3,1,2]_{i}}-\prod _{i=1}^{n}A_{i,[3,2,1]_{i}}\\&=A_{1,1}A_{2,2}A_{3,3}-A_{1,1}A_{2,3}A_{3,2}-A_{1,2}A_{2,1}A_{3,3}+A_{1,2}A_{2,3}A_{3,1}+A_{1,3}A_{2,1}A_{3,2}-A_{1,3}A_{2,2}A_{3,1}\end{aligned}}

இது சாரஸ் விதிப்படி கிடைக்கும் மதிப்பிற்குச் சமமானதாக உள்ளது.

அணிக்கோவையின் முக்கிய பண்புகள்

A ஒரு முக்கோண அணி எனில், (அ-து). a_i,j = 0, i > j அல்லது i < j
$\det(A)=a_{1,1}a_{2,2}\cdots a_{n,n}=\prod _{i=1}^{n}a_{i,i}\,$ ,
இது A அணியின் மூலைவிட்ட உறுப்புகளின் பெருக்கு தொகையாகும். எடுத்துக்காட்டாக முற்றொருமை அணி,
$\textstyle \mathrm {I} _{n}={\begin{bmatrix}1&0&\ldots &0\\0&1&\ldots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\ldots &1\end{bmatrix}}$ . இதன் அணிக்கோவை மதிப்பு 1.
A ன் நிரைகளை நிரல்களாகவும் நிரல்களை நிரைகளாகவும் பரிமாற்றம் செய்வதால் கிடைக்கும் அணி B எனில் det(B) = det(A).
A அணியின் ஏதாவது இரு நிரைகளைப் (நிரல்களை) பரிமாற்றம் செய்வதால் கிடைக்கும் அணி B எனில், det(B) = −det(A).
A அணியின் ஏதாவது ஒரு நிரையை (நிரலை) c என்ற எண்ணால் பெருக்கக் கிடைக்கும் அணி B எனில், det(B) = c · det(A). இதன் விளைவாக முழு அணியினை c ஆல் பெருக்கினால்,
$\det(cA)=c^{n}\det(A).\ \,$
A அணியின் ஏதாவது ஒரு நிரையின் (நிரலின்) மடங்கினை மற்றொரு நிரையோடு (நிரலோடு) கூட்டக்கிடைக்கும் அணி B எனில், $\det(B)=\det(A).\,$

இந்தப் பண்புகளை லீபினிட்சு சூத்திரத்தைப் பயன்படுத்திச் சரிபார்க்கலாம்.

இப்பண்புகளைப் பயன்படுத்தி எந்தவொரு அணியின் அணிக்கோவையின் மதிப்பைக் கணக்கிடலாம். இப்பண்புகளைப் பயன்படுத்தி ஒரு அணியை முக்கோண அணியாக எளிதில் மாற்றிப் பின் அதன் அணிக்கோவை மதிப்பைக் காணலாம்.

எடுத்துக்காட்டு:

A={\begin{bmatrix}-2&2&-3\\-1&1&3\\2&0&-1\end{bmatrix}}

எனில் பின்வரும் அணிகளைப்பயன்படுத்தி அதன் அணிக்கோவை மதிப்பைக் காணலாம்.

$B={\begin{bmatrix}-2&2&-3\\0&0&4.5\\2&0&-1\end{bmatrix}},C={\begin{bmatrix}-2&2&-3\\0&0&4.5\\0&2&-4\end{bmatrix}},D={\begin{bmatrix}-2&2&-3\\0&2&-4\\0&0&4.5\end{bmatrix}}$

A ன் இரண்டாம் நிரையோடு முதல் நிரையின் - 1/2 மடங்கினைக் கூட்டக் கிடைப்பது B அணி.

எனவே det(A) = det(B).

C என்பது B ன் முதல் நிரையோடு மூன்றாவது நிரையைக் கூட்டக்கிடைப்பது.

எனவே det(C) = det(B).

இறுதியாக, D என்பது C ன் இரண்டாவது, மூன்றாவது நிரைகளைப் பரிமாற்றக் கிடைப்பது.

எனவே det(D) = −det(C).

D என்பது மேல் முக்கோண அணியாக உள்ளது. எனவே அதன் அணிக்கோவையின் மதிப்பு அதன் முதன்மை மூலைவிட்ட உறுப்புகளின் பெருக்கலாகும்:

(−2) · 2 · 4.5 = −18.

ஃ det(A) = +18.

மேலும் சில பண்புகள்

$\det(A^{\mathrm {T} })=\det(A).\$

$\det(AB)=\det(A)\det(B).\$

$\det(A^{-1})={\frac {1}{\det(A)}}.$

லாப்லாசு சூத்திரமும் சேர்ப்பு அணியும்

லாப்லாசு சூத்திரம், ஓர் அணியின் சிற்றணிக்கோவைகள் மூலமாக அதன் அணிக்கோவையின் மதிப்பைக் காண பயன்படுகிறது.

சிற்றணிக்கோவை -M_i,j:

A அணியின் 'i-ஆம் நிரை மற்றும் j- ஆம் நிரலை நீக்குவதனால் கிடைக்கும் (n−1)×(n−1)- அணியின் அணிக்கோவையாகும்.

இணைக்காரணி -(C_i,j):

\mathbf {C} _{ij}=(-1)^{i+j}\mathbf {M} _{ij}.\,

அணி A -ன் அணிக்கோவை மதிப்பு:

\det(A)=\sum _{j=1}^{n}(-1)^{i+j}a_{i,j}M_{i,j}=\sum _{i=1}^{n}(-1)^{i+j}a_{i,j}M_{i,j}

இந்த வாய்ப்பாட்டின் மூலம் அணிக்கோவையின் மதிப்பைக் காண்பது அணிக்கோவையை ஒரு நிரை அல்லது நிரல் வழியாக விரிப்பதாகக் கருதப்படுகிறது.

(எ-கா)

மூன்றாம் வரிசை அணி,

$A={\begin{bmatrix}-2&2&-3\\-1&1&3\\2&0&-1\end{bmatrix}}$ , அணிக்கோவை மதிப்பினை லாப்லாசு விரிவின்படி இரண்டாவது நிரல் வாயிலாக விரிக்கக் கிடைப்பது:

$\det(A)\,$	$=\,$	$(-1)^{1+2}\cdot 2\cdot \det {\begin{bmatrix}-1&3\\2&-1\end{bmatrix}}+(-1)^{2+2}\cdot 1\cdot \det {\begin{bmatrix}-2&-3\\2&-1\end{bmatrix}}+(-1)^{3+2}\cdot 0\cdot \det {\begin{bmatrix}-2&-3\\-1&3\end{bmatrix}}$
	$=\,$	$(-2)\cdot ((-1)\cdot (-1)-2\cdot 3)+1\cdot ((-2)\cdot (-1)-2\cdot (-3))$
	$=\,$	$(-2)\cdot (-5)+8=18.\,$

எனினும் லாப்லாசு வாய்ப்பாடு சிறிய அணிகளுக்குத்தான் பலனுள்ளதாக இருக்கும்.

A ன் சேர்ப்பு அணி - adj(A):

A அணியின் இணைக்காரணிகளால் அமைந்த அணியின் நிரை-நிரல் மாற்று அணியாகும்.

(\operatorname {adj} (A))_{i,j}=(-1)^{i+j}M_{j,i}.\,

, மேலும்,

A\,\mathrm {adj} (A)=\mathrm {adj} (A)\,A=\det(A)\,I_{n}\qquad ,

கிராமரின் விதி

கிராமரின் விதிப்படி,

Ax=b\,

என்ற அணிச் சமன்பாட்டின் தீர்வு:

x_{i}={\frac {\det(A_{i})}{\det(A)}}\qquad i=1,\ldots ,n\,

இங்கு A_i என்பது, அணி A -ன் i -ஆம் நிரலுக்குப் பதில் நிரல் வெக்டர் b -ஐப் பிரதியிடுவதால் கிடைக்கும் அணியாகும்.

உசாத்துணை

Axler, Sheldon Jay (1997), Linear Algebra Done Right (2nd ed.), Springer-Verlag, ISBN 0387982590
de Boor, Carl (1990), "An empty exercise" (PDF), ACM SIGNUM Newsletter, 25 (2): 3–7, doi:10.1145/122272.122273.
Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0321287137
Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0898714548, archived from the original on அக்டோபர் 31, 2009, retrieved செப்டம்பர் 2, 2011 {{citation}}: Check date values in: |accessdate= (help)
Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3
Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall

வெளி இணைப்புகள்

WebApp to calculate determinants and descriptively solve systems of linear equations பரணிடப்பட்டது 2014-02-21 at the வந்தவழி இயந்திரம்
Determinant Interactive Program and Tutorial
Online Matrix Calculator
Linear algebra: determinants. பரணிடப்பட்டது 2008-12-04 at the வந்தவழி இயந்திரம் Compute determinants of matrices up to order 6 using Laplace expansion you choose.
Matrices and Linear Algebra on the Earliest Uses Pages
Determinants explained in an easy fashion in the 4th chapter as a part of a Linear Algebra course. பரணிடப்பட்டது 2009-05-25 at the வந்தவழி இயந்திரம்
Instructional Video on taking the determinant of an nxn matrix (Khan Academy) பரணிடப்பட்டது 2010-03-25 at the வந்தவழி இயந்திரம்
Online matrix calculator (determinant, track, inverse, adjoint, transpose) பரணிடப்பட்டது 2011-07-18 at the வந்தவழி இயந்திரம் Compute determinant of matrix up to order 8

↑ Lang 1985, §VII.1
↑ Wildberger, Norman J. (2010). Episode 4 (video lecture). WildLinAlg. Sydney, Australia: University of New South Wales. Archived from the original on 2021-12-11 – via YouTube.
↑ "Determinants and Volumes". textbooks.math.gatech.edu. Retrieved 16 March 2018.

[1] Lang 1985, §VII.1

[2] Wildberger, Norman J. (2010). Episode 4 (video lecture). WildLinAlg. Sydney, Australia: University of New South Wales. Archived from the original on 2021-12-11 – via YouTube.

[3] "Determinants and Volumes". textbooks.math.gatech.edu. Retrieved 16 March 2018.

[1]

[2]

[3]