பேஜ் தரவரிசை
இக்கட்டுரை கூகுள் மொழிபெயர்ப்புக் கருவி மூலம் உருவாக்கப்பட்டது. இதனை உரை திருத்த உதவுங்கள். இக்கருவி மூலம்
கட்டுரை உருவாக்கும் திட்டம் தற்போது நிறுத்தப்பட்டுவிட்டது. இதனைப் பயன்படுத்தி இனி உருவாக்கப்படும் புதுக்கட்டுரைகளும் உள்ளடக்கங்களும் உடனடியாக நீக்கப்படும் |
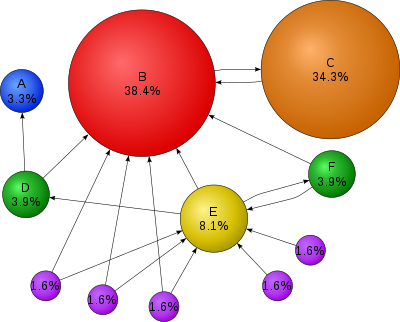
பேஜ் தரவரிசை (PageRank) என்பது லாரி பேஜ் (Larry Page) என்பவரின் பெயரால் உருவான ஒரு இணைப்புப் பகுப்பாய்வு செய்வழி ஆகும். இது உலகளாவிய வலை போன்ற மீ இணைப்பு (hyperlink) கொண்ட ஆவணங்களின் தொகுப்பின் ஒவ்வொரு தனிமத்திற்கும் ஒரு எண்ணிக்கை மதிப்பீட்டை வழங்கும் [1]கூகுள் இணைய தேடல் பொறியில் பயனாகிறது. இது ஒரு தொகுப்பிற்குள் இருக்கும் தழுவியல் முக்கியத்துவத்தை "அளவிடும்" நோக்கத்திற்காகப் பயன்படுகிறது. எதிரிடை கொண்ட குறிப்பீடுகள் மற்றும் மேற்கோள்கள் கொண்ட உட்பொருட்களின் ஆகிய எந்த சேகரிப்பிலும் இந்த செய்வழியினை இடலாம். கொடுக்கப்பட்ட ஒரு தனிமம் ஈ என்பதற்கு இது அளிக்கும் எண் மதிப்பீடு ஈயின் பேஜ் தரவரிசை எனவும் கூறப்படுகிறது. இதனை என்பது குறிக்கிறது.
"பேஜ் தரவரிசை" என்னும் இந்தப்பெயர் கூகுள் இணையத்தின் வர்த்தக முத்திரையாகும்; மேலும் இந்த பேஜ் தரவரிசை தனிக் காப்புரிமை கொண்டுள்ளது (U.S. Patent 62,85,999). எனினும், இந்த தனிக்காப்புரிமையானது கூகுளுக்கு அல்லாது ஸ்டான்ஃபோர்டு பல்கலைக்கழகத்திற்கே வழங்கப்பட்டுள்ளது. ஸ்டான்போர்டு பல்கலைக்கழகத்திடமிருந்து இந்த தனிக் காப்புரிமையின் தனி உரிமத்தை கூகுள் பெற்றுள்ளது.
இந்த தனிக் காப்புரிமை பயன்பாட்டிற்காக இப் பல்கலைக்கழகம் 1.8 மில்லியன் கூகிள் பங்குகளைப் பெற்றுள்ளது; இந்தப் பங்குகள் 2005ஆம் ஆண்டில் $336 மில்லியன்களுக்கு விற்கப்பட்டன.[2][3]
விவரிப்பு[தொகு]
பேஜ் தரவரிசையை கூகுள் இவ்வாறு விவரிக்கிறது:[4]
| “ | PageRank relies on the uniquely democratic nature of the web by using its vast link structure as an indicator of an individual page's value. In essence, Google interprets a link from page A to page B as a vote, by page A, for page B. But, Google looks at more than the sheer volume of votes, or links a page receives; it also analyzes the page that casts the vote. Votes cast by pages that are themselves "important" weigh more heavily and help to make other pages "important". | ” |
வேறு வார்த்தைகளில் சொல்ல வேண்டுமானால், பேஜ் தரவரிசை என்பது உலகளாவிய வலையில், ஒரு பக்கமானது மற்ற அனைத்துப் பக்கங்களுக்கும் மத்தியில் எந்த அளவு முக்கியமானதாக உள்ளது என்பதை ஒரு "வாக்களிப்பு" மூலம் அறிவதாகும். ஒரு பக்கத்திற்கு கொடுக்கப்படும் மீ இணைப்பு என்பது இதற்கு ஆதரவான வாக்காக கொள்ளப்படுகிறது.
ஒரு பக்கத்தின் பேஜ் தரவரிசை மீள்வரு என வரையறுக்கப்படுகிறது; மேலும் இது எண்ணைப் பொறுத்தும் மற்றும் இதனுடன் இணைப்பு கொண்ட ("உள் வரும் இணைப்புகள்") அனைத்துப் பக்கங்களின் பேஜ் தரவரிசை மீட்டர் முறையைப் பொறுத்தும் இருக்கிறது. உயர் பேஜ் தரவரிசை கொண்ட பக்கங்களுடன் இணையும் ஒரு பக்கமும் உயர் தரவரிசையைப் பெறுகிறது. ஒரு வலைப் பக்கத்திற்கு இணைப்புகள் ஏதும் இல்லையெனில், அந்தப் பக்கத்திற்கு ஆதரவு இல்லை என்று பொருளாகும்.
இணையத்தில் ஒவ்வொரு வலைப்பக்கத்திற்கும் பூஜ்யத்திலிருந்து பத்து வரையிலான எண் மதிப்பீடு ஒன்றை கூகுள் அளிக்கிறது; இந்த பேஜ் தரவரிசையானது, கூகுளின் பார்வையில் ஒரு தளத்தின் முக்கியத்துவத்தைக் குறிக்கிறது. பேஜ் தரவரிசை என்பது ரிச்டர் அளவுகோலைப் (Richter Scale) போல மடக்கை அளவுகோலில் உள்ள ஒரு கோட்பாட்டு நிகழ்தகவு மதிப்பிலிருந்து பெறப்பட்டதாகும். ஒரு குறிப்பிட்ட பக்கத்தின் பேஜ் தரவரிசை என்பது உட்பிணைப்பு இணைப்புகளின் எண்ணிக்கை மற்றும் இணைப்புகளை வழங்கும் பக்கங்களின் பேஜ் தர வரிசை ஆகியவற்றின் அடிப்படையில் அமைவதாகும். ஒரு பக்கத்தில் தேடப்படும் வார்த்தைகளின் தொடர்பு மற்றும் அந்தப் பக்கத்திற்கு உண்மையில் செல்வதை அறிவிக்கும் கூகுள் கருவிப்பட்டையின் எண்ணிக்கை போன்ற மற்ற காரணிகளும் பேஜ் தரவரிசையின் மதிப்பீட்டைப் பாதிப்பன என்பது முன்னரே அறிந்ததே. கையாடுதல், கேலிப்பொருளாக்குதல் மற்றும் மோசடி செய்தல் ஆகியவற்றைத் தவிர்ப்பதற்காக, பேஜ் தரவரிசையை மற்ற காரணிகள் எந்த அளவிற்குப் பாதிக்கின்றன எனத் தெளிவாகக் குறிப்பிடும் விபரங்களை கூகுள் அளிப்பதில்லை.
பேஜ் மற்றும் பிரின்னின் மூலக் கட்டுரை வந்ததிலிருந்து பேஜ் தரவரிசையைப் பற்றி எண்ணற்ற கல்விசார் கட்டுரைகள் பிரசுரமாகியுள்ளன.[5] நடைமுறையில், பேஜ் தரவரிசைக் கருத்தாக்கம் சூழ்ச்சிக் கையாளுமைக்கு வழுபாடு உடையதாக நிரூபணம் ஆகியுள்ளது. மேலும் பொய்யாக உயர்த்தப்பட்ட பேஜ் தரவரிசையைக் கண்டறியவும், அப்படி பொய்யாக உயர்த்தப்பட்ட பேஜ் தரவரிசை உடைய ஆவணங்களுடனான இணைப்பை பொருட்படுத்தாதிருக்க வழிகளைக் கண்டறியவும் பரந்துபட்ட தீவிரமான ஆராய்ச்சி மேற்கொள்ளப்பட்டுள்ளன.
இணையத்திற்கான மற்ற இணைப்பு-சார்ந்த மதிப்பீட்டு செய்வழிகளில் (டியோமாவாலும் தற்போது ஆஸ்க்.காம் என்பதாலும் பயன்படுத்தப்படும்)ஜான் க்ளெய்ன்பெர்க் (Jon Kleinberg) என்பவரால் கண்டுபிடிக்கப்பட்ட மோதற் செய்வழி (HITS algorithm), ஐபிஎம்மின் அறிவுசார் செயற்திட்டம் (IBM CLEVER project) மற்றும் நம்பிக்கைத் தரவரிசை செய்வழி (TrustRank algorithm) ஆகியவை அடங்கும்.
வரலாறு[தொகு]
பேஜ் தரவரிசை என்பதனை ஸ்டான்போர்ட் பல்கலைக்கழகத்தில் லேரி பேஜ் என்பவரும் (இதனால் தான் பேஜ் -தரவரிசை[6] என்று இது பெயர் பெற்றது) பின்னர் ஸெர்ஜி பிரின் என்பவரும் ஒரு புதிய வகை தேடல் பொறியைப் பற்றிய ஆராய்ச்சித் திட்டத்தின் ஒரு பகுதியாக உருவாக்கினர்.
பேஜ் தரவரிசை மற்றும் கூகுள் தேடல் பொறியின் முதல் மாதிரியைப் பற்றி விவரிக்கும் இந்தத் திட்டத்தைப் பற்றிய முதற் கட்டுரை 1998ஆம் ஆண்டு பிரசுரமானது[5]. இதற்குச் சிறிது காலத்திலேயே, பேஜ் மற்றும் பிரின் கூகுள் தேடல் பொறியின் நிறுவனமான கூகுள் இங்க்கினைத் துவக்கினர். கூகுள் தேடல் விளைவுகளின் மதிப்பீட்டை நிர்ணயிக்கும் பல காரணக்கூறுகளில் ஒன்றுதான் என்ற போதிலும் பேஜ் தரவரிசை கூகுள் இணையத்தின் தேடல் கருவிகள் அனைத்திற்குமான அடிப்படையைத் தொடர்ந்து அளிக்கிறது.[4]
1950ஆம் ஆண்டுகளில் பென்ஸில்வேனியா பல்கலைக்கழகத்தில் யூஜீன் கார்ஃபீல்ட் (Eugene Garfield) என்பவர் உருவாக்கிய மேற்கோள் காட்டல் பகுப்பாய்வு மற்றும் படுவா பல்கலைக்கழகத்தில் மாஸ்ஸிமோ மார்சியோரி (Massimo Marchiori) உருவாக்கிய மிகு தேடல் (Hyper Search) ஆகியவற்றின் பாதிப்பை பேஜ் தரவரிசை கொண்டுள்ளது. (கூகுளைத் துவங்கியோர் கார்பீல்ட் மற்றும் மார்சியோரியின் படைப்புகளைத் தங்களது மூலக் கட்டுரையில் மேற்கோள் காட்டியுள்ளனர்.[5]) பேஜ் தரவரிசை அறிமுகப்படுத்தப்பட்ட அதே வருடத்தில் (1998), ஜான் க்ளெய்பெர்க் மோதல்கள் (HITS) என்பதன் மீதான தனது முக்கியமான ஒரு படைப்பைப் பிரசுரித்தார்.
ஹார்வார்ட் பொருளாதார நிபுணரும் மற்றும் 1973ஆம் ஆண்டின் நோபல் பரிசு பெற்றவருமான வாஸ்ஸிலி லியான்டைஃப் (Wassily Leontief) 1941ஆம் ஆண்டு அளித்த ஒரு கட்டுரை, 2010ஆம் வருடத்தில் பேஜ் தரவரிசையின் பல் செயலாற்றும் வழிமுறையின் துவக்ககால அறிவுசார் முன்னோடியாக அங்கீகாரம் பெற்றது.[7][8][9]
செய்வழி[தொகு]
இணைப்புகளை அங்கொன்றும் இங்கொன்றுமாய் அழுத்தும் ஒருவர் ஒரு குறிப்பிட்ட பக்கத்திற்கு வரக்கூடிய வாய்ப்புகளைப் பற்றித் தெரியப்படுத்தும் ஒரு நிகழ்தகவு வியாபகம் தான் பேஜ் தரவரிசை என்பதாகும். ஆவண சேகரிப்பு எந்த அளவினதாயினும் அதன் பேஜ் தரவரிசையைக் கணக்கிட இயலும். ஒரு கணிப்பு முறைவழியின் தொடக்கத்தில் ஒரு சேகரிப்பில் உள்ள அனைத்து ஆவணங்களுக்கும் இந்த நிகழ்தகவு சமமாக பகிர்ந்தளிக்கப்படுகிறது என்று பல ஆராய்ச்சிக் கட்டுரைகள் அனுமானிக்கின்றன. பேஜ் தரவரிசைக் கணிப்புகளுக்கு சேகரிப்புகளின் ஊடாக “பல் செயலாற்றம்” எனப்படும் பல கடவுகள் தேவைப்படுகின்றன. இது ஏறத்தாழ்வான பேஜ் தரவரிசை மதிப்புக் கோட்பாடுகளின் உண்மை மதிப்பை மேலும் அதிக அளவில் முறையாகப் பிரதிபலிப்பதற்காகப் பயன்படுகிறது.
ஒரு நிகழ்தவு என்பதானது 0 மற்றும் 1 என்பதற்கு இடையில் ஒரு எண் மதிப்பீடாக அறிவிக்கப்படுவதாகும். ஒரு 0.5 நிகழ்தகவு என்பது ஒரு நிகழ்வு மெய்ப்படுவதற்கு "50% சாத்தியக்கூறு" கொண்டுள்ளது எனப் பொருள்படும். எனவே, 0.5 என்னும் பேஜ் தரவரிசை என்பது ஒருவர் முறைமையற்ற இணைப்புகளை அமுக்கும் பொழுது 0.5 பேஜ் தரவரிசை உள்ள ஒரு ஆவணத்திற்கு செலுத்தப்படுவதன் வாய்ப்புகள் 50% இருக்கும் என்று குறிக்கும்.
எளிமையாக்கப்பட்ட செய்வழி[தொகு]

ஏ , பி , சி மற்றும் டி என்னும் நான்கு இணைய பக்கங்களைக் கொண்ட ஒரு சிறிய அண்டம் இருப்பதாகக் கருதுங்கள். பேஜ் தரவரிசையின் முதல் தோராய மதிப்பீடு நான்கு ஆவணங்களுக்கும் சமமாகப் பகிர்ந்து கொடுக்கப்படும். எனவே, ஒவ்வொரு ஆவணமும் 0.25 என கணக்கிடப்பட்ட பேஜ் தரவரிசையுடன் தொடங்கும்.
பேஜ் தரவரிசையின் மூலப் படிவத்தின்படி முதல் மதிப்புகள் வெறும் 1 என இருந்தன. எல்லாப் பக்கங்களின் கூட்டுத் தொகை என்பது வலையில் உள்ள பக்கங்களின் மொத்த எண்ணிக்கையாக இருக்கும் என்பது இதன் பொருளாகும். பேஜ் தரவரிசையின் பிற்பாடு வந்த பதிப்புகள் (கீழே கொடுக்கப்பட்டுள்ள விதிமுறைகளை காண்க) நிகழ்தகவு பரவலை 0 மற்றும் 1 என்பதற்கு இடைப்பட்டதாக கருதும். இங்கு ஒரு எளிமையான நிகழ்தகவு பரவல் பயன்படுகிறது- எனவே தொடக்க மதிப்பு 0.25 என்பதாக இருக்கும்.
பக்கங்கள் பி , சி மற்றும் டி ஒவ்வொன்றும் ஏ பக்கத்துடன் மட்டும் தொடர்பு கொண்டால், அவை ஒவ்வொன்றும் 0.25 பேஜ் தரவரிசையை ஏ பக்கத்திற்கு அளிக்கிறது. எல்லா இணைப்புகளும் ஏ யை நோக்கி இருப்பதால், இந்த எளிமையான செயல்பாட்டில் எல்லா பேஜ் தர வரிசைகளும் பிஆர்() ஏ யிடம் வந்து சேரும்.
இது 0.75 ஆகும்.
மீண்டும், பி பக்கமானது சி பக்கத்துடன் இணைப்பும், மற்றும் டி பக்கம் எல்லா மூன்று பக்கங்களுடனும் இணைப்பும் கொண்டிருப்பதாக வைத்துக் கொள்ளுங்கள். ஒரு பக்கத்தின் அனைத்து வெளியில் செல்லும் இணைப்புகளுக்கும் சமமாக இந்த இணைப்பு-வாக்குகளின் மதிப்பு பகிர்ந்தளிக்கப்படும் . இவ்வாறு, பக்கம் பி 0.125 மதிப்புள்ள வாக்கு ஒன்றை ஏ பக்கத்திற்கும் 0.125 மதிப்புள்ள வாக்கு ஒன்றை சி பக்கத்திற்கும் அளிக்கிறது. ஏயின் பேஜ் தரவரிசைக்கு டி 'யின் பேஜ் தரவரிசையில் மூன்றில் ஒரு பாகமே கணக்கில் கொள்ளப்படுகிறது (ஏறத்தாழ 0.083).
இதையே பிற சொற்களில் கூறுவதானால், ஒரு வெளியில் செல்லும் இணைப்புக்கு வழங்கப்படும் பேஜ் தரவரிசை, ஒரு ஆவணத்தின் சொந்த பேஜ் தர வரிசையின் மதிப்பு சாதாரணமான எண்ணிக்கை கொண்ட வெளியில் செல்லும் இணைப்புகள் எல் ( ) லால் வகுக்கப்படுவதற்கு சமமாக இருக்கும் (குறிப்பிட்ட யூஆர்எல்களுக்கான இணைப்புகள் ஒரு ஆவணத்திற்கு ஒரு முறை மட்டுமே கணக்கெடுக்கும் என்று கருதப்படுகிறது).
பொதுப்படையான நேரங்களில், எந்தவொரு பக்கத்திற்குமான பேஜ் தரவரிசையான யு என்பதை கீழ்க்கண்டவாறு வெளிப்படுத்தலாம்:
,
அதாவது, யு என்னும் பக்கத்தின் பேஜ் தரவரிசை மதிப்பு, பியு என்னும் தொகுதியில் உள்ள ஒவ்வொரு வி பக்கத்தின் பேஜ் தரவரிசையும் பக்கம் வி யிலிருந்து வரும் இணைப்புகளிலிருந்து வரும் எண்ணிக்கை எல் வி என்பதால் வகுக்கப்பட்ட தொகையை சார்ந்து உள்ளது (பக்கம் யு வுடன் இணையும் அனைத்துப் பக்கங்களும் இந்தத் தொகுதியில் உள்ளன).
தணிவிக்கும் காரணி[தொகு]
இணைப்புகளை அங்கொன்றும் இங்கொன்றுமாய் அழுத்தும் ஒரு கற்பனையான உலாவர் கூட ஒரு குறிப்பிட்ட சமயத்தில் அழுத்துவதை நிறுத்திவிடுவார் என பேஜ் தரவரிசைக் கோட்பாடு கூறுகிறது. எந்த ஒரு கட்டத்திலும் அந்த நபர் இதைத் தொடர்வார் என்னும் நிகழ்தகவானது டி என்னும் ஒரு தணிவிக்கும் காரணியாகிறது. பல்வேறு ஆய்வுகள் பலவித தணிவிக்கும் காரணிகளைச் சோதித்திருக்கின்றன. ஆயினும், பொதுவாக தணிவிக்கும் காரணியானது 0.85 என்பதைச் சுற்றியே அமையும் எனக் கருதப்படுகிறது.[5]
இந்த தணிவிக்கும் காரணி 1 என்பதிலிருந்து கழிக்கப்படுகிறது (மேலும் செய்வழியின் சில வேறுபாடுகளில் இந்த விடை சேகரிப்பில் உள்ள ஆவணங்களின் எண்ணிக்கை என் என்பதால் வகுக்கப்படுகிறது). இந்தப் பதம் பின்னர் தணிவிக்கும் காரணி மற்றும் உள்வரும் பேஜ் தரவரிசை மதிப்புகளின் கூட்டுத்தொகை ஆகியவற்றின் பெருக்கத் தொகையுடன் கூட்டப்படுகிறது. அதாவது,
எனவே, எந்தவொரு பக்கத்தின் பேஜ் தரவரிசையும் பெரும்பாலும் மற்ற பக்கங்களின் பேஜ் தரவரிசையிலிருந்து வருவிக்கப்படுகிறது. தணிவிக்கும் காரணியானது, வருவிக்கப்பட்ட மதிப்பீட்டை கீழாகச் சரி செய்யும். எனினும், மூலப் பதிப்பானது சற்றே மாறுபட்ட ஒரு விதிமுறையை அளிக்கிறது. இது சற்றே குழப்பத்திற்குக் கொண்டு செல்வதாக உள்ளது.
இவற்றின் வேறுபாடு என்பது முதல் விதிமுறையில் பேஜ் தரவரிசையின் மதிப்புகளின் கூட்டுத்தொகை ஒன்றாக இருக்கிறது. ஆனால் இரண்டாவது முறையில் ஒவ்வொரு பேஜ் தரவரிசையும் என் என்பதால் பெருக்கப்பட்டு அதன் கூட்டுத்தொகை என் என்பதாகிறது; இதுவே இதில் உள்ள வித்தியாசம் ஆகும். பேஜ் மற்றும் பிரின்னின் கட்டுரையில் உள்ள "அனைத்து பேஜ் தர வரிசைகளின் கூட்டுத்தொகையும் ஒன்று"[5] என்னும் வாசகமும் மற்ற கூகுள் பணியாளர்களின்[10] கூற்றும் மேலே கொடுக்கப்பட்டுள்ள விதிமுறையின் முதல் மாற்றுருவை ஆதரிக்கிறது.
வலையில் தவழும் ஒவ்வொரு முறையும் கூகுள் பேஜ் தரவரிசையை மறு கணக்கீடு செய்து தனது பொருளடக்க அட்டவணையை மறுபடி உருவாக்குகிறது. தனது சேகரிப்பில் ஆவணங்களை கூகுள் உயர்த்தும் பொழுது, அனைத்து ஆவணங்களுக்கும் தொடக்கத்தில் கொடுக்கப்பட்ட ஒத்த பேஜ் தரவரிசை குறைகிறது.
இந்த விதிமுறை பல முறை அழுத்திய பின்பு சலித்து ஏதோ ஒரு பக்கத்திற்கு செல்லும் ஒரு முறைமையற்ற உலாவர் என்னும் மாதிரியைப் பயன்படுத்துகிறது. அந்த முறைமையற்ற உலாவர் ஒரு இணைப்பை அழுத்தும் பொழுது குறிப்பிட்ட பக்கத்தை அடையும் வாய்ப்பை ஒரு பக்கத்தின் பேஜ் தரவரிசை பிரதிபலிக்கிறது. இதை மார்கோவ் சங்கிலி (Markov chain) எனவும் புரிந்து கொள்ளலாம்; இதில் நிலைகள் பக்கங்களாகவும், மாற்றல்கள் சமமாக நிகழக்கூடியதாயும் அவையே பக்கங்களின் இடையில் இருக்கும் இணைப்புகளாகவும் உள்ளன.
ஒரு பக்கத்தில் மற்ற பக்கத்திற்கு இணைப்புகள் இல்லாதிருந்தால், அது தேங்கிடமாகிறது; அதனால் அது முறைமையற்ற செயல்பாட்டை முடிவுக்கு கொண்டு வருகிறது. எனினும், இதற்கான தீர்வு மிகவும் எளிமையானது. ஒரு முறைமையற்ற உலாவர் தேக்கமான ஒரு பக்கத்திற்கு வந்தால், அது மற்றொரு யூஆர்எல்லைத் தொடர்பில்லாமல் எடுத்துக் கொண்டு மறுபடியும் தேடத் தொடங்கி விடுகிறது.
பேஜ் தரவரிசையைக் கணக்கிடும்போது, வெளியில் செல்லும் இணைப்புகள் ஏதுமில்லாத பக்கங்கள் அந்த சேகரிப்பில் மற்ற அனைத்து பக்கங்களுக்கும் இணைப்பு கொடுப்பதாகக் கருதப்படுகிறது. இதனால் இவற்றின் பேஜ் தரவரிசை மதிப்பு மற்ற அனைத்து பக்கங்களுக்கும் சமமாக பகிர்ந்தளிக்கப்படுகிறது. அதாவது, தேக்க நிலை அற்ற மற்ற பக்கங்களுக்கும் நியாயம் வழங்க, சராசரியான ஒரு உலாவர் தனது உலாவியின் பக்கக்குறிப்பு அம்சத்தைப் பயன்படுத்துவார் என்னும் அலை அதிர்வெண்ணைக் கொண்டு கணக்கிட்டு, டி = 0.85 என்னும் எச்ச நிகழ்தகவோடு இந்த முறைமையல்லாத மாற்றல்கள் வலையின் அனைத்துக் கணுக்களுடனும் கூட்டப்படுகிறது.
எனவே, இந்தச் சரியீடு கீழ்க்கண்டவாறு அமைகிறது:
கருத்தில் கொள்ளப்படும் பக்கங்கள் வாக இருக்குமிடத்தில், யுடன் இணைக்கும் பக்கங்களின் தொகுதி ஆகும், பக்கத்தில் இருக்கும் வெளியில் செல்லும் இணைப்புகள் ஆகும், மேலும் என் என்பது பக்கங்களின் மொத்த எண்ணிக்கை ஆகும்.
மேம்படுத்தப்பட்ட அடுத்துள்ள அணியின் பிரதானமான எய்ஜென் திசையன் (eigenvector) பதிவுகள் பேஜ் தரவரிசையின் மதிப்புகள் ஆகும். இது பேஜ் தரவரிசையை ஒரு குறிப்பான நேர்த்தியான மீட்டர் முறையாக்குகிறது: எய்ஜென் திசையன் என்பது
சரியீட்டின் தீர்வு ஆர் என்னுமிடத்தில்
பக்கம் என்பதை இணைக்காவிடில், அடுத்துள்ள சார்புலன் 0 என்பதாக இருக்குமிடத்தில், ஒவ்வொரு ஐ என்பதற்கும் சாதாரணமாக்கப்படுகிறது.
,
அதாவது ஒவ்வொரு வரிசையின் தனிமங்களின் கூட்டுத்தொகை 1 என்பதாக வரும். (மேலும் விவரங்களுக்கு கீழே கொடுக்கப்பட்டிருக்கும் கணிப்பு என்னும் பகுதியைக் காணவும்). இது வலையமைப்பு பகுப்பாய்வில் வழமையாகப் பயன்படுத்தப்படும் எய்ஜென் திசையன் மையத்தன்மை கணிப்பின் ஒரு மாறுபாடாகும்.
மேலே இருக்கும் மேம்படுத்தப்பட்ட அடுத்துள்ள அணியின் மிகப் பெரிய எய்ஜென் இடைவெளியால், [11] பேஜ் தரவரிசை எய்ஜென் திசையன்னின் மதிப்புகள் விரைவாக தோராயமாக்கப்படுகின்றன. (சில பல் செயலாற்றங்களே தேவைப்படுகின்றன).
மார்கோவ் கோட்பாட்டின் விளைவாக, பல அழுத்தங்களுக்குப் பின் அந்தப் பக்கத்திற்கு வரும் நிகழ்தகவே அந்தப் பக்கத்தின் பேஜ் தரவரிசை என்பதைக் காட்டலாம். எங்கு ஒரு பக்கத்திலிருந்து அதற்கே வருவதற்கு தேவையான எதிர்பார்க்கப்படும் அழுத்தங்களின் (அல்லது முறைமையற்ற தாவல்கள்) எண்ணிக்கை ஆக இருக்கிறதோ அங்கு க்கு நிகராக சரியீட்டுவது நிகழ்கிறது.
இதில் உள்ள முதன்மையான பாதிக்கும் நிலை என்னவென்றால், இது பழைய பக்கங்களுக்கே அதிகம் ஆதரவளிக்கிறது, ஏனெனில் ஒரு புதிய பக்கம் மிகவும் நன்றாக இருப்பினும், அது அப்பொழுது இருக்கும் ஒரு தளத்தின் பகுதியாக இல்லாத வரை அதிக இணைப்புகள் கொண்டிருக்காது. (விக்கிபீடியா போன்று அடர்ந்த இணைப்புகள் கொண்ட பக்கங்களின் தொகுதி ஒரு தளம் எனவாகும்). கூகுள் அடைவு (இதுவே திறந்த அடைவுத் திட்டத்திலிருந்து பெறப்பட்டதாகும்) வகையினங்களுக்குள் விளைவுகள் பேஜ் தரவரிசையால் தரப்படுத்தப்பட்டிருப்பதைக் காண பயனர்களுக்கு அனுமதியளிக்கிறது. பேஜ் தரவரிசை நேரடியாக நிர்ணயிக்கும் காட்சியமைவு வரிசை இடம் பெறும் கூகுள் அடைவு ஒன்றே கூகுளால் அளிக்கப்படும் ஒரே சேவையாகும்.[சான்று தேவை] கூகுளின் (அதன் முதன்மை வலைத் தேடல் போன்ற) ஏனைய தேடல் சேவைகளில், தேடல் விளைவுகளில் காண்பிக்கப்படும் பக்கங்களின் தொடர்புடைய மதிப்புகளை எடையிட பேஜ் தரவரிசை பயன்படுகிறது.
பேஜ் தரவரிசையின் கணிப்பை முடுக்கி விடப் பல வழிமுறைகள் முன்மொழிந்துள்ளனர்.[12]
விளம்பர இணைப்புகளில் நிதி திரட்டவும் தேடல் விளைவுகளின் தரத்தை முன்னேற்றவும் பேஜ் தரவரிசையை திறமையாகக் கையாடவும் கூட்டு முயற்சியாகப் பல வழிமுறைகளை மேற்கொள்கின்ற்னர்.
எந்தெந்த ஆவணங்கள் உண்மையில் வலை சமூகத்தில் அதிக மதிப்பு பெறுகின்றன என்பதை நிர்ணயிக்க முயலும் பேஜ் தரவரிசை கருத்தின் நம்பகத்தன்மையை இந்த முறைமைகள் தீவிரமாக பாதிக்கின்றன.
பேஜ் தரவரிசையைச் செயற்கையாக உயர்த்துவதற்கு வடிவமைக்கப்பட்டிருக்கும் இணைப்புப் பண்ணைகள் மற்றும் மற்ற திட்டங்களை தண்டிப்பதில் கூகுள் பெயர் பெற்றுள்ளது. 2007ஆம் ஆண்டு டிசம்பர் மாதத்திலிருந்து கூகுள் இலவசமல்லாத மொழி இணைப்புகளை விற்கும் தளங்களை தண்டிப்பதை செயற்படுத்த த் துவங்கியது. எவ்வாறு இணைப்புப் பண்ணைகளையும் மற்ற பேஜ் தரவரிசையை கையாடும் கருவிகளையும் கூகுள் கண்டுபிடிக்கிறது என்பது அதன் வர்த்தக இரகசியத்தில் அடக்கம்.
கணக்கிடுதல்[தொகு]
சுருக்கமாகக் கூறுவதெனின், பேஜ் தரவரிசையினை பல் செயலாற்றலாலோ அல்லது இயற் கணித முறையிலோ கணக்கிடலாம். இதற்கு மாறாக, அடுக்கு பல் செயலாற்றும் முறை[9][13] அல்லது அடுக்கு முறை என்பதும் பயன்படலாம்.
பல் செயலாற்று[தொகு]
முதல் நிலையில், வில், ஒரு தொடக்க நிகழ்தகவு பகிர்தல் கருதப்படுகிறது,
- பொதுவாக அது
ஒவ்வொரு கால கட்டத்திலும், மேலே விவரிக்கப்பட்டுள்ளபடி அந்த கணிப்பு
என்பதனை அளிக்கிறது.
அல்லது அணி குறியீட்டில்
, (*) பின்வருமிடத்தில் மற்றும் என்பவை 1 என்னும் எண்ணிக்கைகள் மட்டுமே இருக்கும் நீளத்தின் வரிசைத் திசையன் ஆகும்.
அணியைப் பின்வருமாறு வரையறுக்கலாம்:
அதாவது,
, பின்வருமிடத்தில் என்பது வரைபடத்தின் அடுத்துள்ள அணியைக் குறிக்கிறது. மேலும் மூலை விட்டத்தில் வெளி நிலைப் படித்தரத்துடன் இருக்கும் மூலைவிட்ட அணி ஆகும்.
ஒரு சிறிய என்பதுடன் இந்த கணிப்பு முடிகிறது:
, அதாவது, குவிதல் என்பது அனுமானமாக இருக்கையில் இவ்வாறு நிகழ்கிறது.
இயற் கணித முறை[தொகு]
பிந்தைய நிலையில், ற்கு(அதாவது, உறுதியான நிலையில்) மேற்சொன்ன சரியீடு (*) இவ்வாறு பொருள் கொள்கிறது.
. (**) இதற்கான தீர்வு பின் வருமாறு
, முற்றொருமை அணியுடன் அளிக்கப்படுகிறது.
இதற்குத் தீர்வு உள்ளது மற்றும் இது என்பதற்குத் தனித்தன்மை கொண்டுள்ளது.
என்பது ஸ்டோகாஸ்டிக் அணியின் உருவாக்கத்தால் விளைவது; எனவே பெர்ரான்-ஃப்ரோபெனியஸ் கோட்பாட்டினால் இதன் எய்ஜென் மதிப்பு ஒன்றுக்கு ஈடாக இருக்கிறது என்பதை நோக்கும் பொழுது இதை அறியலாம்.
அடுக்கு முறை[தொகு]
அணி ஒரு நிலை மாற்ற நிகழ்தகவாக இருந்தால், அதாவது, பூஜ்யங்கள் மட்டும் இருக்கும் எந்த வரிசையும் இல்லாத வரிசை ஸ்டோகாஸ்டிக் என இருந்தால், மேலும் என்பது ஒரு நிகழ்தகவு பகிர்தலானால் (அதாவது, ) (**) சரியீடு என்பது கீழே கொடுக்கப்பட்டுள்ளதற்கு இணைமாற்றாக இருக்கும்.
. (***) எனவே என்னும் பேஜ் தரவரிசை என்பதே ன் முதன்மை எய்ஜென் திசையன் ஆகும். இதை கணிப்பதற்கு ஒரு வேகமான மற்றும் சுலபமான வழி அடுக்கு முறையை பயன்படுத்துவதாகும். ஏதேனும் ஒரு திசையன் என்பதலிருந்து தொடங்கி, செயலி தொடர்ச்சியாக இடப்படுகிறது; அதாவது,
, கீழ்க்காண்பது வரும் வரையிலும்:
.
சரியீடு (***) என்பதில் அடைப்புக் குறிக்குள் வலது பக்கத்தில் இருக்கும் அணியை பின் வருமாறு பொருள் கொள்ளலாம் என்பதை குறித்துக் கொள்ளவும்.
, இங்கு ஒரு தொடக்க நிகழ்தகவு பரத்தல் ஆகும். நடப்பு நிலையில்
.
இறுதியாக, பூஜ்ய மதிப்புகள் மட்டும் இருக்கும் வரிசைகளைக் கொண்டிருந்தால், அவை தொடக்க நிகழ்தகவு திசையன்னால் மாற்றப்பட வேண்டும். இதனை வேறு சொற்களில் கூற வேண்டுமெனில், எங்கு
, அணி பின் வருமாறு வரையறுக்கப்பட்டுள்ளதோ, அங்கு
, என்பதுடன் இருக்கும்.
இந்த நிலையில், ஐ பயன்படுத்தும் மேலே கொடுக்கப்பட்டிருக்கும் இரண்டு கணிப்புகளுமே, அவற்றின் விளைவுகள் சாதாரணமாக்கப்பட்டால் ஒரே பேஜ் தரவரிசையைத் தான் கொடுக்கும்:
.
செயல்திறன்[தொகு]
கணிப்பதற்கு பயன்படுத்தும் பணிச்சட்டம், முறைகளின் சரியான செயல்பாடு மற்றும் விளைவின் தேவைப்படும் துல்லியம் ஆகியவற்றைப் பொறுத்து மூன்று முறைகளின் கணிப்பு நேரமும் வெகுவாக வேறுபடக் கூடும். வழமையாக கணிப்பு பல முறை செய்யப்பட வேண்டி இருந்தாலோ (அதாவது, வளர்ச்சியடையும் வலையமைப்புகளில்) அல்லது வலையமைப்பின் அளவு பெரியதாக இருந்தாலோ, இயற் கணித கணிப்பு மந்தமாகும்; மேலும் அணியின் நேர்மாற்றலால் நினைவகம் வறட்சியடையும்; அடுக்கு முறையே அதிக ஆற்றலுடையதாகும்.
வேறுபாடுகள்[தொகு]
கூகுள் கருவிப் பலகை[தொகு]
காணப்பட்ட ஒரு பக்கத்தின் பேஜ் தரவரிசையை கூகுள் கருவிப்பலகையின் பேஜ் தரவரிசை அம்சம் 0 என்பதிலிருந்து 10 என்பது வரையிலான ஒரு நிறைவெண்ணாகக் காட்டும். மிகவும் புகழ் வாய்ந்த வலைத் தளங்களின் பேஜ் தரவரிசை 10 என்பதாக இருக்கும். இதில் மிகவும் கீழான நிலையில் உள்ளது பேஜ் தரவரிசையை 0 என்பதாகக் கொண்டிருக்கும். ஒரு கருவிப்பலகை பேஜ் தரவரிசையின் மதிப்பை நிர்ணயிக்கும் சரியான முறையை முன்னர் கூகுள் வெளியிடவில்லை;
பின் வரும் ஒற்றைவரி ஜாவா எழுத்துரு யுஆர்எல் மாற்றைச் செயல்படுத்துகிறது. மேலும் எந்த மேலோடியின் அடையாளக்குறிப் பலகையிலும் (தற்போது கூகுள் கருவிப்பலகை செருகு இல்லாதிருக்கும் கூகுள் க்ரோமையும் உள்ளடக்கி) இதை ஒரு அடையாளக் குறியீடு என்பதாகப் பயன்படுத்தலாம்.
ஸெர்ப் தரவரிசை[தொகு]
ஸெர்ப் (தேடல் பொறியின் விளைவுகள் பக்கம்) என்பது ஒரு திறவுச் சொல் வினவலுக்கு விடையாக ஒரு தேடல் பொறி அளிக்கும் ஒரு உண்மை விளைவாகும். ஸெர்ப், துணுக்குகளுடன் கூடிய துணைப் பனுவல்களை உடைய வலைப் பக்கங்களிற்கான இணைப்புகளின் பட்டியலைக் கொண்டதாகும். ஒரு வலைப் பக்கத்தின் ஸெர்ப் தரவரிசை என்பது ஸெர்ப்பில் அதற்குரிய பொருத்தமான இணைப்புகளை இடுவதைக் குறிக்கிறது. இங்கு உயர்ந்த இடத்தில் வைக்கப்படுவதென்பது உயர்ந்த ஸெர்ப் தரவரிசை உடையது எனப் பொருள்படும். ஒரு வலைப் பக்கத்தின் ஸெர்ப் தரவரிசை என்பது அதன் பேஜ் தரவரிசையின் செயல்பாடு மட்டும் அல்லாது இதை விட பெரிய மற்றும் தொடர்ந்து சரி செய்யப்பட்ட காரணிகளின் தொகுதியைப் பொறுத்தும் இருக்கிறது;[14][15] ஆகியவற்றை இணைய வணிகர்கள் "கூகுள் காதல்" எனக் குறிப்பிடுகின்றனர்.[16]. ஒரு வலைத் தளத்திற்கோ அல்லது வலைப் பக்கங்களின் தொகுதிக்கோ இயன்ற அளவு உயர்ந்த ஸெர்ப் தரவரிசையை அடைவதே எஸ்ஈஓவின் (தேடல் பொறி உகப்பாக்கம்) குறிக்கோளாகும்.
கூகுள் அடைவு பேஜ் தரவரிசை[தொகு]
கூகுள் அடைவு பேஜ் தரவரிசை என்பது ஒரு எண்ம-அலகு அளவை. இதன் மதிப்புகளை கூகுள் அடைவில் காணலாம். பேஜ் தரவரிசையின் மதிப்பை பச்சைப் பலகையின் மேல் சுட்டியை நகர்த்துவதன் மூலம் காண்பிக்கும் கூகுள் கருவிப்பலகையைப் போல் அன்றி, கூகுள் அடைவு பேஜ் தரவரிசையை ஒரு எண் மதிப்பாக காண்பிக்காமல் ஒரு பச்சைப் பலகையாக மட்டுமே காண்பிக்கிறது.
போலியான அல்லது ஏமாற்றான பேஜ் தரவரிசை[தொகு]
அநேக தளங்களுக்கு, கருவிப்பலகையில் காண்பிக்கப்படும் பேஜ் தரவரிசை ஒரு துல்லியமான பேஜ்தர வரிசை மதிப்பிலிருந்து பெறப்பட்டதாக கருதப்பட்டாலும் (கூகுள் பிரசுரிக்கப்பட்ட காலத்திற்கு சில காலம் முன்னர்), இந்த மதிப்பானது எளிமையாகக் கையாடப்படக் கூடியது என்பதைக் கருத்தில் கொள்ள வேண்டும். ஒரு குறைந்த பேஜ் தரவரிசை உள்ள பக்கம் ஹெச்டிடிபி 302 துலங்கள் வழியாக அல்லது ஒரு "புது மலர்வு" மீ அடையாள ஓட்டு மூலம் உயர்ந்த பேஜ் தரவரிசை கொண்ட பக்கத்திற்கு திரும்பி அனுப்பப்படும் பொழுது அந்த இலக்குப் பக்கத்தின் உயர் பேஜ் தரவரிசையை இந்த குறைந்த பேஜ் தர வரிசை கொண்ட பக்கம் அடைந்து விடுமாறு செய்து விடுவது முன்னர் இருந்த ஒரு குறைபாடாகும். கோட்பாட்டின்படி, உள்வரும் இணைப்புகள் ஏதும் இல்லாத ஒரு 0 என்பதனைக் கொண்ட ஒரு புதிய பிஆர் (பேஜ் தரவரிசை) பக்கம், 10 என்பதனைக் கொண்ட பிஆர் கூகுள் தொடக்கப்பக்கத்திற்கு திருப்பி விடப்படலாம் - பின்னர் அந்தப் புதிய பக்கத்தின் பிஆர் பிஆர்10 என உயர்ந்து விடும். 302 கூகுள் முளை என்றும் அறியப்படும் இந்த ஏமாற்று உத்தி இவ்வாறான முறைமையில் இருந்த ஒரு அறிந்த குறைபாடு அல்லது வழுவாகும். வலைமேலாளரின் விருப்பத்திற்கேற்ப எந்த பக்கத்தின் பேஜ் தரவரிசையையும் உயர்த்தியோ அல்லது தாழ்த்தியோ ஏமாற்றிக் காட்டலாம். மேலும் கூகுளுக்கு மட்டுமே அந்தப் பக்கத்தின் உண்மையான பேஜ் தரவரிசைக்கான அணுக்கம் உள்ளது. பொதுவாக, ஐயப்பாட்டினை உருவாக்கும் பேஜ் தரவரிசை கொண்ட யுஆர்எல்லுக்கு ஒரு கூகுள் தேடலை தொடங்குவதன் மூலம் இந்த ஏமாற்று வேலையை கண்டுபிடிக்கலாம்; ஏனெனில் தனது விளைவுகளில் முற்றிலும் வேறான தளத்தின் (திருப்பி அனுப்பப்பட்ட ஒன்றிற்கு) யுஆர்எல்லை இது காண்பிக்கும்.
பேஜ் தரவரிசையைக் கையாடுதல்[தொகு]
தேடல்-பொறி உகப்புமைத் தேவைகளுக்காக, சில நிறுவனங்கள் வலை மேலாளர்களுக்கு உயர் பேஜ் தரவரிசை இணைப்புகளை விற்க முன் வருகின்றன.[17] உயர்-பிஆர் பக்கங்களின் இணைப்புகள் அதிக மதிப்புடையவை என கருதப்படுவதால் அவை அதிக விலை கொண்டுள்ளன. ஒரு வலை மேலாளரின் இணைப்பின் புகழை உயர்த்துவதற்குத் தரமுள்ள உள்ளடக்க பக்கங்களின் இணைப்பு விளம்பரங்களையும் மற்றும் போக்குவரத்தைச் செலுத்த தொடர்புள்ள தளங்களையும் வாங்குவது ஒரு பயனுள்ள வெற்றிகரமான வியாபார முறையாகும். எனினும், பேஜ் தரவரிசை மற்றும் மதிப்பு வழங்குவதற்காக வலை மேலாளர்கள் இணைப்புகளை விற்பது அல்லது விற்றது கண்டுபிடிக்கப்பட்டால், அவர்களின் இணைப்புகள் மதிப்பிழக்கும் என பொதுவான முறையில் கூகுள் எச்சரிக்கை விடுத்துள்ளது. (மற்ற பக்கங்களின் பேஜ் தரவரிசைகளின் கணிப்பில் ஒதுக்கப்படுகிறது). இணைப்புகளை வாங்கும் மற்றும் விற்கும் நடைமுறை வலை மேலாளர்களிடையே பெரும் வாதத்திற்கு உள்ளாகியிருக்கிறது. ஆதரவளிக்கும் இணைப்புகளில் தொடராத ஹெச்டிஎம்எல் பண்பு மதிப்பை பயன்படுத்துமாறு வலை மேலாளர்களுக்கு கூகுள் ஆலோசனை வழங்குகிறது. மாட் கட்ஸின் கூற்றுப்படி, முறைகளை கையாட முயற்சித்து அதன் மூலம் கூகுள் தேடல் விளைவுகளின் தொடர்பையும் தரத்தையும் குறைக்கும் வலை மேலாளர்களைப் பற்றியே கூகுள் அதிகம் கவலை கொள்கிறது.[17]
நோக்கமுற்ற உலாவர் மாதிரி[தொகு]
மூல பேஜ் தரவரிசை செய்வழி ஒரு முறைமையற்ற உலாவர் மாதிரியைப் பிரதிபலிக்கிறது. அதாவது ஒரு குறிப்பிட்ட பக்கத்தின் பேஜ் தரவரிசை, அங்கொன்றும் இங்கொன்றுமாக இணைப்புகளை அழுத்தும்போது அந்த பக்கத்திற்கு வரும் நிகழ்தகவு கோட்பாட்டிலிருந்து பெறப்படுகிறது. எனினும், உண்மையான பயனர்கள் வலையில் முறைமையற்று உலாவ மாட்டார்கள். ஆனால் தங்களது விருப்பம் மற்றும் குறிக்கோள் ஆகியவற்றிற்கு ஏற்ப இணைப்புகளைத் தொடர்வார்கள். உண்மையான பயனர்கள் ஒரு குறிப்பிட்ட பக்கத்தை எத்தனை முறை பார்வையிடுகிறார்கள் என்பதன் மூலம் அந்தப் பக்கத்தின் முக்கியத்துவத்தை பிரதிபலிக்கும் ஒரு பேஜ் தரவரிசை மாதிரி நோக்கமுற்ற உலாவர் மாதிரி எனக் கூறப்படுகிறது[18]. கூகுள் கருவிப்பலகை காணப்படும் ஒவ்வொரு பக்கத்தைப் பற்றிய தகவலையும் கூகுளுக்கு அனுப்புகிறது; இதன் மூலம் அது, நோக்கமுற்ற உலாவர் மாதிரியை ஆதாரமாகக் கொண்டு பேஜ் தரவரிசையை கணக்கிடுவதற்கு ஒரு அடிப்படையை அளிக்கிறது. மோசடியை எதிர்ப்பதற்கு கூகுள் அறிமுகப்படுத்தியிருக்கும் தொடராத பண்பிற்கு பக்க விளைவுகள் உள்ளன; வலை மேலாளர்கள் தங்கள் பேஜ் தரவரிசையை உயர்த்துவதற்காக வெளி செல்லும் இணைப்பில் இதை வழமையாகப் பயன்படுத்துகின்றனர். இதனால் வலை ஊர்வர்களுக்கு உண்மையான இணைப்புகள் இழப்பை இது விளைவிக்கிறது; இதனால் முறைமையற்ற உலாவர் மாதிரியின் அடிப்படையில் உருவான மூல பேஜ் தரவரிசை செய்வழி நம்பகத்தன்மை அற்றதாகிறது. பயனர்களின் மேலோடி வழக்கங்களைப் பற்றி கூகுள் கருவிப்பலகை வழங்கும் தகவல்களை பயன்படுத்துவது தொடராத பண்பினால் ஏற்படும் தகவல் இழப்பை ஓரளவிற்கு ஈடு செய்கிறது. தேடல் விளைவுகளில் உண்மையிடத்தை நிர்ணயிக்கும் ஒரு பக்கத்தின் ஸெர்ப் தரவரிசை, மற்ற காரணிகளையும் சேர்த்துக் கூடுதலாக முறைமையற்ற உலாவர் மாதிரி மற்றும் நோக்கமுற்ற உலாவர் மாதிரி ஆகியவற்றின் கலவையின் அடிப்படையில் அமையும் [19].
பிற பயன்பாடுகள்[தொகு]
பாரம்பரியமிக்கதான அறிவியல் தகவல்களுக்கான நிறுவனம் (இன்ஸ்டிட்யூட் ஃபார் ஸயிண்டிஃபிக் இன்ஃபர்மேஷன் (ஐஎஸ்ஐ)), விசைப்பயன் காரணிக்கு மாற்றாக பேஜ் தரவரிசையின் ஒரு பதிப்புருவினை முன் மொழிந்து[20] அதனை எய்ஜென்ஃபாக்டர்.ஆர்க் என்பதில் செயல்படுத்தியுள்ளது.
ஒவ்வொரு கட்டுரைக்கும் வரும் மேற்கோள்களை எண்ணுவதை விட, ஒவ்வொரு மேற்கோளின் "முக்கியத்துவமும்" பேஜ் தரவரிசையின் பாணியில் நிர்ணயிக்கப்படுகிறது.
கல்விசார் முனைவர் நிரல்கள், அவை தங்களது பட்டதாரிகளை ஆசிரிய நிலைகளில் வைத்திருக்கும் கோப்புகளின்படி அவற்றை தரவரிசைப்படுத்துவது என்பதானது பேஜ் தர வரிசையின் ஒரு புதிய பயன்பாடு ஆகும். பேஜ் தரவரிசையின் பதங்களில், கல்வி நிலையப் பிரிவுகள் ஒன்றுக்கொன்று தொடர்பு கொண்டு தங்கள் ஆசிரியர்களை ஒன்றிடமிருந்து ஒன்று (தங்களிடமிருந்தும்) ஒப்பந்தப்படுத்துகிறது. [21]
எத்தனை நபர்கள் தனிப்பட்ட இடங்கள் மற்றும் சாலைகளுக்கு வருகிறார்கள் என்பதைக் கண்டறிய இடங்கள் அல்லது சாலைகளை தரவரிசைப்படுத்த பேஜ் தர வரிசை பயன்படுகிறது.[22][23]. சொற்கோவைப் பொருளியலில் வார்த்தை உணர்த்தல் தெளிவு [24] என்பதை செயல்படுத்தவும், மேலும் சொல்வலையின் ஒத்தவார்த்தை தொகுதிகளை அவை எவ்வாறு நேர்மறைத்தன்மை அல்லது எதிர்மறைத்தன்மை போன்ற தமது பொருட்தன்மையை உடையவையாய் இருக்கின்றன என்பதைப் பொறுத்து தாமாகவே தரவரிசைப்படுத்தவும் பயன்படுகிறது. [25]
விக்கிபீடியாவின் கட்டமைப்பை அடிப்படையாகக் கொண்டு வழக்கமான வாசிப்புப் பட்டியலை உருவாக்க பேஜ் தரவரிசையை ஒத்த ஒரு ஆற்றல் வாய்ந்த எடையிடு-முறைமை பயன்படுகிறது. [26]
ஒரு வலை ஊர்வர் பேஜ் தரவரிசையை, மற்ற முக்கியமான மீட்டர் முறைகளில் ஒன்றாக, வலையில் அடுத்து காண நினைக்கும் யுஆர்எல் எது என்பதை நிர்ணயிக்கப் பயன்படுத்தலாம். முன்னர் செயற்பாடு கொண்டிருந்த கட்டுரைகளில் ஒன்றான [27] இது, கூகுளின் உருவாக்கத்தில் பயன்படுத்தப்பட்ட யுஆர்எல் கட்டளையின் வழியாக திறமையாக ஊர்ந்து செல்வது என்பதாகும். [28] இது எத்தனை ஆழமாக, மற்றும் எந்த அளவிற்கு கூகுள் ஒரு தளத்திற்குள் செல்லும் என்பதை நிர்ணயிக்க பல மாறுபட்ட முக்கியமான பதின்ம அடுக்கு முறைகளின் பயன்பாட்டைப் பற்றி விவாதிக்கிறது. ஒரு யுஆர்எல்லுக்கு உள்வரும் மற்றும் வெளிச் செல்லும் பல இணைப்புகள் மற்றும் ஒரு தளத்தின் வேர் அடைவிலிருந்து யுஆர்எல்லுக்கு செல்லும் தூரம் போன்றவை பட்டியலிடப்பட்டாலும், பேஜ் தரவரிசை இத்தகைய பல முக்கியமான மீட்டர் முறைகளுள் ஒன்றாகக் காணப்படுகிறது.
வலை முழுவதிலுமே வலைப்பூ உலகம் (Blogosphere) போன்ற சமூகத்தின் வெளிப்படையான தாக்கத்தை அளப்பதற்கும் பேஜ் தரவரிசையை ஒரு வழி முறை பரணிடப்பட்டது 2010-02-12 at the வந்தவழி இயந்திரம் யாக பயனபடுத்தலாம். அளவீடற்ற வலையமைப்பு உருமாதிரியின் பிரதிபலிப்பில் கவனத்தின் பகிர்மானத்தை அளப்பதற்கு இந்த அணுகுமுறை பேஜ் தரவரிசையைப் பயன்படுத்துகிறது.
எந்த ஒரு சூழலியல் அமைப்பினிலும், சுற்றுச் சூழலின் ஆரோக்கியம் தொடர்வதற்கு அத்தியாவசியமான இனங்களை நிர்ணயிப்பதற்கு பேஜ் தரவரிசையின் ஒரு மேம்பட்ட பதிப்பை பயன்படுத்தலாம்.[29]
கூகுளின் ரெல்[தொகு]
"தொடராத" தேர்வு== 2005ஆம் ஆண்டின் தொடக்கத்தில் தாக்குநிலை தனிமங்களுக்காகவும் ஹெச்டிஎம்எல் இணைப்பின் 'ரெல்' பண்புக்காகவும் கூகுள் "தொடராத [30]" என்னும் புது மதிப்பு ஒன்றை செயல்படுத்தியது; இதனால் வலைதள வடிவமைப்பாளர்கள் மற்றும் வலை உலாவர்கள் பேஜ் தரவரிசைக்காக கூகுள் கருத்தில் எடுக்காத இணைப்புகளை உருவாக்கிக் கொள்ளலாம் - இவை பேஜ் தரவரிசை முறையில் இனி "வாக்கு" இல்லாத இணைப்புகளாகும். இந்த தொடராத உறவு என்பது மோசடியை எதிர்க்கும் ஒரு முயற்சியாக இணைக்கப்பட்டது.
எடுத்துக்காட்டாக, முன்னர் மக்கள் தங்கள் பேஜ் தரவரிசையைச் செயற்கையாக உயர்த்துவதற்காக தங்கள் வலைதளத்திற்கு இணைப்புகளுடன் பல செய்தி-பலகை அஞ்சல்களை உருவாக்க முடிந்தது. தொடராதது என்னும் மதிப்பீடு வந்த பிறகு, செய்தி-பலகை நிர்வாகிகள் அஞ்சல்களின் மீ இணைப்புகள் அனைத்திலும் 'ரெல்=தொடராத' என்பதை தாமாகவே புகுத்துவதற்கு தங்கள் குறிமுறைகளை மேம்படுத்தலாம், இதன் மூலம் அத்தகைய குறிப்பிட்ட அஞ்சல்களினால் பேஜ் தரவரிசை பாதிக்கப்படாமல் தடுக்க முடியும். எனினும், உண்மையான விமரிசனங்களின் இணைப்பு மதிப்பு குறைவது போன்ற பல குறைபாடுகளும் இத்தகைய 'தவிர்ப்பு முறை'யில் உள்ளன. (காண்க: #தொடராத வலைப்பூக்களில் எரிதம்)
ஒரு வலைத் தளத்தின் பக்கங்களுள் பேஜ் தரவரிசை பாய்வதைக் கட்டுப்படுத்தும் மனித முயற்சியாகப் பல வலை மேலாளர்கள் பேஜ் தரவரிசை செதுக்குதல் எனப்படும் நடைமுறையைப் பின்பற்றுகின்றனர்[31] - இது ஒரு வலைமேலாளர் அதிமுக்கியம் எனக் கருதும் பக்கங்களை நோக்கி பேஜ் தர வரிசையை செல்வதைச் சாத்தியமாக்க அந்த வலைத் தளத்தின் குறிப்பிட்ட உள் இணைப்புகளில் 'தொடராத பண்பை' இடும் செயலாகும். 'தொடராத பண்பு' அறிமுகமான காலம் துவங்கியே இந்த உத்தி கையாளப்படுகிறது. ஆயினும், இந்த உத்தி தனது பயனை இழந்து விட்டதாகப் பலரும் கருதுகின்றனர்.[32]
கூகுள் வலை மேலாளரின் கருவிகளிலிருந்து நீக்கம்[தொகு]
2009ஆம் ஆண்டு அக்டோபர் மாதம் 14ஆம் தேதி கூகுள் தனது வலை மேலாளர் கருவிகள் பகுதியிலிருந்து பேஜ் தரவரிசையை நீக்கி விட்டதாக அதன் பணியாளர் சூசன் மோஸ்க்வா (Susan Moskwa) உறுதி செய்தார். "பேஜ் தரவரிசையில் அதிகம் கவனம் செலுத்தக்கூடாது என்று மக்களுக்கு நாங்கள் பல காலமாக கூறி வருகிறோம். பல தள உரிமையாளர்கள் தங்களின் தடத்திற்கு அது அதி முக்கியமான மீட்டர் முறை என எண்ணுகின்றனர்; ஆனால் அது உண்மையல்ல" என அவரது அஞ்சலின் ஒரு பகுதி உரைக்கிறது.[33] மோஸ்க்வாவின் உறுதியளிப்புக்கு பின்னரும் இரண்டு நாட்கள் கூகுள் கருவிப் பலகையின் வலை உபகரணத்தில் பேஜ் தரவரிசை காணப்பட்டது.
குறிப்புகள்[தொகு]
- ↑ "Google Press Center: Fun Facts". www.google.com. Archived from the original on 2009-04-24. பார்க்கப்பட்ட நாள் 2009-10-05.
- ↑ Lisa M. Krieger (1 December 2005). "Stanford Earns $336 Million Off Google Stock". San Jose Mercury News, cited by redOrbit. பார்க்கப்பட்ட நாள் 2009-02-25.
- ↑ Richard Brandt. "Starting Up. How Google got its groove". Stanford magazine. Archived from the original on 2009-03-10. பார்க்கப்பட்ட நாள் 2009-02-25.
- ↑ 4.0 4.1 கூகுள் தொழில்நுட்பம்
- ↑ 5.0 5.1 5.2 5.3 5.4 Sergey Brin, Larry Page(1998). "The Anatomy of a Large-Scale Hypertextual Web Search Engine". Proceedings of the 7th international conference on World Wide Web (WWW), 107–117.
- ↑ David Vise and Mark Malseed (2005). The Google Story. பக். 37. பன்னாட்டுத் தரப்புத்தக எண்:ISBN 0-553-80457-X இம் மூலத்தில் இருந்து 2006-04-28 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20060428055830/http://www.thegooglestory.com/. பார்த்த நாள்: 2010-05-13.
- ↑ ஹெச்டிடிபி://ஸயின்ஸ்.ஸ்லாஷ்டாட்.ஆர்க்/ஸ்டோரி/10/02/17/2317239/பேஜ்ராங்க்-டைப்-அல்காரிதம்-ஃப்ரம்-தி-1940ஸ்-டிஸ்கவர்ட்?ஆர்ட்_போஸ்=3
- ↑ ஹெச்டிடிபி://டபிள்யுடபிள்யுடபிள்யு.டெக்னாலஜிரெவ்யூ.காம்/ப்ளாக்/ஆர்க்ஸிவ்/24821/
- ↑ 9.0 9.1 ஹெச்டிடிபி://ஆர்க்ஸிவ்.ஆர்க்/ஆப்ஸ்/1002.2858
- ↑ மாட் கட்ஸின் வலைப்பூ: கூகுளிலிருந்து நேரடியாக: உங்களுக்கு தெரிய வேண்டியது, அவரது வில்லைகளின் 15ஆம் பக்கத்தில் காண்க.
- ↑ Taher Haveliwala and Sepandar Kamvar. (March 2003). "The Second Eigenvalue of the Google Matrix" (PDF). Stanford University Technical Report. http://www-cs-students.stanford.edu/~taherh/papers/secondeigenvalue.pdf.
- ↑ Gianna M. Del Corso, Antonio Gullí, Francesco Romani (2005). "Fast PageRank Computation via a Sparse Linear System". Internet Mathematics 2 (3). http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.118.5422.
- ↑ Arasu, A. and Novak, J. and Tomkins, A. and Tomlin, J.(2002). "PageRank computation and the structure of the web: Experiments and algorithms". Proceedings of the Eleventh International World Wide Web Conference, Poster Track, 107–117.
- ↑ Aubuchon, Vaughn, "Google Ranking Factors - SEO Checklist", காப்பகப்படுத்தப்பட்ட நகல், archived from the original on 2010-07-19, பார்க்கப்பட்ட நாள் 2010-05-13
- ↑ Fishkin, Rand (April 2, 2007). "Search Engine Ranking Factors - Version 2". seomoz.org. பார்க்கப்பட்ட நாள் May 11, 2009.
{{cite web}}: Unknown parameter|coauthors=ignored (help) - ↑ ஹெச்டிடிபி://ஆர்டிகில்-ப்ளாக்.திஃபாண்டம்ரைட்டர்ஸ்.காம்/கூகுள்-லவ்/2008/08/09/
- ↑ 17.0 17.1 "How to report paid links". mattcutts.com/blog. April 14, 2007. பார்க்கப்பட்ட நாள் 2007-05-28.
- ↑ Jøsang, A. (2007), "Trust and Reputation Systems", in Aldini, A. (ed.), Foundations of Security Analysis and Design IV, FOSAD 2006/2007 Tutorial Lectures. (PDF), Springer LNCS 4677, pp. 209–245, doi:10.1007/978-3-540-74810-6[தொடர்பிழந்த இணைப்பு]
- ↑ SEOnotepad, "Myth of the Google Toolbar Ranking", காப்பகப்படுத்தப்பட்ட நகல், archived from the original on 2010-07-02, பார்க்கப்பட்ட நாள் 2010-05-13
- ↑ Johan Bollen, Marko A. Rodriguez, and Herbert Van de Sompel. (December 2006). "Journal Status". Scientometrics 69 (3). http://www.arxiv.org/abs/cs.GL/0601030.
- ↑ Benjamin M. Schmidt and Matthew M. Chingos (2007). "Ranking Doctoral Programs by Placement: A New Method" (PDF). PS: Political Science and Politics 40 (July): 523–529. http://www.people.fas.harvard.edu/~chingos/rankings_paper.pdf. பார்த்த நாள்: 2010-05-13.
- ↑ B. Jiang (2006). "Ranking spaces for predicting human movement in an urban environment" (PDF). International Journal of Geographical Information Science 23: 823–837. http://arxiv.org/abs/physics/0612011.
- ↑ Jiang B., Zhao S., and Yin J. (2008). "Self-organized natural roads for predicting traffic flow: a sensitivity study" (PDF). Journal of Statistical Mechanics: Theory and Experiment P07008. http://arxiv.org/abs/0804.1630.
- ↑ ராபர்டோ நாவிக்லி, மிரெல்லா லபாடா. மேற்பார்வையிடப்படாத வார்த்தை உணர்த்தல் தெளிவிற்கு வரைபட தொடர்பின் ஒரு சோதனைப் படிப்பு. மாதிரி பகுப்பாய்வு மற்றும் இயந்திர அறிவுத் திறம் ஆகியவற்றில் ஐஈஈஈ பரிமாற்றங்கள் (டிபிஏஎம்ஐ), 32(4), ஐஈஈஈ ப்ரெஸ், 2010, பிபி. 678-692.
- ↑ Andrea Esuli and Fabrizio Sebastiani. "PageRanking WordNet synsets: An Application to Opinion-Related Properties" (PDF). In Proceedings of the 35th Meeting of the Association for Computational Linguistics, Prague, CZ, 2007, pp. 424-431. பார்க்கப்பட்ட நாள் June 30, 2007.
{{cite web}}: Unknown parameter|dateformat=ignored (help) - ↑ Wissner-Gross, A. D. (2006). "Preparation of topical readings lists from the link structure of Wikipedia". Proceedings of the IEEE International Conference on Advanced Learning Technology (Rolduc, Netherlands): 825. doi:10.1109/ICALT.2006.1652568.
- ↑ "Working Papers Concerning the Creation of Google". Google. பார்க்கப்பட்ட நாள் November 29, 2006.
{{cite web}}: Unknown parameter|dateformat=ignored (help) - ↑ Cho, J., Garcia-Molina, H., and Page, L. (1998). "Efficient crawling through URL ordering". Proceedings of the seventh conference on World Wide Web (Brisbane, Australia).
- ↑ கூகுள் வித்தை வழக்கொழிதல்களைத் தடமறிகிறது
- ↑ "Preventing Comment Spam". Google. பார்க்கப்பட்ட நாள் January 1, 2005.
{{cite web}}: Unknown parameter|dateformat=ignored (help) - ↑ ஹெச்டிடிபி://டபிள்யுடபிள்யுடபிள்யு.சியோமோஜ்.ஆர்க்/ப்ளாக்/பேஜ்ராங்க்-ஸ்கல்ப்டிங்க்-பார்ஸிங்க்-தி-வேல்யு-அண்ட்-பொடென்ஷியல்-பெனிஃபிட்ஸ்-ஆஃப்-ஸ்கல்ப்டிங்க்-பிஆர்-வித்-நோஃபாலோ
- ↑ ஹெச்டிடிபி://டபிள்யுடபிள்யுடபிள்யு.மாட்கட்ஸ்.காம்/ப்ளாக்/பேஜ்ராங்க்-ஸ்கல்ப்டிங்க்/
- ↑ Susan Moskwa, "PageRank Distribution Removed From WMT", http://www.google.com/support/forum/p/Webmasters/thread?tid=6a1d6250e26e9e48&hl=en, பார்க்கப்பட்ட நாள் October 16, 2009
{{citation}}: Missing or empty|title=(help); Unknown parameter|dateformat=ignored (help)
புற இணைப்புகள்[தொகு]
- கூகுளின் எங்கள் தேடல்: கூகுள் தொழில்நுட்பம்
- அமெரிக்கக் கணித சமுதாயத்தின் எவ்வாறு வலையின் வைக்கோற் போரில் உங்களது ஊசியை கூகுள் கண்டுபிடிக்கிறது
- யூ எஸ் உரிமம் பெற்ற மூல பேஜ் தரவரிசை - இணைக்கப்பட்ட தரவுத் தளத்தில் கணு தரவரிசைக்கான முறை பரணிடப்பட்டது 2014-08-29 at the வந்தவழி இயந்திரம் - செப்டம்பர் 4, 2001
- யூ எஸ் உரிமம் பெற்ற மூல பேஜ் தரவரிசை - இணைக்கப்பட்ட தரவுத் தளத்தில் ஆவணங்களின் மதிப்பீட்டு முறை பரணிடப்பட்டது 2021-02-24 at the வந்தவழி இயந்திரம் - செப்டம்பர் 28, 2004
- யூ எஸ் உரிமம் பெற்ற மூல பேஜ் தரவரிசை - இணைக்கப்பட்ட தரவுத் தளத்தில் கணு தரவரிசைக்கான முறை பரணிடப்பட்டது 2019-08-28 at the வந்தவழி இயந்திரம் - ஜூன் 6, 2006
- யூ எஸ் உரிமம் பெற்ற மூல பேஜ் தரவரிசை - இணைக்கப்பட்ட தரவுத் தளத்தில் ஆவணங்களின் மதிப்பீடு பரணிடப்பட்டது 2018-03-31 at the வந்தவழி இயந்திரம் - செப்டம்பர் 11, 2007
- 1940ஆம் ஆண்டுகளிலேயே, பேஜ் தரவரிசை வகை செய்வழியை விஞ்ஞானி கண்டுபிடித்துள்ளார் பரணிடப்பட்டது 2010-05-29 at the வந்தவழி இயந்திரம் - பிப்ரவரி 17,2010






















































