இயல்நிலைப் பரவல்

Probability density function சிவப்பு நிற வளைகோடு திட்ட இயல்நிலைப் பரவலுக்குரியது.
Cumulative distribution function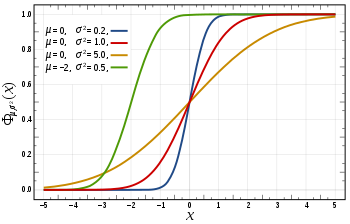
குறியீடு  :	${\mathcal {N}}(\mu ,\,\sigma ^{2})$
பண்பளவைகள்:	μ ∈ R — சராசரி σ2 > 0 — பரவற்படி
தாங்கி:	x ∈ R
pdf:	${\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\,e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$
cdf:	${\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sqrt {2\sigma ^{2}}}}\right)\right]$
சராசரி:	μ
இடைநிலையளவு:	μ
முகடு:	μ
variance:	σ2
கோணல்:	0
தட்டையளவு:	0
சிதறம்(என்ட்ரோப்பி):	${\frac {1}{2}}\ln(2\pi e\,\sigma ^{2})$
mgf:	$\exp\{\mu t+{\frac {1}{2}}\sigma ^{2}t^{2}\}$
cf:	$\exp\{i\mu t-{\frac {1}{2}}\sigma ^{2}t^{2}\}$
ஃபிஷர் தகவல்:	${\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}$

புள்ளியியலின், நிகழ்தகவுக் கோட்பாட்டில், இயல்நிலைப் பரவல் அல்லது இயற் பரவல் (normal distribution) என்பது ஒரு தொடர் நிகழ்தகவுப் பரவலாகும். ஒரு சமவாய்ப்பு மாறியின் மெய்மதிப்புகள், சராசரி மதிப்பைச் சுற்றி நெருக்கமாக அணுகும் தோராயநிலையை விளக்குவதற்கு இப்பரவல் பெரும்பாலும் பயன்படுகிறது.

இப்பரவலின் நிகழ்தகவு அடர்த்திச் சார்பு:

$f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}},$

பண்பளவைகள்(parameters) μ -பரவலின் சராசரியையும், σ² -பரவற்படியையும் குறிக்கும்.

இச்சார்பின் வளைவரை மணிவடிவில் அமையும். இவ்வளைவரை காசியன் வளைவரை அல்லது மணி வளைவரை என அழைக்கப்படுகிறது. μ = 0 மற்றும் σ² = 1 கொண்ட பரவல், திட்ட இயல்நிலைப் பரவல் அல்லது செந்தர இயல்நிலைப் பரவல் (standardized normal distribution) எனப்படும்.

புள்ளியியலில் இயல்நிலைப் பரவல் முக்கியமான ஒன்றாகக் கருதப்படுவதற்குப் பல காரணங்கள் உள்ளன. இயல்நிலைப் பரவலைச் சேர்ந்த பெரும்பாலான முடிவுகளைத் தெளிவாகக் காண முடியுமென்பதால் இப்பரவலைப் பகுப்பாய்வு முறையில் விளக்க முடியுமென்பது முதல் காரணமாகும். சில எளிய நிபந்தனைகளின் கீழ், அதிக அளவிலான சமவாய்ப்பு மாறிகளின் கூடுதலானது இயல்நிலைப் பரவலைப் பின்பற்றுகிறது என்ற கூற்றை எடுத்துரைக்கும் மைய எல்லைத் தேற்றத்தின் பின்விளைவாக இயல்நிலைப் பரவல் உருவானது. இரண்டாவது காரணம், நடைமுறை நிகழ்வுகளில் நாம் காணும் பலவகையான சமவாய்ப்பு மாறிகளை மாதிரிப்படுத்துவதற்கு இயல்நிலைப் பரவலின் மணிவடிவம் வசதியாக இருப்பது ஆகும். இயல்நிலைப் பரவலானது புள்ளியியல், தாவரவியல் மற்றும் சமூக அறிவியலில் சிக்கலான தோற்றப்பாடுகளுக்கான (phenomena) எளிய மாதிரியாகப் பயன்படுத்தப்படுகிறது.

வரையறை

இயல்நிலைப் பரவலின் எளியவகை, திட்ட இயல்நிலைப் பரவலாகும்.

திட்ட இயல்நிலைப் பரவலின் நிகழ்தவு அடர்த்திச் சார்பு:

$\phi (x)={\frac {1}{\sqrt {2\pi }}}\,e^{-{\frac {\scriptscriptstyle 1}{\scriptscriptstyle 2}}x^{2}}.$

இச்சார்பைப் பின்வரும் வகைக்கெழுச் சமன்பாடுகளைச் சரிசெய்யும் சார்பு f(x) ஆகவும் வரையறுக்கலாம்:

$\int _{-\infty }^{\infty }\!f(x)dx=1$

$\int _{-\infty }^{\infty }\!xf(x)dx=\mu$

$\int _{-\infty }^{\infty }\!(f(x)-\mu )^{2}=\sigma ^{2}$

இச்சமன்பாடுகளைத் தீர்ப்பதன் மூலம் கிடைக்கும் இயல்நிலைப் பரவலின் சார்பு வடிவம்: $f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\,e^{\frac {-(x-\mu )^{2}}{2\sigma ^{2}}}$

இதிலுள்ள $\scriptstyle \ 1/{\sqrt {2\pi }}$ காரணி, இச்சார்பின் வளைவரையின் பரப்பு ஒரு அலகு என்பதை உறுதிப்படுத்துகிறது. அடுக்கிலுள்ள 1/2, வளைவரையின் அகலத்தை (வளைவுமாற்றுப் புள்ளிகளுக்கிடையே உள்ள தூரத்தில் பாதியளவு) ஒரு அலகாக்குகிறது. புள்ளியியலில் ஏனைய நிகழ்தகவுப்பரவல்களின் அடர்த்திச் சார்புகள் f அல்லது p எனக் குறிக்கப்படுகிறது. ஆயினும் இப்பரவலின் அடர்த்திச் சார்பை ϕ (phi) என்ற கிரேக்க எழுத்தால் குறிப்பது வழக்கமாக உள்ளது. பொதுவாக,ஒரு இருபடிச் சார்பை அடுக்கேற்றப்படுத்துவதன் மூலம் இயல்நிலைப் பரவலைக் காணலாம்:

$f(x)=e^{ax^{2}+bx+c}.\,$

இச்சார்பின் வளைவரை மணிவடிவமாக இருக்கும். இச்சார்பு குழிவானதாக இருப்பதற்கு, a < 0 ஆக இருக்க வேண்டும். எப்பொழுதும் f(x) > 0 ஆக உள்ளது. a ன் மதிப்பை மாற்றுவதன் மூலம் மணி வளைவரையின் அகலத்தைக் கட்டுப்படுத்தலாம். b ன் மதிப்பை மாற்றுவதன் மூலம் மணியின் நடுமுகடினை x அச்சின் திசையில் நகர்த்தலாம். c ன் மதிப்பை மாற்றுவதன் மூலம் முகடின் உயரத்தைக் கட்டுப்படுத்தலாம். f(x) ஆனது உண்மையிலேயே Rன் மீதான ஒரு நிகழ்தகவு அடர்த்திச் சார்பாக இருப்பதற்கு, $\scriptstyle \int _{-\infty }^{\infty }f(x)\,dx\ =\ 1$ என்றிருக்குமாறு c ன் மதிப்பைத் தேர்ந்தெடுக்க வேண்டும் (இதற்கு  a < 0 என இருப்பதும் அவசியம்).

a, b, and c குப் பதில், சராசரி μ = -b/2a மற்றும் பரவற்படி σ² = 1/2a என்பதைப் பயன்படுத்தலாம். இப்புதிய பண்பளவைகளைப் பயன்படுத்தி நிகழ்தகவு அடர்த்திச்சார்பினை வசதியானதொரு திட்ட வடிவில் மாற்றிக் கொள்ளலாம்:

$f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\,e^{\frac {-(x-\mu )^{2}}{2\sigma ^{2}}}={\frac {1}{\sigma }}\,\phi \!\left({\frac {x-\mu }{\sigma }}\right).$

திட்ட இயல்நிலைப் பரவலின் சராசரி μ = 0 மற்றும் பரவற்படி σ² = 1 ஆகவும் அமைவதைக் காண்க. திட்ட இயல்நிலைப் பரவலை  σ அளவு கிடைமட்டமாக நீட்டிப்பதாலும்  μ அளவு வலப்புறத்தில் பெயர்ச்சி செய்வதாலும் கிடைக்கக்கூடிய பரவலாக எந்தவொரு இயல்நிலைப் பரவலையும் கருதலாம் என்பதை மேலே தரப்பட்ட சமன்பாட்டின் இறுதிப் பகுதியானது காட்டுகிறது.

பண்பளவைகள் μ மற்றும் σ இரண்டும் முறையே மணி வளைவரையின் நடுமுகட்டையும் அகலத்தையும் குறிக்கும். அதேசமயம் இயல்நிலைப் பரவலின் சராசரி, இடைநிலை மற்றும் முகடு மூன்றும் சமமாக இருக்கும். அவை மூன்றையும் μ குறிக்கிறது. சமவாய்ப்பு மாறியின் மதிப்புகள், சராசரியைச் சுற்றி எவ்வாறு பரவியுள்ளது என்பதை σ² தருகிறது. இது பரவற்படி என அழைக்கப்படுகிறது. σ² ன் வர்க்க மூலம் பரவலின் திட்ட விலக்கமாகும்.

இயல்நிலைப் பரவலின் குறியீடு: N(μ, σ²).

சராசரி μ மற்றும் பரவற்படி σ² கொண்ட இயல்நிலை சமவாய்ப்பு மாறியின் குறியீடு: $X\ \sim \ {\mathcal {N}}(\mu ,\,\sigma ^{2}).\,$

நிகழ்தகவு அடர்த்திச் சார்பு

இயல்நிலைப் பரவலின் நிகழ்தவு அடர்த்திச் சார்பு (probability density function-pdf):

$f(x;\,\mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\,e^{-(x-\mu )^{2}\!/(2\sigma ^{2})}={\frac {1}{\sigma }}\,\phi \!\left({\frac {x-\mu }{\sigma }}\right),\qquad x\in \mathbb {R} .$

பரவற்படி, σ² பூச்சியமாக இல்லாமல் இருந்தால் மட்டுமே இச்சார்பு முறைமைச் சார்பாக (proper function) இருக்கும். அப்பொழுது இச்சார்பு, முழு மெய்யெண் கோட்டின்மீது வரையறுக்கப்பட்ட ஒரு தொடர்ச்சியான சார்பாக அமையும். மேலும் இச்சார்பு காசியன் சார்பு எனவும் அழைக்கபடுகிறது.

பண்புகள்:

• சார்பு f(x) ஒரேயொரு முகட்டினை உடையது. முகடு x = μ -ஐப்பொறுத்து சமச்சீரானது. இயல்நிலைப் பரவலுக்குச் சராசரி, இடைநிலையளவு, முகடு மூன்றும் சமமாக இருக்கும்.
• இச்சார்பின் வளைவு மாற்றப் புள்ளிகள் சராசரியிலிருந்து இருபுறமும் σ அளவு தூரத்தில் அமைகின்றன. அதாவது, வளைவு மாற்றப் புள்ளிகள், x = μ − σ மற்றும் x = μ + σ புள்ளிகளில் அமைகின்றன.
• சார்பு f(x) மடக்கை-குழிவாகும்.(Logarithmically concave function)
• திட்ட இயல்நிலைப் பரவலின் அடர்த்திச் சார்பு ϕ(x), வூரியே மாற்றின் ஐசன் சார்பாகும்.
• f(x) முடிவில்லாமல் வகையிடத்தக்கது.
• ϕ(x)ன் முதல் வகைக்கெழு; ϕ′(x) = −x·ϕ(x);
  • இரண்டாம் வகைக்கெழு; ϕ′′(x) = (x² − 1)ϕ(x).
  • பொதுவாக n-ஆம் வகைக்கெழு; ϕ⁽ⁿ⁾(x) = (−1)ⁿH_n(x)ϕ(x),
  • H_n என்பது n ஆம் வரிசை ஹெர்மைட் பல்லுறுப்புக் கோவையாகும்.

சேர்ப்பு அடர்த்திச் சார்பு.

சேர்ப்பு அடர்த்திச் சார்பானது (Cumulative distribution function-cdf), (−∞, x] இடைவெளியிலுள்ள மதிப்புகளை எடுக்கும் சமவாய்ப்பு மாறியின் நிகழ்தகவுகளைப் பற்றி விளக்குகிறது. திட்ட இயல்நிலைப் பரவலின் cdf -ன் குறியீடு, Φ ஆகும்.(phi -கிரேக்க முகப்பெழுத்து) அதனை நிகழ்தகவு அடர்த்திச்சார்பின் தொகையீடாகப் பின்வரும் சூத்திரத்தைப் பயன்படுத்திக் கணக்கிடலாம்:

$\Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt={\frac {1}{2}}\left[\,1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\,\right],\quad x\in \mathbb {R} .$

இத்தொகையீட்டை erf, எனச் சுருக்கமாகக் குறிக்கப்படும் சிறப்புச் சார்பான பிழைச் சார்பு(error function)மூலம் எழுதலாம். சராசரி μ மற்றும் பரவற்படி σ² > 0 கொண்ட இயல்நிலை சமவாய்ப்பு மாறியின் cdf :

$F(x;\,\mu ,\sigma ^{2})=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[\,1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\,\right],\quad x\in \mathbb {R} .$

திட்ட இயல்நிலைப் பரவலின் cdf -ன் நிரப்பி: Q(x) = 1 − Φ(x), இது Q-சார்பு என பொறியியலில் அழைக்கப்படுகிறது.

பண்புகள்:

• திட்ட இயல்நிலைப் பரவலின் cdf, (0, ½) இடைவெளியிலுள்ள புள்ளியைப் பொறுத்து இருமடிப்பு சுழற்சி சமச்சீருடையது;

Φ(−x) = 1 − Φ(x).

• Φ(x) -ன் வகையீடு, திட்ட இயல்நிலை அடர்த்திச் சார்பு (pdf), ϕ(x) க்குச் சமம்:

  Φ′(x) = ϕ(x).

• Φ(x) ன் எதிர்வகையீடு:

  ∫ Φ(x) dx = x Φ(x) + ϕ(x).

பரவற்படி பூச்சியமாகக் கொண்ட இயல்நிலைப் பரவலின் cdf, ஹெவிசைட் படிச் சார்பாகும்.(Heaviside step function) (H(0) = 1 என்று எடுத்துக் கொள்வது மரபு.)

$F(x;\,\mu ,0)=\mathbf {1} \{x\geq \mu \}\,.$

மதிப்பளவை சார்பு

திட்ட இயல்நிலை cdf ன் நேர்மாறானது, மதிப்பளவை சார்பு (Quantile function) என அழைக்கப்படுகிறது. மேலும் அச்சார்பு பிழைச் சார்பின் நேர்மாறுச் சார்பின் மூலம் தரப்படுகிறது:

$\Phi ^{-1}(p)\equiv z_{p}={\sqrt {2}}\;\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$

திட்ட இயல்நிலைப் பரவலின் மதிப்பளவைகள், பொதுவாக z_p என க் குறியிடப்படுகின்றன. மதிப்பளவை z_p என்பது, ஒரு திட்ட இயல்நிலை சமவாய்ப்பு மாறியானது அதன் மதிப்புகள் (−∞, z_p] இடைவெளியில் அமைவதற்கான நிகழ்தகவு சரியாக p என இருப்பதற்காக அம்மாறி எடுக்கக்கூடிய மதிப்பினைக் குறிக்கிறது. எடுகோள் சோதனை, நம்ப இடைவெளிவெளிகள் அமைத்தல் மற்றும் Q-Q பிளாட்டுகளில் மதிப்பளவைகள் பயன்படுகின்றன.

மிக முக்கியமான இயல்நிலை மதிப்பளவை: 1.96 = z_0.975. ஒரு திட்ட இயல்நிலை சமவாய்ப்பு மாறியின் தனிமதிப்பு 1.96 க்கும் அதிகமாக 5% நிகழ்வுகளில் இருக்கும்.

சராசரி μ மற்றும் பரவற்படி σ², கொண்ட இயல்நிலை சமவாய்ப்பு மாறியின் மதிப்பளவை சார்பு:

$F^{-1}(p;\,\mu ,\sigma ^{2})=\mu +\sigma \Phi ^{-1}(p)=\mu +\sigma {\sqrt {2}}\,\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$

சிறப்பியல்புச் சார்பு மற்றும் விலக்களவுகள் பிறப்பிக்கும் சார்பு

X என்ற சமவாய்ப்பு மாறியின் சிறப்பியல்பு சார்பு (Characteristic function): φ_X(t) என்பது e^itX -ன் எதிர்பார்ப்பு மதிப்பாகும். இதில், i கற்பனை அலகு; t ∈ R , சிறப்பியல்புச் சார்பின் கோணவீச்சாகும் (argument). சிறப்பியல்புச் சார்பானது, நிகழ்தகவு அடர்த்திச் சார்பு ϕ(x) -ன் வூரியே மாற்றாக அமையும்.

சராசரி μ மற்றும் பரவற்படி σ², கொண்ட இயல்நிலைச் சமவாய்ப்பு மாறி X -ன் சிறப்பியல்புச் சார்பு:

$\varphi (t;\,\mu ,\sigma ^{2})=\int _{-\infty }^{\infty }\!e^{itx}{\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {1}{2}}(x-\mu )^{2}/\sigma ^{2}}dx=e^{i\mu t-{\frac {1}{2}}\sigma ^{2}t^{2}}.$

சிறப்பியல்புச் சார்பை சிக்கலெண் தளம் முழுவதிலும் விரிவாக்கம் செய்யலாம்:

φ(z) = e^{iμz − 1/2σ2z2} for all z ∈ 'C'.

விலக்களவுகள் பிறப்பிக்கும் சார்பானது (moment generating function) e^tX -ன் எதிர்பார்ப்பு மதிப்பாக வரையறுக்கப்படுகிறது.

ஒரு இயல்நிலைச் சமவாய்ப்பு மாறியின் விலக்களவுகள் பிறப்பிக்கும் சார்பு:

$M(t;\,\mu ,\sigma ^{2})=\operatorname {E} [e^{tX}]=\varphi (-it;\,\mu ,\sigma ^{2})=e^{\mu t+{\frac {1}{2}}\sigma ^{2}t^{2}}.$

குவிப்பெருக்கம் பிறப்பிக்கும் சார்பானது விலக்களவுகள் பிறப்பிக்கும் சார்பின் மடக்கையாகும்:

$g(t;\,\mu ,\sigma ^{2})=\ln M(t;\,\mu ,\sigma ^{2})=\mu t+{\frac {1}{2}}\sigma ^{2}t^{2}.$

இது t-ல் அமைந்த ஒரு இருபடிக் கோவையானதால் முதல் இரு குவிப்பெருக்கங்கள்(cumulants) மட்டுமே பூச்சியமற்றதாகும்.

விலக்களவுகள்

இயல்நிலைப் பரவலுக்கு அனைத்து வரிசை விலக்களவுகளும் (Moments) உண்டு. சராசரி μ மற்றும் பரவற்படி σ² கொண்ட இயல்நிலை சமவாய்ப்பு மாறி X -ன் எதிர்பார்ப்பு E|X|^p காண இயலும். மேலும் அது Re[p] > −1என்றவாறுள்ள அனைத்து p -ன் மதிப்புகளுக்கும் முடிவுறு மதிப்பாக இருக்கும். பொதுவாக, p = 1, 2, 3, … என்ற முழு எண் வரிசையிலான விலக்களவுகள்தான் கருத்திற் கொள்ளப்படுகின்றன.

• மைய விலக்களவுகள்(Central moments) என்பவை சராசரி μ-ஐப் பொறுத்த X ன் விலக்களவுகள் ஆகும். எனவே p வரிசையுடைய மைய விலக்களவு என்பது (X − μ)^pன் எதிர்பார்ப்பு மதிப்பாகும்.

  $\mathrm {E} \left[(X-\mu )^{p}\right]={\begin{cases}0&{\text{if }}p{\text{ is odd,}}\\\sigma ^{p}\,(p-1)!!&{\text{if }}p{\text{ is even.}}\end{cases}}$

  இங்கு n!! என்பது இரட்டைக் தொடர் பெருக்கம், அதாவது n முதல் 1 வரையிலான அனைத்து ஒற்றையெண்களின் பெருக்குத்தொகையைக் குறிக்கும்.
  • திட்ட இயல்நிலை சமவாய்ப்பு மாறி(Z) -ன் எதிர்பார்ப்பு மதிப்பு:

  σ^p · E[Z^p]

• மைய தனிமதிப்பு விலக்களவுகள்(Central absolute moments ) என்பவை |X − μ| -ன் விலக்களவுகள் ஆகும். இவை இரட்டை வரிசைகளுக்கு, வழக்கமான விலக்களவுகளாகவும் ஒற்றை வரிசைகளுக்குப் பூச்சியமற்றவையாகவும் இருக்கும்.

  $\operatorname {E} \left[|X-\mu |^{p}\right]=\sigma ^{p}(p-1)!!\cdot \left.{\begin{cases}{\sqrt {2/\pi }}&{\text{if }}p{\text{ is odd}},\\1&{\text{if }}p{\text{ is even}},\end{cases}}\right\}=\sigma ^{p}\cdot {\frac {2^{\frac {p}{2}}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}$

  முழுஎண் அல்லாத p > −1 -க்கு கடைசி சூத்திரம் மெய்யாகும்.
• மூல விலக்களவுகள் மற்றும் மூல தனிமதிப்பு விலக்களவுகள்(Raw moments and raw absolute moments) என்பவை முறையே X மற்றும் |X| -ன் விலக்களவுகள் ஆகும்.

  ${\begin{aligned}&\operatorname {E} \left[X^{p}\right]=\sigma ^{p}\cdot (-i{\sqrt {2}}\operatorname {sgn} \mu )^{p}\;U\left({-{\frac {1}{2}}p},\,{\frac {1}{2}},\,-{\frac {1}{2}}(\mu /\sigma )^{2}\right),\\&\operatorname {E} \left[|X|^{p}\right]=\sigma ^{p}\cdot 2^{\frac {p}{2}}{\frac {\Gamma \left({\frac {1+p}{2}}\right)}{\sqrt {\pi }}}\;_{1}F_{1}\left({-{\frac {1}{2}}p},\,{\frac {1}{2}},\,-{\frac {1}{2}}(\mu /\sigma )^{2}\right).\\\end{aligned}}$

  p -ன் மதிப்பு முழு எண்ணாக இல்லையென்றாலும் இவை பொருந்தும்.
• முதல் இரு குவிப்பெருக்கங்கள், μ மற்றும் σ² ஆகும். ஏனைய உயர்வரிசை குவிப்பெருக்கங்கள் அனைத்தும் பூச்சியமாகும்.

வரிசை	மூல விலக்களவு	மைய விலக்களவு	குவிப் பெருக்கம்
1	μ	0	μ
2	μ2 + σ2	σ 2	σ 2
3	μ3 + 3μσ2	0	0
4	μ4 + 6μ2σ2 + 3σ4	3σ 4	0
5	μ5 + 10μ3σ2 + 15μσ4	0	0
6	μ6 + 15μ4σ2 + 45μ2σ4 + 15σ6	15σ 6	0
7	μ7 + 21μ5σ2 + 105μ3σ4 + 105μσ6	0	0
8	μ8 + 28μ6σ2 + 210μ4σ4 + 420μ2σ6 + 105σ8	105σ 8	0

இயல்நிலை சமவாய்ப்பு மாறியைத் திட்டப்படுத்துதல்

அனைத்து இயல்நிலை சமவாய்ப்பு மாறிகளையும் திட்ட இயல்நிலை சமவாய்ப்பு மாறிகளுடன் தொடர்புபடுத்தலாம். சராசரி μ மற்றும் பரவற்படி σ² கொண்ட இயல்நிலை சமவாய்ப்பு மாறி X எனில்,

$Z={\frac {X-\mu }{\sigma }}$

என்பது சராசரி 0 மற்றும் பரவற்படி 1 கொண்ட திட்ட இயல்நிலை சமவாய்ப்பு மாறியாகும். மறுதலையாக Z எனும் திட்ட இயல்நிலை சமவாய்ப்பு மாறியைக் கொண்டு, சராசரி μ மற்றும் பரவற்படி σ² கொண்ட இயல்நிலை சமவாய்ப்பு மாறி X -ஐக் காணமுடியும்:

$X=\sigma Z+\mu .\,$

திட்ட இயல்நிலைப் பரவலின் pdf மற்றும் cdf -ன் மதிப்புகள் அட்டவணையைப் பயன்படுத்தி அதன் இயல்நிலைப் பரவலின் pdf மற்றும் cdf -ன் மதிப்புகளைக் கணக்கிடுவது எளிதாக இருப்பதால், ஒரு இயல்நிலை சமவாய்ப்பு மாறியைத் திட்டப்படுத்துவது (Standardizing normal random variable) பயனுள்ளதாகவும் வசதியானதுமாக அமைகிறது. ஒரு இயல்நிலைப்பரவல் மற்றும் அதன் திட்ட இயல்நிலைப் பரவலின் pdf மற்றும் cdf இரண்டிற்கும் உள்ள தொடர்பு:

$F_{X}(x)=\Phi \left({\frac {x-\mu }{\sigma }}\right),\quad f_{X}(x)={\frac {1}{\sigma }}\,\phi \left({\frac {x-\mu }{\sigma }}\right).$

திட்ட விலக்கம் மற்றும் நம்பக இடைவெளிகள்

கருநீலநிறப் பரப்பு சராசரியிலிருந்து 1σ (68%), கரு மற்றும் நடுத்தர நீலநிறப் பரப்பு சராசரியிலிருந்து 2σ (95%), லேசான, நடுத்தர மற்றும் கருநீலநிறப் பரப்பு சராசரியிலிருந்து 3σ (99.7%) தூரத்துக்குள் அமையும் இயல்நிலைப் பரவலைக் குறிக்கிறது.

ஒரு இயல்நிலைப் பரவலில் கிட்டத்தட்ட 68% மதிப்புகள் சராசரியிலிருந்து σ அளவு தூரத்துக்குள் அமையும்; 95% மதிப்புகள் சராசரியிலிருந்து 2σ தூரத்துக்குள் அமையும்; 99.7% மதிப்புகள் சராசரியிலிருந்து 3σ தூரத்துக்குள்ளும் அமையும். இக்கருத்து 68-95-99.7 விதி, அல்லதுஅனுபவ விதி அல்லது 3- சிக்மா விதி என அழைக்கப்படுகிறது. இன்னும் துல்லியமாகச் சொல்லவேண்டுமெனில், மணி வளைவரையில் μ − nσ மற்றும் μ + nσ-க்கிடையேயுள்ள பரப்பு:

$F(\mu +n\sigma ;\,\mu ,\sigma ^{2})-F(\mu -n\sigma ;\,\mu ,\sigma ^{2})=\Phi (n)-\Phi (-n)=\mathrm {erf} \left({\frac {n}{\sqrt {2}}}\right),$

இங்கு erf என்பது பிழைச் சார்பாகும்.