இணைகரத்திண்மம்

இணைகரத்திண்மம்
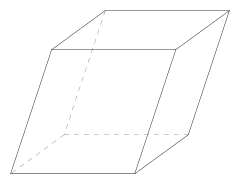
வகை	பட்டகம்
முகங்கள்	6 இணைகரங்கள்
விளிம்புகள்	12
உச்சிகள்	8
சமச்சீர் குலம்	Ci, [2+,2+], (1×)
பண்புகள்	குவிவு

வடிவவியலில் இணைகரத்திண்மம் (parallelepiped) என்பது ஆறு இணைகரங்களால் அடைவுபெற்ற குவிவு முப்பரிமாண திண்ம வடிவம். (சில சமயங்களில் ராம்பாய்ட் (rhomboid) என்ற சொல் இதே பொருளில் பயன்படுத்தப்படுகிறது.)

இணைகரத்திண்மத்தின் மூன்று சமான வரையறைகள்:

• ஒவ்வொரு முகங்களையும் இணைகரமாகக் கொண்ட ஒரு அறுமுகத்திண்மம்.
• மூன்று சோடி இணைபக்கங்கள் கொண்ட அறுமுகத்திண்மம்.
• இணைகர அடிப்பாகமுடைய ஒரு பட்டகம்.

கனசெவ்வகம், கனசதுரம் மற்றும் சாய்சதுரத்திண்மம் ஆகிய மூன்றும் இணைகரத்திண்மங்களின் சிறப்பு வகைகள்.

பண்புகள்

ஒரு இணைகரத்தின்மத்தின் மூன்று சோடி இணையான முகங்களில் எந்தவொன்றையும் அடிப்பாகமாகக் கொள்ளலாம்.

நான்கு இணையான பக்கங்கள் கொண்ட மூன்று தொகுதிகள் உள்ளன. ஒவ்வொரு தொகுதியிலும் உள்ள நான்கு பக்கங்களும் சம நீளமுள்ளவையாக இருக்கும்.

கனசதுரத்தின் நேரியல் உருமாற்றமாக இணைகரத்திண்மம் அமைகிறது.

கனஅளவு

மூன்று திசையன்களால் அமையும் இணைகரத்திண்மம்.

ஒரு இணைகரத்திண்மத்தின் கனஅளவு, அதன் அடிப்பக்க முகத்தின் பரப்பு A மற்றும் அதன் உயரம் h -ன் பெருக்குத்தொகை. இணைகரத்திண்மத்தின் ஆறுமுகங்களில் எந்தவொன்றையும் அடிப்பாகமாக எடுத்துக் கொள்ளலாம். அடிப்பக்க முகத்திற்கும் அதன் எதிர்முகத்திற்கும் இடையே உள்ள செங்குத்து தூரம் இணைகரத்திண்மத்தின் உயரம்.

மாற்று முறை:

வெக்டர்கள் a = (a₁, a₂, a₃), b = (b₁, b₂, b₃) மற்றும் c = (c₁, c₂, c₃) ஆகிய மூன்றும் ஒரு இணைகரத்திண்மத்தின் ஒரு முனை விளிம்புகளாக அமைந்தால் அந்த இணைகரத்திண்மத்தின் கனஅளவு, இம்மூன்று வெக்டர்களின் திசையிலி முப்பெருக்கம் a · (b × c) -ன் தனிமதிப்பாகும்:

$V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|=|\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )|=|\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} )|$

b மற்றும் c -இரண்டையும் இணைகரத்திண்மத்தின் அடிப்பக்க இணைகரத்தின் அடுத்துள்ள விளிம்புகளாகக் கொண்டால், குறுக்குப் பெருக்கத்தின் வடிவவியல் விளக்கத்தின்படி:

A = |b| |c| sin θ = |b × c|,

இங்கு θ , b மற்றும் c -இவற்றுக்கு இடையே உள்ள கோணம்.

இணைகரத்திண்மத்தின் உயரம்:

h = |a| cos α,

இங்கு α , a மற்றும் h -இவற்றுக்கு இடையே உள்ள உட்கோணம்.

படத்திலிருந்து கோணம் α -ன் மதிப்பு: 0° ≤ α < 90°.

மாறாக வெக்டர் b × c , a வெக்டருடன் உருவாக்கும் கோணம் β , 90°-ஐ விட அதிகமாகவும் இருக்கலாம்:

(0° ≤ β ≤ 180°).

b × c , h -க்கு இணையாக அமைவதால்:

β = α அல்லது β = 180° − α.

ஃ cos α = ±cos β = |cos β|,

h = |a| |cos β|.

எனவே இணைகரத்திண்மத்தின் கனஅளவு:

V = Ah = |a| |b × c| |cos β|,

திசையிலி முப்பெருக்கத்தின் வரையறைப்படி, மேலுள்ள கனஅளவு a · (b × c) -ன் தனிமதிப்பிற்குச் சமம்.

$V=\left|a.(b\times c)\right|.$

இத்திசையிலிப் முப்பெருக்கத்தின் தனிமதிப்பை அணிக்கோவையின் தனிமதிப்பாகவும் பின்வருமாறு தரலாம்:

$V=\left|\det {\begin{bmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{bmatrix}}\right|.$

a, b, மற்றும் c -இணைகரத்திண்மத்தின் விளிம்புகளின் நீளங்கள்; α, β, மற்றும் γ -விளிம்புகளுக்கு இடையே உள்ள உட்கோணங்கள் எனில், இணைகரத்திண்மத்திண்மத்தின் கன அளவு:

$V=abc{\sqrt {1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}}.$

தொடர்புள்ள நான்முகி

ஒரு இணைகரத்திண்மத்தின் மூன்று ஒருமுனை விளிம்புகளைத் தனது விளிம்புகளாகக் கொண்ட ஒரு நான்முகியின் கனஅளவு இணைகரத்திண்மத்தின் கனஅளவில் ஆறில் ஒரு பங்காக இருக்கும்.

சிறப்பு வகைகள்

சமச்சீர் தளம் கொண்ட இணைகரத்திண்மங்களில் இரண்டு வகைகள் உள்ளன:

• நான்கு செவ்வக முகங்கள் கொண்டவை.
• இரண்டு சாய்சதுர முகங்களுடன் ஏனைய நான்கு முகங்களில் அடுத்துள்ள இருமுகங்கள் கொண்ட சோடிகள் இரண்டும் ஒன்றுக்கொன்று கண்ணாடி பிம்பங்களாக அமையும்.

ஒரு கனசெவ்வகமானது, செவ்வக முகங்கள் கொண்ட இணைகரத்திண்மமாகும். ஒரு கனசதுரமானது, சதுர முகங்கள் கொண்ட கனசெவ்வகமாகும்.

ஒரு சாய்சதுரத்திண்மமானது, சாய்சதுர முகங்கள் கொண்ட இணைகரத்திண்மமாகும். மூன்றுகோண பட்டமுகத்திண்மமானது சர்வசம சாய்சதுர முகங்கள் கொண்ட சாய்சதுரத்திண்மமாகும்.

மேற்கோள்கள்

• Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, p. 122, 1973. (He define parallelotope as a generalization of a parallelogram and parallelepiped in n-dimensions.)

வெளி இணைப்புகள்

• Weisstein, Eric W., "Parallelepiped", MathWorld.
• Weisstein, Eric W., "Parallelotope", MathWorld.
• Paper model parallelepiped (net)