டேன்ஜெண்ட் (முக்கோணவியல்)
கணிதத்தில் டேன்ஜெண்ட் அல்லது தான்சன் (tangent) சார்பு என்பது ஒரு கோணத்தின் சார்பாகும். கோணங்களின் சார்புகளாக அமையும் ஆறு முக்கோணவியல் சார்புகளில் இது மூன்றாவது சார்பாக வரிசைப்படுத்தப் படுகிறது. ஒரு செங்கோண முக்கோணத்தில், ஒரு கோணத்தின் டேன்ஜெண்ட் மதிப்பு, அக்கோணத்தின் எதிர்ப் பக்கத்திற்கும் அடுத்துள்ள பக்கத்திற்குமுள்ள விகிதமாகும். ஓரலகு வட்டம், சாய்வு, முடிவிலாத்தொடர் முதலியவை வாயிலாகவும் மற்றும் வகைக்கெழுச் சமன்பாடுகளின் தீர்வாகவும் டேன்ஜெண்ட் சார்பை வரையறுக்கலாம்.
செங்கோண முக்கோணத்தில் வரையறை[தொகு]

வடிவொத்த முக்கோணங்களின் ஒத்தபக்கங்களின் விகிதங்கள் சமமாக இருக்கும் என்ற உண்மையிலிருந்து, ஒரு முக்கோணத்தின் பக்க நீளங்களுக்கும் கோண அளவுகளுக்கும் தொடர்பு இருக்கும் என்ற கருத்து அறியப்படுகிறது. இரு செங்கோண முக்கோணங்களில் ஒன்றின் செம்பக்கம் மற்றதன் செம்பக்க நீளத்தைப் போல இருமடங்கு எனில் மற்ற பக்கங்களும் அவ்வாறே அமையும். இந்த பக்க விகிதங்களைத்தான் முக்கோணவியல் சார்புகள் தருகின்றன.
ஒரு செங்கோண முக்கோணத்தின் கோணம் A -ன் முக்கோணவியல் சார்புகளை வரையறுக்க அம்முக்கோணத்தின் பக்கங்களைப் பின்வருமாறு அழைக்கலாம்:
- செம்பக்கம் (அல்லது கர்ணம்) (hypotenuse):
செங்கோணத்திற்கு எதிர்ப்பக்கம். இதன் அளவு h. ஒரு செங்கோண முக்கோணத்தில் செம்பக்கந்தான் மூன்று பக்கங்களிலும் நீளமானது.
- எதிர்ப்பக்கம் (opposite):
நாம் எடுத்துக்கொண்ட கோணம் A -க்கு எதிரில் அமையும் பக்கம். இதன் நீளம் a.
- அடுத்துள்ள பக்கம் (adjacent):
செங்கோணம் மற்றும் நாம் எடுத்துக்கொண்ட கோணம் இரண்டிற்கும் ( A மற்றும் C) பொதுவான பக்கம். இதன் நீளம் b.
டேன்ஜெண்ட் சார்பு:
செங்கோண முக்கோணத்தின் ஒரு கோணத்தின் டேன்ஜெண்ட் மதிப்பு, அக்கோணத்தின் எதிர்ப்பக்கத்திற்கும் அடுத்துள்ள பக்கத்திற்குமுள்ள விகிதமாகும்.
A கோணத்தைக் கொண்ட அனைத்து செங்கோண முக்கோணங்களிலும் இவ்விகிதத்தின் மதிப்பு ஒரே மதிப்புடையதாய் அமையும். அச்செங்கோண முக்கோணங்கள் எல்லாம் வடிவொத்த முக்கோணங்கள் என்பதால் அவற்றின் பக்க அளவுகள் வெவ்வேறாக இருந்தாலும் அவற்றின் அவ்வேறுபாடு இவ்விகிதத்தின் மதிப்பைப் பாதிப்பதில்லை.
வரையறை- சாய்வு வாயிலாக[தொகு]
செங்கோண முக்கோணங்களின் மூலம் வரையறுப்பது போல ஒரு கிடைமட்டக்கோட்டுடன் தொடர்புடைய ஒரு கோட்டுத்துண்டின் எழுச்சி (rise), ஓட்டம்(run), சாய்வு ஆகியவற்றின் மூலமாகவும் முக்கோணவியல் சார்புகளை வரையறுக்கலாம்.
எடுத்துக்கொள்ளப்பட்ட கோட்டுத்துண்டின் நீளம் 1 அலகு என்க. அக்கோட்டுத்துண்டு ஒரு குறிப்பிட்ட கிடைமட்டக்கோட்டுடன் உருவாக்கும் கோணம் A என்க. இக்கோணத்தின்:
- டேன்ஜெண்ட் மதிப்பு, கோட்டுத்துண்டின் சாய்வுக்குச் சமம்.
- tanA = சாய்வு
கோட்டுத்துண்டின் நீளம் சாய்வின் மதிப்பை பாதிப்பதில்லை.
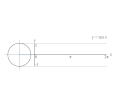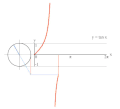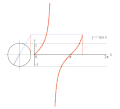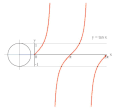
வரையறை- ஓரலகு வட்டம் வாயிலாக[தொகு]
ஆறு முக்கோணவியல் சார்புகளையும் ஓரலகு வட்டத்தைக் கொண்டு வரையறுக்கலாம். ஓரலகு வட்டம் என்பது ஆதிப்புள்ளியை மையமாகவும் ஆரம் 1 அலகும் கொண்ட வட்டமாகும். நடைமுறைக் கணக்கீடுகளுக்கு ஓரலகு வட்டத்தின் மூலமான வரையறை அவ்வளவாகப் பொருந்தாவிடினும், (0, π/2 ) -ல் அமையும் கோணங்களுக்கு மற்றுமல்லாது அனைத்து மெய்யளவு கோணங்களுக்கும் பொருத்தமாக அமையும்.
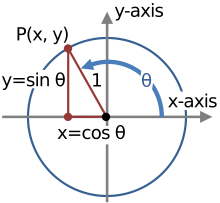
x-அச்சின் நேர்மப் பகுதியோடு, ஆதிப்புள்ளியில் θ கோணம் உண்டாக்கும் ஒரு கோடு ஓரலகு வட்டத்தை சந்திக்கிறது என்க. அந்த சந்திக்கும் புள்ளியின் x- மற்றும் y-அச்சுதூரங்கள் முறையே cos θ மற்றும் sin θ -க்குச் சமம். செங்கோண முக்கோண முறை வரையறைப்படியும் இதை உணரலாம். வெட்டும் புள்ளியின் அச்சுதூரங்கள்: (x, y) என்க. ஓரலகு வட்டத்தின் ஆரம் செங்கோண முக்கோணத்தின் செம்பக்கம். எனவே செம்பக்கத்தின் அளவு 1 அலகு.
 |
 |
 |
-
ஓரலகு வட்டத்தைப் பயன்படுத்தி y = tan(x) சார்பின் வரைபடம் வரைதலின் அசைப்படம்.
முடிவிலாத் தொடரின் வாயிலாக[தொகு]
டெயிலரின் விரிவுக் கோட்பாட்டைப் பயன்படுத்திப் பின்வரும் முற்றொருமையை, எல்லா மெய்யெண்கள் x -க்கும் உண்மையெனக் காட்டலாம்.[1][2]
- Bn: n -ஆம் பெர்னெளலியின் எண்.
வகைக்கெழுச் சமன்பாட்டின் வாயிலாக[தொகு]
- என்ற வகைக்கெழுச் சமன்பாட்டின் தனித்த தீர்வு டேன்ஜெண்ட் சார்பு
இது நிறைவு செய்யும் நிபந்தனை y(0) = 0. டேன்ஜெண்ட் சார்பு இந்த வகைக்கெழுச் சமன்பாட்டினை நிறைவு செய்யும் என்பதற்கான நிறுவல் உள்ளது.[3]
முற்றொருமைகள்[தொகு]
-ன் அனைத்து மதிப்புகளுக்கும் பின்வரும் முற்றொருமைகள் மெய்யாகும்:
- ஏனைய ஐந்து முக்கோணவியல் சார்புகளின் வாயிலாக:
- =
- =
- =
- =
- =
தலைகீழி[தொகு]
டேன்ஜெண்ட் சார்பின் தலைகீழிச் சார்பு கோடேன்ஜெண்ட் சார்பு.
tan(A) -ன் தலைகீழி cot(A):
நேர்மாறு[தொகு]

டேன்ஜெண்ட் சார்பின் நேர்மாறுச் சார்பு:
arctan அல்லது (tan−1).
k ஏதாவதொரு முழு எண் எனில்:
மேலும்:
- .
நுண்கணிதம்[தொகு]
டேன்ஜெண்ட் சார்பு:
நுண்கணிதத்தில் இச்சார்பின்:
C, தொகையீட்டு மாறிலி.
மேற்கோள்கள்[தொகு]
- ↑ See Ahlfors, pages 43–44.
- ↑ Abramowitz; Weisstein.
- ↑ Needham, p. Visual Complex Analysis. பன்னாட்டுத் தரப்புத்தக எண்:0198534469.