முக்கோணம்
இந்தக் கட்டுரையில் மேற்கோள்கள் அல்லது உசாத்துணைகள் எதுவும் இல்லை. |
| முக்கோணம் | |
|---|---|
 ஒரு முக்கோணம் | |
| விளிம்புகள் மற்றும் உச்சிகள் | 3 |
| சிலாஃப்லி குறியீடு | {3} (சமபக்க முக்கோணிக்கு) |
| பரப்பளவு | பல வழிகள் உள்ளன; கீழே காண்க |
| உட்கோணம் (பாகை) | 60° (சமபக்க முக்கோணி) |
முக்கோணம் அல்லது முக்கோணி (Triangle) என்பது மிகச் சிறிய எண்ணிக்கையுள்ள நேர்கோடுகளால் ஒரு பரப்பை அடைக்க வல்ல ஓர் அடிப்படையான வடிவம். வடிவக்கணித (கேத்திர கணித) அடிப்படை வடிவங்களில் ஒன்று. பெயருக்கு ஏற்றாற் போல் இவ்வடிவம் மூன்று கோணங்களையும் மூன்று உச்சிகளையும் நேர்கோடுகளாலான மூன்று பக்கங்களையும் கொண்ட, ஒரு தட்டையான இரு பரிமாண உருவமாகும்.
யூக்களிடியன் வடிவியலில் ஒரே நேர்கோட்டில் அமையாத மூன்று புள்ளிகள் ஒர் குறித்த முக்கோணத்தையும் தளத்தையும் வரையறுக்கின்றன.(இருபரிமாண யூக்ளிடியன் வெளி).
முக்கோணத்தின் வகைகள்[தொகு]
பக்க நீளங்கள் சார்பாக[தொகு]
முக்கோணங்களை, அவற்றின் பக்கங்களின் நீளங்கள் தொடர்பில் வகைப்படுத்தமுடியும். அவை பின்வருமாறு:-
- எல்லாப் பக்கங்களும் ஒரே அளவு நீளமுள்ளதாக இருப்பின் அது, சமபக்க முக்கோணம் எனப்படும். ஒரு சமபக்க முக்கோணம், சமகோண (எல்லாக் கோணங்களும் சமம்) முக்கோணமாகவும் இருக்கும்.
- இரண்டு பக்கங்கள் சம அளவுள்ளதாக இருக்கும் முக்கோணம் இருசமபக்க முக்கோணம் எனப்படும். இருசமபக்க முக்கோணமொன்றில் இரண்டு கோணங்களும் ஒன்றுக்கொன்று சமமாக இருக்கும்.
- ஒன்றுக்கொன்று சமனில்லாத மூன்று பக்கங்களையுடைய முக்கோணம் சமனில் பக்க முக்கோணம் ஆகும். இவ்வகை முக்கோணத்தின் ஏதாவது இரண்டு கோணங்களும் சமனற்றவையாகும்.
 |
 |
 |
| சமபக்கம் | இருசமபக்கம் | சமனில் பக்கம் |
உட்கோணங்கள் சார்பாக[தொகு]
முக்கோணங்களின் மிகப்பெரிய உட்கோணத்தின் அடிப்படையிலும், முக்கோணங்களை வகைப்படுத்தலாம்.
- ஒரு கோணம் செங்கோணமாக (90 பாகை அல்லது π/2 ரேடியன் அளவு) அமைந்துள்ள முக்கோணங்கள், செங்கோண முக்கோணங்கள் எனப்படுகின்றன. செங்கோணத்துக்கு எதிராக உள்ள பக்கம் செம்பக்கம் என அழைக்கப்படும். இதுவே செங்கோண முக்கோணமொன்றின் மிக நீளமான பக்கமாகும்.
- முக்கோணத்திலுள்ள யாதேனும் ஒரு கோணம் செங்கோணத்திலும் பெரிதாக இருந்தால் அது விரிகோண முக்கோணம் எனப்படும்.
- எல்லாக் கோணங்களும் செங்கோணத்திலும் சிறிதாக இருப்பின் அத்தகைய முக்கோணம் ஒரு கூர்ங்கோண முக்கோணம் ஆகும்.
 |
 |
 |
| செங்கோணம் | விரிகோணம் | குறுங்கோணம் |
| சாய்வுக்கோணம் | ||
அடிப்படை உண்மைகள்[தொகு]
முக்கோணம் மூன்று பக்கங்களுடைய ஒரு பல்கோணமாகும்.
ஒரு முக்கோணத்தைச் சீராக விரிவடையச் செய்வதன் மூலம் மற்றைய முக்கோணத்தைப் பெறமுடியுமெனில், அவ்விரு முக்கோணங்களும் ஒத்த முக்கோணங்கள் எனக் கூறப்படுகின்றன. இதில் அம்முக்கோணங்களின் பக்கங்கள் விகிதசமனானவை. முக்கோணமொன்றின் நீளமான பக்கம், ஒத்த முக்கோணமொன்றின் நீளமான பக்கத்தின் இரண்டு மடங்காயின், முதல் முக்கோணத்தின் சிறிய பக்கமும் மற்ற முக்கோணத்தின் சிறியபக்கத்தின் இரண்டு மடங்காக இருக்கும். மூன்றாவது பக்கமும் அவ்வாறே மற்றதன் இரண்டு மடங்காகக் காணப்படும். அத்துடன் முதல் முக்கோணத்தின் ஏதாவது இரண்டு பக்கங்களுக்கிடையேயான விகிதம், இரண்டாவது முக்கோணத்தின் ஒத்த பக்கங்களுக்கிடையேயான விகிதத்துக்குச் சமனாகும். இரண்டு முக்கோணங்களின் ஒத்த கோணங்கள் ஒன்றுக்கொன்று சமனாக இருப்பின் மட்டுமே அவ்விரு முக்கோணங்களும் ஒத்தவையாக இருக்கும்.
செங்கோண முக்கோணங்களையும் ஒத்த முக்கோணங்கள் பற்றிய எண்ணக்கருவையும் பயன்படுத்தி, சைன், கோசைன் போன்ற திரிகோணகணிதச் சார்புகள் வரையறுக்கப்பட்டுள்ளன.
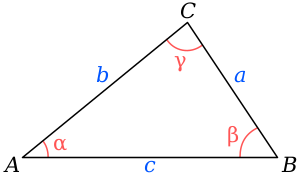
A, B, C என்பவற்றை உச்சிகளாகவும் α, β, γ என்பவற்றைக் கோணங்களாகவும் a, b, c ஆகியவற்றைப் பக்கங்களாகவும் கொண்ட முக்கோணத்தில், பக்கம் a கோணம் α வுக்கும், உச்சி A க்கும் எதிரேயுள்ளது. இதே போலவே ஏனைய பக்கங்களுமாகும். எனின்,
α, β, γ கோணங்களின் கூட்டுத்தொகை இரண்டு செங்கோணங்களுக்குச் சமன் அல்லது 180 பாகை ஆகும். (α + β + γ = 180 பாகை).
முக்கோணம் தொடர்பான தேற்றங்களில், பைதகரசின் தேற்றம் முக்கியமான ஒன்று. இது ஒரு செங்கோண முக்கோணத்தின் பக்கங்களுக்கிடையேயான தொடர்பைக் காட்டுகிறது. இதன்படி, ஒரு செங்கோண முக்கோணத்தில், செம்பக்கத்தின் வர்க்கம், ஏனைய இரண்டு பக்கங்களின் வர்க்கங்களின் கூட்டுத்தொகைக்குச் சமன். மேலேயுள்ள முக்கோணத்தில் γ ஒரு செங்கோணமாக இருந்தால்,
பைதகரசின் தேற்றத்தை எல்லா முக்கோணங்களுக்கும் பொருந்தக்கூடியவகையில் பொதுமைப்படுத்த முடியும். இது கோசைன் விதி என அழைக்கப்படும். இதன்படி:
முக்கோணம் தொடர்பான சைன் விதியின் படி,
இயல்பொத்தவை, ஒருங்கிசைவானவை[தொகு]
ஒரு முக்கோணத்தின் மூன்று கோணங்களும் அவற்றுக்கு ஒத்த மற்றய முக்கோணத்தின் கோணங்களுக்குச் சமனாக இருப்பின் அவை இயல்பொத்தவை அல்லது வடிவொத்தவை எனப்படும். அந்த முக்கோணங்களின் ஒத்த பக்கங்களின் நீளங்களிற்கிடையேயான விகிதங்கள் சமனாக இருக்கும், இந்தப்பண்பு இயல்பொப்புமையை நிறுவ போதுமானது.
இயல்பொத்த முக்கோணங்களின் சில பண்புகள்:
- இரு முக்கோணங்களிற்கிடையே ஒத்த கோணங்கள் சமனாக இருப்பின் அந்த முக்கோணங்கள் இயல்பொத்தவை.
- இரு முக்கோணங்களின் மூன்று ஒத்த பக்கங்களிற்கிடையேயான விகிதங்களும் சமனாக இருப்பின் அவை இயல்பொத்தவை.
- இரு முக்கோணங்களின் இரு ஒத்த பக்கங்களிற்கிடையேயான விகிதங்கள் சமனாகவும் அவற்றுடன் தொடர்புடைய கோணங்கள் சமனாகவும் இருப்பின் அவை இயல்பொத்தவை.
அளவிலும் வடிவத்திலும் சர்வ சமனாக இருக்கும் இரு முக்கோணங்கள் ஒருங்கசைவானவை எனப்படும். அனைத்து ஒத்தசோடி உட்கோணங்களும் சமனானவை, அனைத்து ஒத்தசோடிப் பக்கங்களும் ஒரே நீளத்தை கொண்டிருக்கும்.
இரு சோடி முக்கோணங்கள் ஒருங்கிசைவதற்கான நிபந்தனைகள்:
ப.கோ.ப: முக்கோணத்தின் இரு பக்கங்களின் நீளங்கள் அதற்கொத்த மற்றய முக்கோணத்தின் இரு பக்கங்களின் நீளத்திற்கு சமனாக இருக்க வேண்டும், அந்தப் பக்கங்களிற்கிடையேயான கோணம் இரு முக்கோணங்களிலும் சமனாக இருக்க வேண்டும்.
கோ.ப.கோ: முக்கோணத்தின் இரு கோணங்களும் அவற்றிற்கிடையேயான பக்கமும் மற்றய முக்கோணத்தின் இரு கோணங்களிற்கும் அவற்றிற்கிடையேயான பக்கத்திற்கும் சமனாக இருக்க வேண்டும்.
ப.ப.ப:முக்கோணத்தின் மூன்று பக்கங்களின் நீளங்களும் மற்றய முக்கோணத்தின் அதற்கொத்த பக்கங்களின் நீளங்களிற்கு சமனாக இருக்கவேண்டும்.
கோ.கோ.ப: ஒரு முக்கோணத்தின் இரு கோணங்களும் ஒரு பக்கமும் மற்றய முக்கோணத்தின் இரு கோணங்களிற்கும் குறித்த பக்கத்திற்கும் சமனாக இருக்கவேண்டும்.
செ.ப: இரு செங்கோண முக்கோணிகளில் ஒரு முக்கோணியின் செம்பக்கமும், ஒரு பக்கமும் முறையே மற்றய முக்கோணியின் செம்பக்கத்திற்கும் ஒரு பக்கத்திற்கும் சமனாக இருக்கவேண்டும்.
செங்கோண முக்கோணி[தொகு]

பைத்தகரசின் தேற்றத்தின் படி யாதயினும் ஓர் செங்கோண முக்கோணியில் செம்பக்க நீளத்தின் வர்க்கமானது மற்றய பக்க நீளங்களின் வர்கங்களின் கூட்டுத்தொகைக்கு சமனாகும். செம்பக்க நீளத்தை c எனவும் மற்றய பக்க நீளங்களை a, b எனக்கொண்டால் தேற்றத்தின் படி
இதன் மறுதலையும் உண்மையானது, ஒரு முக்கோணத்தின் பக்கங்கள் மேற்படி சமன்பாட்டை சரி செய்தால் பக்கம் c இற்கு எதிர்ப்பக்கத்தில் செங்கோணம் அமைந்திருக்கும்.
செங்கோண முக்கோணத்தைப் பற்றிய வேறுசில உண்மைகள்:
- செங்கோண முக்கோணியில் கூர்ங்கோணங்கள் ஒன்றிற்கொன்று நிரப்புக்கோணங்கள்.
- செங்கோண முக்கோணியின் செம்பக்கமல்லாத பக்கங்களின் நீளங்கள் சமனாயின் அவற்றின் கோணங்கள் 45 பாகையாக இருக்கும்.
முக்கோணத்துடன், புள்ளிகள், கோடுகள், வட்டங்கள் என்பவற்றின் தொடர்பு[தொகு]
முக்கோணத்தின் பரப்பைக் கணித்தல்[தொகு]
ஒரு முக்கோணத்தின் பரப்பளவு பின்வரும் சமன்பாட்டினால் தரப்படுகின்றது.
- S = 1/2 × அடி × உயரம்
இங்கு S முக்கோணத்தின் பரப்பளவாகும்.
முக்கோணங்களின் பரப்பளவைக் கணிக்கப் பயன்படும் இன்னொரு சமன்பாடு எரோனின் வாய்ப்பாடு பின்வருமாறு:-
இங்கே s = 1/2 (a + b + c) அதாவது முக்கோணத்தின் சுற்றளவின் அரைவாசி.
மாற்றாக
- S = sr
இங்கே s மேலே வரையறுக்கப்பட்டபடியும், r முக்கோணத்தின் உள்வட்டத்தின் ஆரையுமாகும்.