சதுரம்
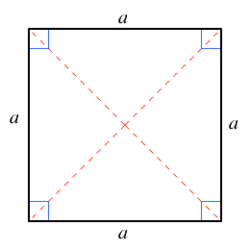
சதுரம், கேத்திரகணித அடிப்படை வடிவங்களில் ஒன்று. இது, நான்கு உச்சிகளையும், சம அளவிலான நான்கு கோட்டுத்துண்டுகளை பக்கங்களாகவும் கொண்ட, ஒரு இரு பரிமாண உருவமாகும். சதுரம் ஓர் ஒழுங்கு நாற்கரம் ஆகும்.
அடிப்படை உண்மைகள்[தொகு]
- சதுரம் நான்கு சமபக்கங்களுடைய ஒரு பல்கோணமாகும்.
- ABCD சதுரத்தில்
- நான்கு கோணங்களின் அளவுகள் சமமாகவும் ஒவ்வொன்றும் 90 பாகை அளவாகவும் இருக்கும்.
- பாகைகள்.
- சதுரத்தின் இரு மூலைவிட்டங்களும் (கோணல் கோடுகள்) சமநீளமுள்ளவை.
- ஒரு சதுரத்தின் ஒரு பக்கத்தின் நீளம் a எனில், அதன் சுற்றளவு a யின் நான்கு மடங்கு ஆகும்.
- மூலைவிட்டத்தின் நீளம்:
விளக்கம்:
சதுரத்தின் ஒவ்வொரு கோணமும் செங்கோணம் என்பதால் இரு அடுத்துள்ள பக்கங்களும் ஒரு மூலைவிட்டமும் ஒரு செங்கோண முக்கோணத்தை அமைக்கின்றன. சதுரத்தின் பக்க அளவு a, மூலைவிட்டத்தின் நீளம் d எனில், பித்தகோரசு தேற்றத்தின்படி:
சதுரத்தின் பரப்பு[தொகு]

ஒரு சதுரத்தின் பரப்பளவு அதன் ஒரு பக்க அளவின் வர்க்கத் தொகையால் தரப்படுகிறது. உதாரணத்திற்கு, ஒரு சதுரத்தின் பக்க அளவு 5 மீட்டர் என்றால், அதன் பரப்பளவு 5 x 5 = 25 சதுர மீட்டர் ஆகும். 5 மீட்டர் பக்க நீளமுள்ள சதுரத்தை 1 மீட்டர் பக்க நீளமுள்ள சிறுசிறு சதுரங்களாகப் பிரித்தால் மொத்தம் 25 சிறு சதுரங்கள் கிடைக்கின்றன.
பொதுவாகச் சதுரத்தின் பரப்பு a எனில்:
மூலைவிட்டத்தின் மூலமாகவும் சதுரத்தின் பரப்பளவைக் காணலாம். சதுரத்தின் மூலைவிட்டத்தின் நீளம் d எனில் அச்சதுரத்தின் பரப்பளவு:
சதுரத்தின் சுற்றுவட்ட ஆரம் R எனில்,
எனவே சதுரத்தின் பரப்பளவு:
சதுரத்தின் உள்வட்ட ஆரம் r எனில்,
எனவே சதுரத்தின் பரப்பளவு:
அடுக்கு இரண்டு என்பது சதுரத்தின் பரப்பளவாக எடுத்துக் கொள்ளப்பட்டதால்தான் அடுக்கு இரண்டானது ஆங்கிலத்தில் ஸ்கொயர் என அழைக்கப்பட்டது.
சமன்பாடுகள்[தொகு]

கார்ட்டீசியன் ஆள்கூற்று முறைமையில் ஆதிப்புள்ளியை மையமாகவும் 2 அலகுகள் பக்கநீளமும் கொண்ட சதுரத்தின் உச்சிகளின் ஆயதொலைவுகள்: (±1, ±1). சதுரத்தின் உட்புறம் அமையுமொரு புள்ளிகளின் ஆயதொலைவுகள் (xi, yi) , −1 < xi < 1, −1 < yi < 1 ஆகும். இச் சதுரத்தின் சமன்பாடு:
- , அதாவது "x2 அல்லது y2, இரண்டில் எது பெரியதோ அதன் மதிப்பு 1 ஆக இருக்கும்."
இச்சதுரத்தின் சுற்றுவட்டத்தின் ஆரம் மூலைவிட்டத்தின் நீளத்தில் பாதியாக இருக்கும். அதாவது
சுற்றுவட்டத்தின் ஆரம்:
- .
சுற்றுவட்டத்தின் சமன்பாடு:
சதுரத்தின் மற்றொரு சமன்பாடு:
சதுரத்தின் மையம்: (a, b) மற்றும் கிடைமட்ட அல்லது குத்து ஆரம் r எனில் அச்சதுரத்தின் சமன்பாடு:
பண்புகள்[தொகு]
சதுரம் என்பது சாய்சதுரம், பட்டம், இணைகரம், நாற்கரம் மற்றும் செவ்வகம் ஆகியவற்றின் சிறப்பு வகையாகும். எனவே இவ்வடிவவியல் வடிவங்களின் பண்புகள் சதுரத்திற்கும் உண்டு:[1]
- சதுரத்தின் எதிரெதிர் பக்கங்கள் இணையாகவும் சமமாகவும் இருக்கும்.
- சதுரத்தின் நான்கு கோணங்களும் சமம். (ஒவ்வொன்றும் 360°/4 = 90° க்குச் சமம்.)
- சதுரத்தின் நான்கு பக்கங்களும் சமம்.
- இரு மூலைவிட்டங்களும் சம நீளமுள்ளவை.
- சதுரத்தின் இரு மூலைவிட்டங்களும் ஒன்றையொன்று இருசமக் கூறிடும். மேலும் செங்குத்தாக வெட்டிக்கொள்ளும்.
- சதுரத்தின் கோணங்களை அதன் மூலைவிட்டங்கள் இருசமக்கூறிடும்.
பிற விவரங்கள்[தொகு]
- ஒரு சதுரத்தின் மூலைவிட்டங்கள் ஒவ்வொன்றின் நீளமும் அச்சதுரத்தின் பக்கநீளத்தைப்போல் (கிட்டத்தட்ட 1.414) மடங்காகும். விகிதமுறா எண் என நிறுவப்பட்ட முதல் எண்
- கோணங்களை இருசமக்கூறிடும் சம நீளமுள்ள மூலைவிட்டங்கள் கொண்ட இணைகரமாகச் சதுரத்தை வரையறுக்கலாம்.
- செவ்வகமாகவும் சாய்சதுரமாகவும் அமையக்கூடிய வடிவவியல் வடிவமாகச் சதுரத்தைக் கருதலாம்.
- சதுரத்தைச் சுற்றி அதன் நான்கு உச்சிகளின் வழியாகச் செல்லும் வட்டத்தின் (சுற்று வட்டம்) பரப்பளவு சதுரத்தின் பரப்பைப்போல் (கிட்டத்தட்ட 1.571) மடங்காகும்.
- சதுரத்துக்குள் அதன் பக்கங்களைத் தொட்டவாறு வரையப்பட்ட வட்டத்தின் (உள்வட்டம்) பரப்பளவு சதுரத்தின் பரப்பளவைப்போல் (கிட்டத்தட்ட 0.7854) மடங்காகும்.
- ஒரு சதுரத்துடன் சம சுற்றளவுடைய எந்தவொரு நாற்கரத்தின் பரப்பளவையும் விட சதுரத்தின் பரப்பளவு பெரியது.[2]
- சதுரம் அதிக சமச்சீருள்ள ஒரு வடிவம். ஒரு சதுரத்திற்கு நான்கு பிரதிபலிப்பு சமச்சீர் அச்சுகளும் நான்கு கிரம சுழற்சி சமச்சீரும் (through 90°, 180° , 270° கோண சுழற்சிகள்) உள்ளது. சதுரத்தின் சமச்சீர் குலம், ஒரு இருமுகக் குலம் ( D4).
- ABCD சதுரத்தின் பக்கங்கள் AB, BC , CD, DA ஆகியவற்றை உள்வட்டம் தொடும் புள்ளிகள் முறையே E , F , G , H மற்றும் உள்வட்டத்தின் மேலுள்ள ஒரு புள்ளி P எனில்[3]:
தமிழ்ப் பெயர்[தொகு]
- நாலாரம் ( நாலு + ஆரம் )
- நாலியாரம் ( நாலி+ ஆரம் )
- நால்வாரி ( வரி -> வாரி )
- நால்வாரிகை ( வரி -> வாரி )
வரைதல்[தொகு]
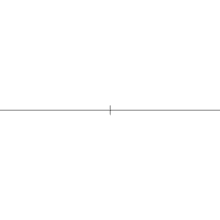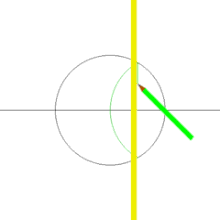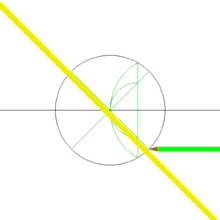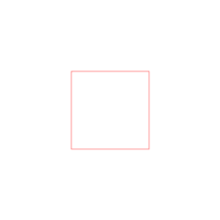
கவராயமும் நேர்விளிம்பும் மட்டும் கொண்டு சதுரம் வரையும் விதம் இங்குள்ள அசைபடத்தில் காட்டப்பட்டுள்ளது.
- வரைமுறை
- நேர்விளிம்பு கொண்டு ஒரு நேர்கோடு வரைக.
- கவராயம் கொண்டு இக்கோட்டின் மீதமைந்த ஏதேனுமொரு புள்ளியை மையமாகவும் ஒரு குறிப்பிட்ட ஆரமும் கொண்ட வட்டம் வரைக.
- இவ்வட்ட மையத்துக்கும் வட்டமையம் கோட்டை வெட்டும் புள்ளிக்கும் இடைப்பட்ட தூரத்தை ஆரமாகவும், வட்டம் கோட்டை வெட்டும் புள்ளியை மையமாகவும் கொண்டு ஒரு வட்டம் வரைக.
- இந்த இரண்டாவது வட்டம் முதல் வட்டத்தை வெட்டும் இரு புள்ளிகளை இணைத்து ஒரு கோட்டுத்துண்டு வரைக.
- இந்த கோட்டுத்துண்டு முதலில் வரைந்த கோட்டை சந்திக்கும் புள்ளியை மையமாகவும், இப்புள்ளிக்கும் முதல் வட்டத்தின் மையத்துக்கும் இடைப்பட்ட தூரத்தை ஆரமாகவும் கொண்டு மூன்றாவது வட்டமொன்று வரைக.
- இந்த வட்டம் கோட்டுத்துண்டை இரு புள்ளிகளில் சந்திக்கும்.
- இந்த இரு புள்ளிகள் ஒவ்வொன்றையும் முதலில் வரைந்த வட்ட மையத்துடன் இணைத்து வரையப்படும் கோட்டை இருபுறங்களிலும் நீட்டித்தால், அக்கோடுகள் இரண்டும் முதல் வட்டத்தைச் சந்திக்கும் நான்கு புள்ளிகளும் ஒரு சதுரத்தை உருவாக்கும்.























