ஐங்கோணம்
| ஒழுங்கு ஐங்கோணம் | |
|---|---|
 படம் | |
| விளிம்புகள் மற்றும் உச்சிகள் | 5 |
| சிலாஃப்லி குறியீடு | {5} |
| கோஎக்சிட்டர்-டின்க்கின் படம் | |
| சமச்சீர் குலம் | இருமுகக் குலம் (D5) |
| உட்கோணம் (பாகை) | 108° |
| பண்புகள் | குவிவு, வட்டத்துக்குள் பலகோணம், சமபக்கம் கொண்டது, சமகோணமுடையது, விளிம்பு-கடப்புடையது |
வடிவவியலில் ஐங்கோணம் (pentagon) என்பது ஐந்து பக்கங்களைக் கொண்ட ஒரு பலகோணமாகும். ஒரு ஐங்கோணத்தின் ஐந்து பக்கங்களும் சம அளவுடன் இருந்தால் அந்த ஐங்கோணம் ஒழுங்கு ஐங்கோணம் அல்லது சீர் ஐங்கோணம் (regular pentagon) எனப்படும். ஒரு ஐங்கோணத்தின் அனைத்து (ஐந்து) உட்கோணங்களின் கூட்டுத்தொகை 540°. கிரேக்க மொழியில் எண் ஐந்தைக் குறிக்கும் சொல்லான pente -யிலிருந்து ஐங்கோணத்தின் ஆங்கிலப் பெயர் pentagon தோன்றியுள்ளது. ஒரு ஐங்கோணம் தனக்குள்ளாக வெட்டிக் கொள்வதாகவும் அமையலாம். நட்சத்திர ஐங்கோணம் இவ்வகையைச் சேர்ந்தது.
ஒழுங்கு ஐங்கோணம்[தொகு]
ஒரு ஒழுங்கு ஐங்கோணத்தின் ஐந்து பக்கங்களின் அளவுகளும் சமமாகவும் ஒவ்வொரு உட்கோணத்தின் அளவும் 108° -ஆகவும் இருக்கும். ஒழுங்கு ஐங்கோணத்திற்கு 5 சமச்சீர் பிரதிபலிப்புக் கோடுகளும் 5 வரிசையுடைய சமச்சீர் சுழற்சிகளும் (72°, 144°, 216° மற்றும் 288°) உண்டு. ஒரு ஒழுங்கு ஐங்கோணத்தின் மூலைவிட்டங்கள் அதன் பக்கங்களுடன் தங்க விகிதத்தில் அமைகின்றன.
ஒரு ஒழுங்கு குவிவு ஐங்கோணத்தின் பக்க அளவு t எனில் அதன் பரப்பு காணும் வாய்ப்பாடு:
R, அலகு ஆரமுள்ள ஒரு வட்டத்துக்குள் வரையப்படும் ஒழுங்கு ஐங்கோணத்தின் பக்க நீளம் t :
பரப்பு காணும் வாய்ப்பாட்டை தருவித்தல்[தொகு]
எந்தவொரு ஒழுங்கு பலகோணத்தின் பரப்பு வாய்ப்பாடு:
இங்கு P பலகோணத்தின் சுற்றளவு, a -பலகோணத்தின் மையத்திலிருந்து அதன் ஒரு பக்கத்தின் நடுப்புள்ளிக்கு வரையப்படும் நடுக்கோட்டின் நீளம். ஐங்கோணத்திற்கான இவற்றின் மதிப்புகளை பரப்பு வாய்ப்பாட்டில் பிரதியிட:
t -ஒழுங்கு ஐங்கோணத்தின் பக்க நீளம்.
மூலைவிட்ட நீளம் காணும் வாய்ப்பாட்டை தருவித்தல்[தொகு]
ஒழுங்கு ஐங்கோணத்தின் மூலைவிட்டமும் (D) பக்கமும் (T) தங்க விகிதத்தில் அமையும் என்ற உண்மையைப் பயன்படுத்த:
எனவே மூலைவிட்டத்தின் நீளம்:
சுற்றுவட்டத்திலிருந்து உச்சிகளுக்கு வரையப்படும் நாண்கள்[தொகு]
வரிசையாக A, B, C, D, E உச்சிகளுடைய ஒரு ஒழுங்கு ஐங்கோணம் ஒரு வட்டத்துக்குள் வரையப்பட்டால்:
B மற்றும் C புள்ளிகளுக்கிடையே வட்டத்தின்மீது அமையும் புள்ளி P.
நட்சத்திர ஐங்கோணம்[தொகு]

நட்சத்திர வடிவில் அமையும் ஒழுங்கு ஐங்கோணமானது நட்சத்திர ஐங்கோணம் (pentagram) எனப்படும். இதன் Schläfli குறியீடு {5/2} ஆகும். இச்சிறப்பு வடிவத்தின் பக்கங்கள் ஒழுங்கு குவிவு ஐங்கோணத்தின் மூலைவிட்டங்களாக அமையும். எனவே இவ்விரண்டு வடிவங்களின் பக்கங்கள் தங்க விகிதத்தில் இருக்கும்.
ஒழுங்கு ஐங்கோணம் வரையும் முறை[தொகு]
ஒரு ஒழுங்கு ஐங்கோணம் வரைவதற்கு பல முறைகள் உள்ளன. அவற்றில் சில கீழே தரப்பட்டுள்ளன.
யூக்ளிடின் வரைமுறை[தொகு]
கவராயம் மற்றும் அளவுகோலைப் பயன்படுத்தி ஒரு ஒழுங்கு ஐங்கோணத்தை தரப்பட்ட வட்டத்துக்குள்ளாக அல்லது தரப்பட்ட ஒரு விளிம்பினைக் கொண்டு வரையலாம். இந்த வரைமுறையை தனது எலிமெண்ட்ஸில் யூக்ளிட் விளக்கியுள்ளார் (கிமு.300).[1]
ரிச்மாண்டின் வரைமுறை[தொகு]
ஒரு தரப்பட்டுள்ள வட்டத்துக்குள் ஒழுங்கு ஐங்கோணம் வரையும் மற்றொரு முறை:[2]

- வட்டத்தின் மீது ஒரு புள்ளியைத் தேர்ந்தெடுக்கவும். இது நாம் வரையப்போகும் ஒழுங்கு ஐங்கோணத்தின் ஒரு உச்சியாக இருக்கும்.
- அப்புள்ளியின் வழியே வட்டத்திற்கு ஒரு விட்டம் வரைக.
- இந்த விட்டத்திற்கு செங்குத்தான ஆரம் வரைக.
- இந்த ஆரத்தை இருசமக்கூறிடக் கிடைக்கும் நடுப்புள்ளியையும் வட்டத்தை நாம் வரைந்த விட்டம் சந்திக்கும் புள்ளியையும் இணைத்து ஒரு கோடு வரைக
- இக்கோட்டால் உண்டாகும் கோணத்தை இருசமக்கூறிடும் கோடு விட்டத்தைச் சந்திக்கட்டும்.
- இச்சந்திப்புப் புள்ளியிலிருந்து ஆரத்துக்கு இணையாக வரையப்படும் கோடு வட்டத்தைச் சந்திக்கட்டும்.
- இச்சந்திப்பு புள்ளியையும் ஏற்கனவே விட்டம் வட்டத்தைச் சந்தித்த புள்ளியையும் இணைத்து ஒரு கோடு வரைக. இதுவே ஒழுங்கு ஐங்கோணத்தின் முதல் பக்கம்.
- இப்பக்கத்தின் மறுமுனை வழியே மீண்டுமொரு விட்டம் வரைந்து மறுபடியும் முன்போல தொடர, ஒழுங்கு ஐங்கோணத்தின் இரண்டாவது பக்கம் கிடைக்கும். இதேபோல் மற்ற பக்கங்களை வரைய ஒழுங்கு ஐங்கோணம் முழுமையாகக் கிடைக்கும்.
மாற்று முறை[தொகு]

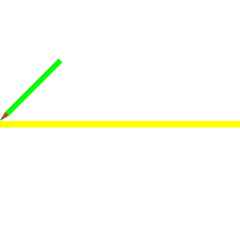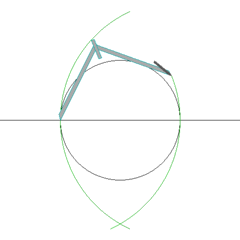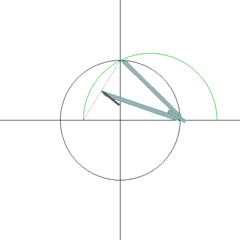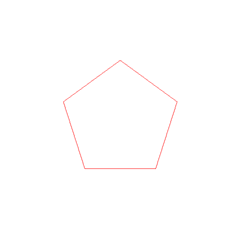
- ஒரு வட்டம் வரைக. (பச்சை நிறம்) இந்த வட்டத்தின் மையம் O.
- வட்டத்தின் மீது ஒரு புள்ளி A குறிக்கவும். இப்புள்ளி நாம் வரையப்போகும் ஐங்கோணத்தின் ஒரு உச்சிப் புள்ளியாக இருக்கும். O மற்றும் A இரண்டையும் இணைக்கவும்.
- OA -க்குச் செங்குத்தாக O வழியே ஒரு கோடு வரைக. இச்செங்குத்துக்கோடு வட்டத்தை ஒரு பக்கத்தில் சந்திக்கும் புள்ளியை B எனக் குறிக்கவும்.
- OB -ன் நடுப்புள்ளி C.
- C -ஐ மையமாகக் கொண்டு A வழியே ஒரு வட்டம் வரைக. இவ்வட்டம் கோடு OB -ஐ மூல வட்டத்துக்குள் (பச்சை நிறம்) சந்திக்கும் புள்ளி D.
- A -ஐ மையமாகக் கொண்டு D வழியே ஒரு வட்டம் வரைக. இந்த வட்டம் மூல வட்டத்தை (பச்சை நிறம்) சந்திக்கும் புள்ளிகள் E மற்றும் F.
- E -ஐ மையமாகக் கொண்டு A வழியே ஒரு வட்டம் வரைக. இந்த வட்டம் மூல வட்டத்தை (பச்சை நிறம்) சந்திக்கும் புள்ளி G.
- F -ஐ மையமாகக் கொண்டு A வழியே ஒரு வட்டம் வரைக. இந்த வட்டம் மூல வட்டத்தை (பச்சை நிறம்) சந்திக்கும் புள்ளிகள் H.
- ஐங்கோணம் AEGHF -ஐ வரைக.
கார்லைல் வட்டங்கள்[தொகு]

கார்லைல் வட்டமானது ஒரு இருபடிச் சமன்பாட்டின் மூலங்களை வடிவவியல் முறையில் காண்பதற்காகக் கண்டுபிடிக்கப்பட்டது.[3] இந்த கண்டுபிடிப்பு ஒரு ஒழுங்கு ஐங்கோணம் வரையும் முறையைக் காணும் வழியைத் தருகிறது.[4]
- ஒரு வட்டம் வரைந்து அதன் மையம் O -ஐக் குறிக்கவும்.
- வட்ட மையப்புள்ளியின் வழியே ஒரு கிடைமட்டக் கோடு வரைக. இக்கோடு வட்டத்தைச் சந்திக்கும் ஒரு புள்ளி B.
- வட்ட மையத்தின் வழியே ஒரு குத்துக்கோடு வரைக. இக்கோடு வட்டத்தைச் சந்திக்கும் ஒரு புள்ளி A.
- OB -ன் மையப்புள்ளி M .
- M -ஐ மையமாகக் கொண்டு A வழியே வரையப்படும் வட்டமானது கிடைமட்டக்கோட்டை மூல வட்டத்துக்குள்ளும் வெளியேயும் சந்திக்கும் புள்ளிகள் முறையே W , V.
- OA -ஐ ஆரமாகவும் W -ஐ மையமாகவும் கொண்டு ஒரு வட்டம் வரைக. இவ்வட்டம் மூல வட்டத்தைச் சந்திக்கும் இரு புள்ளிகளும் ஒழுங்கு ஐங்கோணத்தின் இரு உச்சிப் புள்ளிகளாக இருக்கும்.
- OA -ஐ ஆரமாகவும் V -ஐ மையமாகவும் கொண்டு ஒரு வட்டம் வரைக. இவ்வட்டம் மூல வட்டத்தைச் சந்திக்கும் இரு புள்ளிகளும் ஒழுங்கு ஐங்கோணத்தின் இரு உச்சிப் புள்ளிகளாக இருக்கும்.
- கிடைமட்டக்கோடு மூல வட்டத்தைச் சந்திக்கும் புள்ளி ஐங்கோணத்தின் ஐந்தாவது உச்சிப் புள்ளியாகும்
எளிய முறைகள்[தொகு]

- ஒரு காகிதப் பட்டையில் நுனி முடிச்சொன்று போட்டுக் கொண்டு, பட்டையின் நுனிகளை இழுத்து முடிச்சை தட்டையாக்கி ஒழுங்கு ஐங்கோணத்தை உருவாக்க முடியும். பட்டையின் ஒரு நுனியைப் பின்னோக்கி ஐங்கோணத்தின் மீது மடித்தால் பின்னொளிர்வில் அது ஒரு ஐமுனை விண்மீன் வடிவத்தைத் தரும்.
- ஒரு அட்டையில் ஒழுங்கு அறுகோணம் வரைந்து கொள்ள வேண்டும். எதிர் முனைகளை இணைக்கும் மூன்று மூலைவிட்டங்களில் மடிப்புகள் ஏற்படுத்த வேண்டும். ஒரு சமபக்க முக்கோண மடிப்புத்துண்டு கிடைக்குமாறு,ஒரு முனையிலிருந்து மையம் வரை வெட்டிக்கொள்ள வேண்டும். இவ்வாறு கிடைக்கும் சமபக்க முக்கோண மடிப்புத் துண்டுகளைக் கொண்டு மடித்து ஒரு பிரமிடை உருவாக்கலாம். இப்பிரமிடின் அடிப்பாகம் ஒரு ஒழுங்கு ஐங்கோணமாக இருக்கும்.
இயற்கையில் காணப்படும் ஐங்கோணங்கள்[தொகு]
தாவரங்கள்[தொகு]
-
வெண்டையின் ஐங்கோண வெட்டுமுகம்.
-
மார்னிங் குளோரி -ஐங்கோண வடிவங்கொண்ட மலர்களில் ஒன்று.
-
ஆப்பிளின் சூலகத்தில் சூல்வித்திலை ஐமுனை விண்மீன் வடிவில் உள்ளது.
-
ஐமடி சமச்சீர்மை கொண்ட பழங்களில் ஒன்று நட்சத்திரப்பழம் (விளம்பிப்பழம்).
விலங்குகள்[தொகு]
-
ஒரு நட்சத்திர மீன். பல முள் தோலிகள் ஐமடி சமச்சீர்மை கொண்டுள்ளன.
-
ஒடி நட்சத்திர மீன்களும் ஐங்கோண வடிவ முள் தோலிகள்.
மேற்கோள்கள்[தொகு]
- ↑ George Edward Martin (1998). Geometric constructions. Springer. பக். 6. பன்னாட்டுத் தரப்புத்தக எண்:0387982760. http://books.google.com/books?id=ABLtD3IE_RQC&pg=PA6.
- ↑ The animation is based upon a method described by Herbert W Richmond (1893). "Pentagon". and further discussed in Peter R. Cromwell (1999). Polyhedra. Cambridge University Press. பக். 63. பன்னாட்டுத் தரப்புத்தக எண்:0521664055. http://books.google.com/books?id=OJowej1QWpoC&pg=PA63.
- ↑ Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ). CRC Press. பக். 329. பன்னாட்டுத் தரப்புத்தக எண்:1584883472. http://books.google.com/books?id=Zg1_QZsylysC&pg=PA329.
- ↑ Duane W DeTemple (1991). "Carlyle Circles and the Lemoine Simplicity of Polygon Constructions". The American Mathematical Monthly 98 (2): 97–108. http://apollonius.math.nthu.edu.tw/d1/ne01/jyt/linkjstor/regular/1.pdf. JSTOR link
வெளி இணைப்புகள்[தொகு]
- Weisstein, Eric W., "Pentagon", MathWorld.
- Animated demonstration constructing an inscribed pentagon with compass and straightedge.
- How to construct a regular pentagon with only a only compass and straightedge.
- How to fold a regular pentagon using only a strip of paper
- Definition and properties of the pentagon, with interactive animation
- Renaissance artists' approximate constructions of regular pentagons
- Pentagon. How to calculate various dimensions of regular pentagons.















