பொது மையப் பொருட்கள்
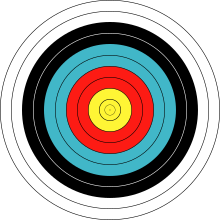

வடிவவியலில் இரண்டு அல்லது இரண்டிற்கும் மேற்பட்ட கணிதப் பொருட்கள் ஒரே மையமுடையவையாக இருந்தால் அவை பொது மையப் பொருட்கள் (concentric objects] என அழைக்கப்படுகின்றன. இதேபோல ஒரே அச்சினை]க் கொண்டவை பொதுவச்சுச் பொருட்கள் (coaxal objects, coaxial objects) எனவும் அழைக்கப்படுகின்றன.
வட்டங்கள்,[1] ஒழுங்கு பல்கோணிகள்[2] ஒழுங்கு பன்முகிகள்,[3] கோளங்கள்[4] ஆகியவை பொதுமையங்கொண்டவையாகவும், உருளைகள்[5] பொதுஅச்சு உடையவையாகவும் அமையலாம்.
வடிவவியல் பண்புகள்[தொகு]
- ஒரு தளத்திலமைந்த இரு பொது மைய வட்டங்களின் ஆரங்கள் வெவ்வேறாக இருக்கும்.[6]
முப்பரிமாணத்தில் அமையும் பொது மைய வட்டங்களின் ஆரங்கள் ஒன்றாக இருக்கலாம். ஆனாலும் அவை வெவ்வேறான வட்டங்களாகும். வானியல் நெடுவரைகளும் புவியின் பெரு வட்டங்களும் இதற்கு எடுத்துக்காட்டுகளாகும்.[7]
- ஆய்லரின் வடிவவியல் தேற்றப்படி, ஒரு முக்கோணத்தின் சுற்றுவட்ட ஆரமானது உள்வட்ட ஆரத்தைப் போல் இருமடங்காக இருந்தால், இருந்தால் மட்டுமே, சுற்றுவட்டமும் உள்வட்டமும் பொது மைய வட்டங்களாக இருக்கும். அந்நிலையில் அம் முக்கோணம், சமபக்க முக்கோணமாக இருக்கும்.[8]:p. 198
- ஒரு ஒழுங்கு n-கோணி, அதன் சுற்றுவட்டம், உள்வட்டம் ஆகிய மூன்றும் பொது மையம் உடையவை.
- ஒழுங்கு பன்முகியுன் உட்கோளம், நடுக்கோளம் [சுற்றுக்கோளம்]] மூன்றும் பொது மையக் கோளங்கள்.
- இரு பொது மைய வட்டங்களுக்கு இடைப்பட்ட பகுதி வட்டவலையம் எனப்படும்.[4]
- குறிப்பிட்ட ஒரு புள்ளியை மையமாகக் கொண்ட வட்டங்களின் தொகுப்பு, வட்டக் கற்றையை உருவாக்கும். இந்த வட்டக் கற்றையில் உள்ள எந்த இரு வட்டகளும் பொது மையமும் வேறுபட்ட ஆரங்களும் உடையவை. வட்டக் கற்றை அமையும் தளத்திலுள்ள புள்ளிகள் (பொது மையம் தவிர) ஒவ்வொன்றும் இக்கற்றையிலுள்ள ஒரேயொரு வட்டத்தில் அமையும். இரு இணைப்பில்லா வட்டங்கள் ஒவ்வொன்றையும், அதிபரவளைய வட்டக் கற்றைகள் ஒவ்வொன்றையும் மோபியசு உருமாற்றத்தின் மூலம் பொது மைய வட்டங்களின் தொகுப்பாக உருமாற்ற முடியும்.[9][10]
பயன்பாடுகளும் எடுத்துக்காட்டுகளும்[தொகு]
நிலையாக இருக்கும் நீரில் சிறு கல்லை எறியும்போது ஏற்படும் சிற்றலைகள் பொதுமைய வட்டங்களாக இருக்கும்.[11] சம இடைவெளியோடு அமைக்கப்பட்ட பொது மைய வட்டங்கள் கொண்ட இலக்கு, குறிபார்த்து எய்தல்/சுடுதல் போன்ற விளையாட்டுகளில் பயன்படுத்தப்படுகின்றன.[12]
ஓரச்சு வடம் பொதுவச்சுடைய ஒரு பயன்பாட்டுப் பொருள்.[13]
கெப்லரின் சூரியக் குடும்பத்தின் மாதிரி, பொது மைய ஒழுங்கு பன்முகிகளையும் கோளங்களையும் கொண்டது.[14]
மேற்கோள்கள்[தொகு]
- ↑ Alexander, Daniel C.; Koeberlein, Geralyn M. (2009), Elementary Geometry for College Students, Cengage Learning, p. 279, ISBN 9781111788599.
- ↑ Hardy, Godfrey Harold (1908), A Course of Pure Mathematics, The University Press, p. 107.
- ↑ Gillard, Robert D. (1987), Comprehensive Coordination Chemistry: Theory & background, Pergamon Press, pp. 137, 139, ISBN 9780080262321.
- ↑ 4.0 4.1 Apostol, Tom (2013), New Horizons in Geometry, Dolciani Mathematical Expositions, vol. 47, Mathematical Association of America, p. 140, ISBN 9780883853542.
- ↑ Spurk, Joseph; Aksel, Nuri (2008), Fluid Mechanics, Springer, p. 174, ISBN 9783540735366.
- ↑ Cole, George M.; Harbin, Andrew L. (2009), Surveyor Reference Manual, www.ppi2pass.com, §2, p. 6, ISBN 9781591261742.
- ↑ Morse, Jedidiah (1812), The American universal geography;: or, A view of the present state of all the kingdoms, states, and colonies in the known world, Volume 1 (6th ed.), Thomas & Andrews, p. 19.
- ↑ Dragutin Svrtan and Darko Veljan (2012), "Non-Euclidean versions of some classical triangle inequalities", forumgeom.fau.edu, Forum Geometricorum, pp. 197–209
- ↑ Hahn, Liang-shin (1994), Complex Numbers and Geometry, MAA Spectrum, Cambridge University Press, p. 142, ISBN 9780883855102.
- ↑ Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (2011), Geometry, Cambridge University Press, pp. 320–321, ISBN 9781139503709.
- ↑ Fleming, Sir John Ambrose (1902), Waves and Ripples in Water, Air, and Æther: Being a Course of Christmas Lectures Delivered at the Royal Institution of Great Britain, Society for Promoting Christian Knowledge, p. 20.
- ↑ Haywood, Kathleen; Lewis, Catherine (2006), Archery: Steps to Success, Human Kinetics, p. xxiii, ISBN 9780736055420.
- ↑ Weik, Martin (1997), Fiber Optics Standard Dictionary, Springer, p. 124, ISBN 9780412122415.
- ↑ Meyer, Walter A. (2006), Geometry and Its Applications (2nd ed.), Academic Press, p. 436, ISBN 9780080478036.
வெளியிணைப்புகள்[தொகு]
- Geometry: Concentric circles demonstration With interactive animation
