உள்வரை கோணம்
வடிவவியலில் உள்வரை கோணம்(inscribed angle) என்பது ஒரு வட்டத்தின் இரு வெட்டுக்கோடுகள்(secants) (ஒரு வெட்டுக்கோடு அல்லது ஒரு தொடுகோடு) வட்டத்தின் மேல் வெட்டிக் கொள்ளும்போது உண்டாகும் கோணமாகும். குறிப்பாக உள்வரை கோணத்தை வட்டத்தின் பொது முனைப்புள்ளியுடைய இரு நாண்களால் வரையறுக்கப்படுவதாகக் கருதலாம்.
ஒரு வட்டத்தின் உள்வரை கோணம் வட்ட மையக்கோணத்தில் பாதி; வட்டத்தின் ஒரு நாணின் வட்டவில்லால் உருவாகும் அனைத்து உள்வரை கோணங்களும் சமம்; ஒரே நாணின் இரு வெவ்வேறு உள்வரை கோணங்களின் கூடுதல் 180° -ஆகிய அடிப்படைப் பண்புகள், யூக்ளிடின் எலிமெண்ட்ஸ்: புத்தகம் 4- ல் விவாதிக்கப்பட்டுள்ளன.
பண்பு[தொகு]
- ஒரு உள்வரை கோணம் வட்டத்தின் மீது ஒரு வில்லை வெட்டுகிறது. உள்வரை கோணத்தின் உட்புறமாக அமையும் வட்டத்தின் பகுதி இந்த வில்லாகும். இந்த வில்லின் அளவு(மையக்கோணத்திற்குச் சமம்) உள்வரை கோணத்தின் அளவில் இரு மடங்காகும்.
இந்தப் பண்பினால் வட்டத்துக்குள் பல விளைவுகள் கிடைக்கின்றன. எடுத்துக்காட்டாக:
- ஒரு வட்டத்தின் இரு நாண்கள் ஒன்றையொன்று வெட்டிக்கொள்ளும்போது ஒரு நாணின் வெட்டுத்துண்டுகளின் நீளங்களின் பெருக்குத் தொகை மற்றொரு நாணின் வெட்டுத்துண்டுகளின் நீளங்களின் பெருக்குத் தொகைக்குச் சமமாக இருக்கும் என்பதை இப்பண்பினைக் கொண்டு நிறுவலாம்.
- இதேபோல் ஒரு வட்ட நாற்கரத்தின் எதிர்கோணங்கள் மிகைநிரப்புக் கோணங்களாக இருக்கும் என்பதையும் இப்பண்பினைப் பயன்படுத்தி நிறுவலாம்.
நிறுவல்[தொகு]
பகுதி-1: விட்டத்தை ஒரு நாணாகக் கொண்ட உள்வரை கோணம்[தொகு]
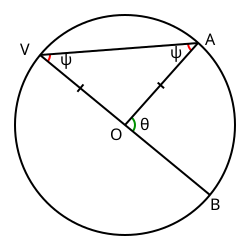
வட்ட மையம் O. V , A -வட்டத்தின் மீது இரு புள்ளிகள். கோடு VO வரைந்து அதனை O -ஐத் தாண்டி வட்டத்தை B -இல் வெட்டுமாறு நீட்ட வேண்டும். இப்புள்ளி V க்கு விட்ட எதிர்முனையாக அமையும். V -ஐ உச்சியாகக் கொண்டு கரங்கள் A , B வழிச் செல்லுமாறு ஒரு உள்வரை கோணத்தை வரைய வேண்டும்.
கோணம் BOA -மையக்கோணம். அதனை θ என்க. கோடு OA வரைக. கோடுகள் OV , OA இரண்டும் வட்டத்தின் ஆரங்கள் என்பதால் சம நீளமுள்ளவை. முக்கோணம் VOA ஒரு இருசமபக்க முக்கோணம். எனவே உள்வரை கோணம் BVA மற்றும் கோணம் VAO இரண்டும் சமம். அவற்றின் அளவை ψ எனக் கொள்ளவும்.
கோணங்கள் BOA , AOV இரண்டும் ஒரே கோட்டின் மீது அமைவதால் மிகைநிரப்புக் கோணங்கள். அவற்றின் கூடுதல் 180°. ஃ கோணம் AOV -இன் அளவு 180° − θ.
முக்கோணம் VOA -இன் மூன்று கோணங்கள்:
- 180° − θ
- ψ
- ψ.
ஒரு முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180° என்பதால்
இருபுறமும் 180° கழிக்க:
இங்கு θ என்பது வில் AB -ஐத் தாங்கும் வட்ட மையக்கோணம். ψ என்பது வில் AB -ஐத் தாங்கும் உள்வரை கோணம்.
பகுதி-2: வட்ட மையத்தை உட்புறமாகக் கொண்ட உள்வரை கோணங்கள்[தொகு]

O வட்ட மையம். V, C, D வட்டத்தின் மீது அமையும் மூன்று புள்ளிகள். கோடுகள் VC , VD வரைய, கோணம் DVC உள்வரை கோணமாகும். கோடு VO வரைந்து அதனை O -ஐத் தாண்டி அது வட்டத்தை E -ல் வெட்டும்படி நீட்டிக்க வேண்டும். கோணம் DVC வட்டத்தின்மீது வில் DC -ஐத் தாங்குகிறது.
E , புள்ளி V.-இன் விட்ட எதிர்முனையாகும். கோணங்கள் DVE , EVC இரண்டும் உள்வரை கோணங்கள். இவ்விரு உள்வரை கோணங்களின் ஒரு பக்கம் விட்டமாக இருப்பதால் பகுதி 1 -இன் முடிவை பயன்படுத்தலாம்.
மேலும்
- என்க.
கோடுகள் OC , OD வரைக. கோணம் DOC ஒரு மையக்கோணம். அதேபோல் கோணங்கள் DOE , EOC இரண்டும் மையக்கோணங்கள்.
- என்க.
எனவே
பகுதி 1 முடிவின்படி
- , .
இதைச் சமன்பாடு (2) இல் பயன்படுத்த,
ஃ சமன்பாடு (1) -இன்படி
பகுதி-3: வட்ட மையத்தை வெளிப்புறத்தில் கொண்ட உள்வரை கோணங்கள்[தொகு]

O வட்ட மையம். V, C, D மூன்றும் வட்டத்தின் மீது அமையும் புள்ளிகள். கோடுகள் VC , VD வரைய கோணம் DVC ஒரு உள்வரை கோணம். கோடு VO வரைந்து அதனை O -ஐத் தாண்டி அது வட்டத்தை E புள்ளியில் வெட்டுமாறு நீட்டிக்க வேண்டும். கோணம் DVC வட்டத்தின் மீது வில் DC ஐத் தாங்குகிறது.
E, புள்ளி V -ன் விட்ட எதிர்முனை. கோணங்கள் DVE , EVC இரண்டும் உள்வரை கோணங்கள். இக்கோணங்களின் ஒரு பக்கம் விட்டமாக அமைவதால் இக்கோணங்களுக்குப் பகுதி 1 முடிவினைப் பயன்படுத்தலாம்.
- .
- என்க.
எனவே,
கோடுகள் OC , OD வரைக. கோணம் DOC மையக்கோணம். இதேபோல் கோணங்கள் DOE , EOC இரண்டும் மையக்கோணங்கள்.
- என்க.
பகுதி 1 -இன்படி
- .
இந்த முடிவுகளை சமன்பாடு (4) -இல் பயன்படுத்த
எனவே சமன்பாடு (3) -இன்படி,
உள்வரை கோணத் தேற்றம்[தொகு]

உள்வரை கோணத் தேற்றம்:
- ஒரு வட்டத்துக்குள் வரையப்பட்ட ஒரு உள்வரை கோணத்தின் அளவு θ , அந்த உட்கோணம் வட்டத்தில் வெட்டும் அதே வில்லைத் தாங்கும் மையக்கோணம் 2θ -இன் அளவில் பாதியாக இருக்கும். எனவே உட்கோணத்தின் உச்சி நகர்ந்து வட்டத்தின் மீதே வெவ்வேறு நிலைகளுக்கு இடம் மாறினாலும் உட்கோணத்தின் அளவு மாறாது.
இதுவே உள்வரை கோணத் தேற்றத்தின் கூற்றாகும்.
பல யூக்ளிடின் தள வடிவவியல் நிறுவல்களில் இத்தேற்றம் பயன்படுத்தப்பட்டுள்ளது. இத்தேற்றத்தின் ஒரு சிறப்பு வகை தேலேசுத் தேற்றமாகும். தேலேசுத் தேற்றப்படி ஒரு வட்டத்தில் அதன் விட்டம் தாங்கும் கோணம் செங்கோணமாகும். இதிலிருந்து ஒரு வட்ட நாற்கரத்தின் எதிர்கோணங்களின் கூடுதல் 180° ஆகும் என்றியலாம். இதற்கு மறுதலையாக எதிர்கோணங்களின் கூடுதல் 180° கொண்ட நாற்கரத்தை ஒரு வட்டத்துக்குள் வரையலாம் என்பதும் உண்மையாகும்.
நிறுவல்[தொகு]
- உள்வரை கோணத்தின் ஒரு பக்கம் வட்டத்தின் விட்டமெனில் பகுதி1 -இன் படி நிறுவலாம்.
- பிற உட்கோணங்களுக்கு அவற்றின் உச்சியிலிருந்து ஒரு விட்டம் வரைந்தால் விட்டத்தை ஒரு பக்கமாகக் கொண்ட இரு உட்கோணங்கள் கிடைக்கும். இவற்றுக்கு முன்போலவே பகுதி 1 -இன்படி நிறுவி இரண்டின் அளவுகளைக் கூட்டி நாம் முதலில் எடுத்துக்கொண்ட உட்கோணத்தின் அளவைப் பெறலாம்.
- மஞ்சள் நிற உட்கோணத்தின் மையக்கோணத்தின் அளவு 360°-2θ. எனவே அதன் அளவு 180°-θ.
கிளை முடிவுகள்[தொகு]
வட்டத்தின் ஒரு நாணும் ஒரு தொடுகோடும் வெட்டுமிடத்தில் உண்டாகும் கோணத்தின் அளவு அந்நாணின் மையக்கோணத்தின் அளவில் பாதியாக இருக்கும்.
மேற்கோள்கள்[தொகு]
- Ogilvy CS (1990). Excursions in Geometry. Dover. பக். 17–23. பன்னாட்டுத் தரப்புத்தக எண்:0-486-26530-7. https://archive.org/details/excursionsingeom0000ogil_w9f7
- Gellert W, Küstner H, Hellwich M, Kästner H (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. பக். 172. பன்னாட்டுத் தரப்புத்தக எண்:0-442-22646-2. https://archive.org/details/vnrconciseencycl0000unse_u7k9.
வெளி இணைப்புகள்[தொகு]
- Weisstein, Eric W., "Inscribed Angle", MathWorld.
- Relationship Between Central Angle and Inscribed Angle பரணிடப்பட்டது 2012-09-09 at the வந்தவழி இயந்திரம்
- Munching on Inscribed Angles at cut-the-knot
- Arc Central Angle பரணிடப்பட்டது 2006-10-30 at the வந்தவழி இயந்திரம் With interactive animation
- Arc Peripheral (inscribed) Angle With interactive animation
- Arc Central Angle Theorem With interactive animation






















