கோண அதிர்வெண்

கோண அதிர்வெண் ω (நொடிக்கான ரேடியன்கள்), அதிர்வெண் ν ஐ (நொடிக்கான சுழற்சிகள், பொதுவாக ஹேட்சில் அளக்கப்படுகிறது) விட 2π எனும் காரணியால் பெரியது. இப்படத்தில் அதிர்வெண்ணைக் குறிக்க f அல்லாது ν பயன்படுத்தப்படுகிறது.

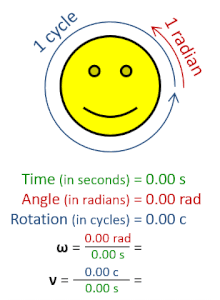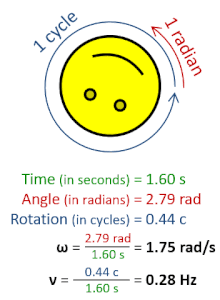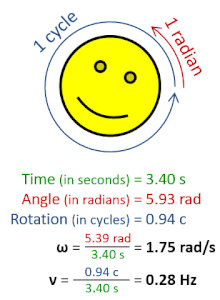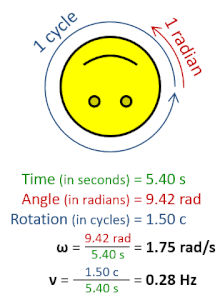
இயற்பியலில் கோண அதிர்வெண் எனப்படுவது சுழலும் விகிதத்தை அளவிடும் எண்ணிக்கணியம். கோண அதிர்வெண்ணானது கோண வேகம் எனப்படும் திசையன் கணியத்தின் பருமன் ஆகும். கோண அதிர்வெண் திசையன் ${\vec {\omega }}$ எனப்படுவது சிலவேளைகளில் கோண வேகத்திற்கு ஒத்தசொல்லாக பயன்படுகிறது.

ஓர் சுழற்சி 2π ரேடியன்களிற்கு சமனாகும், எனவே

$\omega ={{2\pi } \over T}={2\pi f},$

இங்கு

ω என்பது கோண அதிர்வெண் அல்லது கோணக் கதி (செக்கனிற்கான ரேடியன்களில் அளக்கப்படும்),

T என்பது சுழற்சிக்காலம் (நொடிகளில் அளக்கப்படும்),

f என்பது அதிர்வெண் (ஹேட்சில் அளக்கப்படும்),

அலகுகள்

SI அலகுகளில் கோண அதிர்வெண் நொடிக்கான ரேடியன்கள் எனப்படுகிறது, பரிமாணப்படி அலகு ஹேட்சு என்பதும் சரியானதே, ஆனால் நடைமுறையில் சாதாரண அதிர்வெண் f இற்கே பாவிக்கப்படுகிறது, ω இற்கு இல்லையென்றே கூறலாம், இந்த நடைமுறையால் குழப்பம் தவிர்க்கப்படுகிறது.

எடுத்துக்காட்டுகள்

ஓர் கோளம் அச்சுப்பற்றி சுழல்கிறது, அச்சிலிருந்து தொலைவில் அமைந்த புள்ளிகள் விரைவாக நகர்கின்றன இது ω=v/r இனை திருப்திப்படுத்துகிறது.

வட்ட இயக்கம்

வட்ட இயக்கத்திலுள்ள பொருளின் அச்சிலிருந்தான தூரம், தொடலி வேகம், கோண அதிர்வெண் ஆகியவற்றிற்கிடையில் தொடர்புண்டு:

$\omega =v/r$

சுருளிவில்லின் அலைவு

மரபார்ந்த விசையியல்

${\vec {F}}={\frac {\mathrm {d} }{\mathrm {d} t}}(m{\vec {v}})$ நியூட்டனின் இரண்டாவது விதி

வரலாறு · காலக்கோடு அடிப்படைக் கருத்துக்கள் வெளி · நேரம் · திணிவு · விசை ஆற்றல் · உந்தம் யாப்புகள் நியூட்டனின் பொறியியல் லாக்ராஞ்சி விசையியல் Hamiltonian mechanics பிரிவுகள் நிலையியல் இயக்கவியல் இயங்கியல் பயன்பாட்டு விசையியல் வான விசையியல் தொடர்ம விசையியல் புள்ளிவிவர இயக்கவியல் அறிவியலாளர்கள் கலீலியோ · கெப்லர் · நியூட்டன் இலப்லாசு · Hamilton · டெ'ஆலம்பர்ட் Cauchy · லாக்ராஞ்சி · ஆய்லர்

சுருளிவில்லில் இணைக்கப்பட்ட பொருள் ஆடலுறும். சுருளிவில்லை திணிவற்றதாகவும் தடையில்லாததாகவும் கருதினால் அதன் இயக்கம் பின்வரும் கோண அதிர்வெண்ணுடைய எளிய இசையியக்கமாக இருக்கும்:

$\omega ={\sqrt {\frac {k}{m}}},$

இங்கு

k வில் மாறிலி

m பொருளின் திணிவு.

ω என்பது இயற்கை அதிர்வெண் (இது சிலவேளைகளில் ω₀ ஆல் குறிக்கப்படும்).

அலைவுறும் பொருளின் அதிர்வெண்

$a=-\omega ^{2}x\;,$ இனால் கணிக்கப்படும்,

இங்கு x சமனிலைத் தானத்திலிருந்தான இடப்பெயர்ச்சி.

இங்கு சாதாரண அதிர்வெண்ணைப் பயன்படுத்துகையில் இச்சமன்படானது கீழ்வருமாறு அமையும்

$a=-4\pi ^{2}f^{2}x\;.$

LC மின்சுற்றுக்கள்

LC சுற்றின் பரிவு அதிர்வெண்ணானது மின் கொள்ளளவம் (C ஃபரட்டில் அளக்கப்படுகிறது), மின் தூண்டுதிறன் (L ஹென்றியில் அளக்கப்படுகிறது) ஆகியவற்றின் பெருக்கத்தின் தலைகீழின் வர்க்கமூலத்திற்கு சமனாகும்.

$\omega ={\sqrt {1 \over LC}}$

மேலும் பார்க்க

• எளிய இசை இயக்கம்

மேற்கோளும் குறிப்புகளும்

தொடர்புடைய வாசிப்பிற்கு:

• Olenick ,, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007). The Mechanical Universe. New York City: Cambridge University Press. பக். 383–385, 391–395. பன்னாட்டுத் தரப்புத்தக எண்:978-0-521-71592-8. http://books.google.com/?id=xMWwTpn53KsC&pg=RA1-PA383&dq=angular+frequency.