அதிபரவளைவு

கணிதவியலில் அதிபரவளைவு (Hyperbola) என்பது, ஒருவகைக் கூம்பு வெட்டு ஆகும். இது ஒரு இரட்டை நேர்வட்டக் கூம்பின் இரு பாதிகளையும் ஒரு தளம் வெட்டும்போது கிடைக்கும் வெட்டுமுகமாகும். பரவளையம் மற்றும் நீள்வட்டம் காண்பதற்கு ஓர் தளத்தால் இரட்டைக் கூம்பின் ஒரு பாதியை மட்டும் வெட்டினால் போதும்.
நிலையான இரண்டு புள்ளிகளிலிருந்து உள்ள தூரங்களின் வித்தியாசத்தின் தனிமதிப்பு மாறிலியாக உள்ளவாறு இயங்கும் புள்ளியின் ஒழுக்கு அதிபரவளைவு ஆகும் எனவும் இதற்கு வரைவிலக்கணம் கூறலாம். மேற்குறித்த நிலையான புள்ளிகள் இரண்டும் அதிபரவளைவின் குவியங்கள் எனப்படும். முன்னர் குறிப்பிட்ட நிலையான தூர வித்தியாசம், அதிபரவளைவின் மையத்துக்கும், அதன் உச்சியொன்றுக்கும் இடையிலான தூரத்தின் (a) இரண்டு மடங்கு (2a) ஆகும்.
தளத்தில் ஒரு நிலையான புள்ளியிலிருந்து (குவியம்) உள்ள தூரம் மற்றும் ஒரு நிலையானக் கோட்டிலிருந்து (இயக்குவரை) அமையும் தூரம் இவை இரண்டின் விகிதம் மாறிலியாகவும் அம்மாறிலியின் மதிப்பு 1 -ஐ விட அதிகமானதாகவும் உள்ளவாறு நகரும் புள்ளியின் இயங்குவரையாகவும் அதிபரவளைவு வரையறுக்கப்படுகிறது.
அதிபரவளைவின் ஆங்கிலப் பெயரான "hyperbola" மிகுதியான என்ற பொருள் கொண்ட ὑπερβολή -கிரேக்கச் சொல்லில் இருந்து உருவானது. கிரேக்க கணிதவியலாளர் அப்பலோனியசால் (கிமு 262 - கிமு 190) கூம்பு வெட்டுக்களைப் பற்றிய அவரது படைப்பான (Conics) இல் இப்பெயர் பயன்படுத்தப்பட்டதாகக் கருத்து நிலவுகிறது.
அதிபரவளையம் காட்டீசியன் தளத்தில்
என்னும் சமன்பாட்டினால் குறிக்கப்படும் ஒரு வளைவரை ஆகும். இங்கே ஆக உள்ளதுடன் எல்லாக் குணகங்களும் மெய்யெண்களாகும்.
அதிபரவளைவின் கூறுகள்[தொகு]
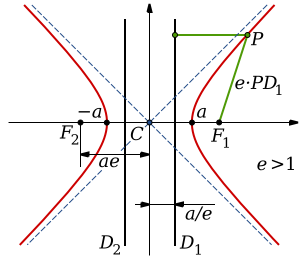
பரவளைவைப் போன்று அதிபரவளையமும் திறந்த வளைவரையாகும். அதிபரவளைவின் வளைவரை பிரிக்கப்பட்ட சமச்சீரான இரு கிளைப்பகுதிகள் உடையது.
உச்சி
இரு கிளைப் பகுதிகளின் மீது ஒன்றுக்கொன்று மிகக்குறைந்த தூரத்தில் உள்ள புள்ளிகள் இரண்டு அதிபரவளைவின் உச்சிகள் எனப்படும். இரு உச்சிகளுக்கும் இடையே உள்ள தூரம் 2a எனக் குறிப்பிடப்படுதல் வழமை.
மையம்
இரு உச்சிகளின் நடுப்புள்ளி அதிபரவளையத்தின் மையம். இது அதிபரவளையத்தின் இரு அச்சுகளும் சந்திக்கும் புள்ளியாக அமையும்.
அச்சு
அதிபரவளைவிற்கு குறுக்கு அச்சு, துணை அச்சு என இரு அச்சுகள் உள்ளன. அதிபரவளைவின் உச்சிகள் இரண்டையும் இணைக்கும் கோட்டுத்துண்டு குறுக்கச்சாகும். குறுக்கச்சுக்குச் செங்குத்தாக அதிபரவளையத்தின் மையத்தின் வழிச் செல்லும் கோட்டுத்துண்டு துணையச்சாகும். குறுக்கச்சின் நீளம் 2a மற்றும் துணையச்சின் நீளம் 2b (b2 = a2(e2 - 1) எனவும் கொள்ளப்படுகிறது. அதிபரவளையத்தின் வளைவரை குறுக்கச்சு மற்றும் துணையச்சு இரண்டைப் பொறுத்தும் பிரதிபலிப்புச் சமச்சீருடன் அமையும்.
குவியம் தளத்தில் அமையும் ஒரு நிலையான புள்ளியிலிருந்து உள்ள தூரம் மற்றும் ஒரு நிலையான கோட்டிலிருந்து அமையும் தூரம் இவை இரண்டின் விகிதம் எப்பொழுதும் மாறிலியாக உள்ளவாறு இயங்கும் புள்ளியின் இயங்குவரையாக அதிபரவளையம் வரையறுக்கப்படுவதில்,
இந்த நிலையான புள்ளி அதிபரவளையத்தின் குவியம் எனப்படும். சமச்சீர்த்தன்மையால் அதிபரவளையத்திற்கு இரு குவியங்கள் உள்ளன. இவை அதிபரவளைவின் மையத்திலிருந்து சமதூரத்தில், குறுக்கச்சின் மீது, உச்சிகளின் மறுபக்கங்களில் அமைந்த இரு புள்ளிகளாகும். இவை F1 மற்றும் F2 எனக் குறிக்கப்படுகின்றன.
அதிபரவளைவின் மீதமையும் ஏதேனும் ஒரு புள்ளிக்கும் இவ்விரு குவியங்களுக்கும் இடைப்பட்ட தூரங்களின் வித்தியாசம் மாறிலியாகவும் அம்மாறிலி குறுக்கச்சின் நீளத்திற்குச் சமமானதாகவும் இருக்கும்.
.
இயக்குவரை
மேலே குவியத்தில் கூறப்பட்டுள்ள வரையறையின் நிலையான கோடு அதிபரவளையத்தின் இயக்குவரை எனப்படும். அதிபரவளையத்தின் சமச்சீர்ப் பண்பால் அதற்கு இரண்டு இயக்குவரைகள் உள்ளன. இவை இரண்டும் அதிபரவளையத்தின் துணை அச்சுக்குக்கு இணையாக இருபுறமும் மையத்திலிருந்து சமதூரத்தில் அமைகின்றன. அதிபரவளையத்தின் மையத்திற்கும் இயக்குவரைக்கும் இடைப்பட்ட தூரம் a/e.
வட்ட விலகல்
மேலே குவியத்தில் கூறப்பட்டுள்ள வரையறையின் மாறிலி அதிபரவளையத்தின் வட்டவிலகல் எனப்படும். இதன் மதிப்பு எப்பொழுதும் ஒன்றைவிட அதிகமானதாக இருக்கும்.
வட்ட விலகலின் குறியீடு: e அல்லது
- (f, அதிபரவளையத்தின் உச்சிக்கும் அதற்குரிய குவியத்திற்கும் இடைப்பட்ட தூரம்.)
செவ்வகலம்
அதிபரவளையத்தின் குவியங்களின் வழியாக அதன் இயக்குவரைகளுக்கு இணையாக வரையப்பட்ட நாண் அதிபரவளையத்தின் செவ்வகலம் (latus rectum) எனப்படும். செவ்வகலத்தில் பாதி அரைச் செவ்வகலம் எனப்படும்.
அணுகுகோடுகள்
மையத்திலிருந்து தூரமாகச் செல்லச் செல்ல அதிபரவளையமானது அதன் மையத்தில் வெட்டிக்கொள்ளும் இரு கோடுகளை நோக்கி அணுகிக் கொண்டே செல்கிறது. அக்கோடுகள் அதிபரவளையத்தின் அணுகுகோடுகள் என அழைக்கப்படுகின்றன. மையத்திலிருந்து தூரம் அதிகரிக்க அதிகரிக்க அதிபரவளையத்திற்கும் அணுகுகோடுகளுக்கும் இடையேயுள்ள தூரம் கணிசமாகக் குறைந்து கொண்டேயிருக்கிறது. ஆனால் அதிபரவளையம் அணுகுகோடுகளை ஒருபோதும் சந்திப்பதில்லை.
அதிபரவளையத்தின் குறுக்கச்சை கார்ட்டீசியன் ஆள்கூற்று முறைமையின் x-அச்சின் மீது எடுத்துக் கொண்டால் அணுகுகோடுகளின் சாய்வுகள் அளவில் சமமாகவும் குறியில் எதிரானதாகவும் இருக்கும்:
குறுக்கச்சுக்கும் அணுகுகோட்டிற்கும் இடைப்பட்ட கோணம் θ எனில்:
சமன்பாடுகள்[தொகு]
பொதுவடிவம்[தொகு]
(x, y) இல் அமைந்த பொதுவடிவ இருபடிச் சமன்பாடு கீழ்க்கண்ட கட்டுப்பாட்டுக்கு உட்பட்டு ஒரு அதிபரவளையத்தைக் குறிக்கும்.
கட்டுப்பாடு:
- ஆக உள்ளதுடன் எல்லாக் குணகங்களும் மெய்யெண்களாகும்.
நியமன வடிவம்[தொகு]
ஆதியை மையமாகவும் x மற்றும் y அச்சுகளை முறையே குறுக்கு அச்சு மற்றும் துணை அச்சாகக் கொண்ட அதிபரவளையத்தின் கார்ட்டீசியன் ச்மன்பாடு:
- மற்றும்
இந்த அதிபரவளையத்தின்
- மையம்:(0,0)
- குறுக்கு அச்சு --அச்சு
- துணையச்சு --அச்சு
- குறுக்கச்சின் நீளம் =2a
- துணை அச்சின் நீளம் =2b
- குவியங்கள்: மற்றும்
- இயக்குவரைகளின் சமன்பாடுகள்:
- வட்டவிலகல்:
- செவ்வகலத்தின் நீளம் =
அதிபரவளைங்களின் வகைகள்[தொகு]
கிழக்கு-மேற்கு நோக்கித் திறந்த அதிபரவளையம்[தொகு]
குறுக்கச்சு கார்ட்டீசியன் ஆள்கூற்று முறைமையின் x-அச்சுடனும் மையம் ஆதிப்புள்ளியுடனும் பொருந்தும் அதிபரவளைவின் சமன்பாடு:
இந்த அதிபரவளையம் கிழக்கு-மேற்கு நோக்கித் திறந்த அதிபரவளையம் என அழைக்கப்படும்.
வடக்கு-தெற்கு நோக்கித் திறந்த அதிபரவளையம்[தொகு]
குறுக்கச்சு கார்ட்டீசியன் ஆள்கூற்று முறைமையின் y-அச்சுடனும் மையம் ஆதிப்புள்ளியுடனும் பொருந்தும் அதிபரவளைவின் சமன்பாடு:
இந்த அதிபரவளையம் வடக்கு-தெற்கு நோக்கித் திறந்த அதிபரவளையம் என அழைக்கப்படும்.
கிழக்கு-மேற்கு நோக்கித் திறந்த, ஆதியை மையமாக உடைய அதிபரவளையத்திற்குச் சர்வசமமாக, அதே வட்டவிலகல்கள் கொண்டு அமையும் அதிபரவளையங்கள் வடக்கு-தெற்கு நோக்கித் திறந்த ஆதியை மையமாக உடைய அதிபரவளையத்திற்கும் சர்வசமமாக அமையும் (இங்கும் வட்டவிலகல்கள் சமமாக இருக்கும்). தேவையான சுழற்சியால் திறப்பு திசையை மாற்றக் கொள்ளலாம், மேலும் இடப்பெயர்ச்சியால் மையங்களை ஆதிக்கு நகர்த்தலாம் என்பதால் இது சாத்தியமாகிறது. வழக்கமாக கிழக்கு-மேற்கு நோக்கித் திறந்த அதிபரவளையங்களே ஆய்வுக்குப் பயன்படுத்தப்படுகிறது.
துணை அதிபரவளையம்[தொகு]
ஒவ்வொரு அதிபரவளையத்துக்கும் ஒரு துணை அதிபரவளையம் உண்டு. ஒரு அதிபரவளையத்தின் குறுக்கச்சு மற்றும் துணையச்சு இரண்டையும் பரிமாற்றம் செய்யக் கிடைக்கும் புது அதிபரவளையம் எடுத்துக்கொண்ட அதிபரவளையத்தின் துணை அதிபரவளையம் எனப்படும்.
அதிபரவளையத்தின் சமன்பாடு:
- எனில்:
துணை அதிபரவளையத்தின் சமன்பாடு:
- .
துணை அதிபரவளையத்தின் வரைபடத்தை 90° சுழற்றினால் கிடைக்கக்கூடிய புது அதிபரவளையத்தின் சமன்பாடு, a மற்றும் b இரண்டும் இடம் மாறியிருக்கும் மாற்றத்தைத் தவிர, எடுத்துக் கொண்ட அதிபரவளையத்தின் சமன்பாட்டினைப் போலவே அமையும். அதிபரவளையம் மற்றும் துணை அதிபரவளையத்தின் கோணங்கள் நிரப்புக் கோணங்களாக அமையும். அதனால் அதிபரவளையத்தின் கோணம் θ = 45° (செவ்வக அதிபரவளையம்) கொண்ட அதிபரவளையத்துக்கு மட்டும் அதிபரவளையம் மற்றும் துணை அதிபரவளையம் இரண்டின் வட்டவிலகலும் சமமாக இருக்கும். பிற அதிபரவளையங்களுக்கு அதிபரவளையம் மற்றும் துணை அதிபரவளையம் இரண்டின் வட்டவிலகல்கள் வெவ்வேறாக இருக்கும். எனவே 90° சுழற்சியால் துணை அதிபரவளையத்தை மூல அதிபரவளையத்தோடு பொருத்த முடியாது.
செவ்வக அதிபரவளையம்[தொகு]

ஒரு அதிபரவளையத்தின் குறுக்கச்சின் நீளமும் துணையச்சின் நீளமும் சமம் (b = a) எனில், அதன் அணுகு கோடுகளுக்கு இடைப்பட்ட கோணம் 2θ = 90°. இத்தகைய அதிபரவளையம் செவ்வக அதிபரவளையம் எனப்படும்.
ஆதியை மையமாகவும் ஆய அச்சுக்களை அணுகுகோடுகளாகவும் கொண்ட செவ்வக அதிபரவளையத்தின் கார்ட்டீசியன் சமன்பாடு:
- இங்கு
பிற பண்புகள்[தொகு]
- ஒரு கோடு அதிபரவளையத்தின் ஒருகிளையை M மற்றும் N புள்ளிகளிலும் அணுகுகோடுகளை P மற்றும் Q புள்ளிகளிலும் சந்தித்தால், கோட்டுத்துண்டுகள் MN மற்றும் PQ ஆகிய இரண்டின் நடுப்புள்ளிகளும் ஒன்றாக இருக்கும்.[1][2]:p.49,ex.7
- பின்வருபவை ஒரு புள்ளியில் சந்திக்கும்:
- அதிபரவளையத்தின் மையத்தை மையமாகக் கொண்டு அதிபரவளையத்தின் குவியங்களின் வழிச் செல்லும் வட்டம்;
- அதிபரவளையத்தின் ஏதாவது ஒரு உச்சியில் அதிபரவளையத்துக்கு வரையப்படும் தொடுகோடு;
- அதிபரவளையத்தின் ஏதாவது ஒரு அணுகுகோடு.[1][3]
- மேலும் கீழே தரப்பட்டுள்ளவை ஒரு புள்ளியில் சந்திக்கும்.
- அதிபரவளையத்தின் மையத்தை மையமாகக் கொண்டு அதிபரவளையத்தின் உச்சிகளின் வழிச் செல்லும் வட்டம்;
- அதிபரவளையத்தின் ஏதாவது ஒரு இயக்குவரை;
- அதிபரவளையத்தின் ஏதாவது ஒரு அணுகுகோடு.[3]
- அதிபரவளையத்தின் மீது அமையும் ஒரு புள்ளி P இலிருந்து ஒரு அணுகு கோட்டிற்கு, மற்றொரு அணுகு கோட்டிற்கு இணையான கோட்டின் வழியே அமையும் செங்குத்து தூரம் மற்றும் இரண்டாவது அணுகு கோட்டிற்கு முதல் அணுகு கோட்டிற்கு இணையான கோட்டின் வழியே அமையும் செங்குத்து தூரம் ஆகிய இவை இரண்டின் பெருக்குத் தொகை, புள்ளி P அதிபரவளையத்தின் மேல் அமையும் இடத்தைச் சார்ந்ததல்ல.[3]
- அதிபரவளையத்தின் மீது அமையும் ஒரு புள்ளியிலிருந்து அதன் இரு உச்சிகளுக்கு வரையப்படும் கோடுகளின் சாய்வுகளின் பெருக்குத்தொகை அப்புள்ளி அதிபரவளையத்தின் மீது அமையும் இடத்தைச் சார்ந்ததல்ல.[4]
- அதிபரவளையத்தின் ஒரு தொடுகோடு தொடுகோட்டிற்கும் அதன் இரு அணுகுகோடுகளுக்கும் இடைப்பட்ட கோட்டுத்துண்டின் நடுப்புள்ளியாகத் தொடுகோட்டின் தொடுபுள்ளி அமையும்.[2]:p.49,ex.6[4][5]
- அதிபரவளையத்தின் ஒரு தொடுகோடு மற்றும் அதன் இரு அணுகுகோடுகளால் அடைபடும் முக்கோணத்தின் பரப்பு தொடுபுள்ளி அமையும் இடத்தைச் சார்ந்ததல்ல.[2]:p.49,ex.6 இம்முக்கோணத்தின் பரப்பு ab (a அரைக் குறுக்கச்சின் நீளம், b அரைத் துணையச்சின் நீளம்).[5]
- அதிபரவளையத்தின் ஏதாவது ஒரு குவியத்திற்கும் ஒரு அணுகுகோட்டிற்கும் இடையே உள்ள தூரம் b (அரைத் துணையச்சின் நீளம்); குவியத்திலிருந்து அணுகோட்டின் மேல் அமையும் மிக அருகாமையில் அமையும் புள்ளி, அதிபரவளையத்தின் மையத்திலிருந்து a (அரைக் குறுக்கச்சின் நீளம்) அலகு தூரத்தில் இருக்கும்..[1] இவ்விரு கோட்டுத்துண்டுகளையும் தாங்கிப் பக்கங்களாகக் கொண்ட செங்கோணமுக்கோணத்தில் பித்தாகரசு தேற்றப்படி,
- , இங்கு c என்பது அதிபரவளையத்தின் மையத்திற்கும் குவியத்துக்கும் இடைப்பட்டதூரம்.
மேற்கோள்கள்[தொகு]
- ↑ 1.0 1.1 1.2 "காப்பகப்படுத்தப்பட்ட நகல்". Archived from the original on 2016-03-04. பார்க்கப்பட்ட நாள் 2012-07-06.
- ↑ 2.0 2.1 2.2 Spain, Barry. Analytical Conics. Dover Publ., 2007.
- ↑ 3.0 3.1 3.2 [1]
- ↑ 4.0 4.1 "காப்பகப்படுத்தப்பட்ட நகல்". Archived from the original on 2016-03-15. பார்க்கப்பட்ட நாள் 2012-07-06.
- ↑ 5.0 5.1 "காப்பகப்படுத்தப்பட்ட நகல்". Archived from the original on 2012-03-25. பார்க்கப்பட்ட நாள் 2012-07-06.

























