இணைக் கணிப்பீடு
இக்கட்டுரை கூகுள் மொழிபெயர்ப்புக் கருவி மூலம் உருவாக்கப்பட்டது. இதனை உரை திருத்த உதவுங்கள். இக்கருவி மூலம்
கட்டுரை உருவாக்கும் திட்டம் தற்போது நிறுத்தப்பட்டுவிட்டது. இதனைப் பயன்படுத்தி இனி உருவாக்கப்படும் புதுக்கட்டுரைகளும் உள்ளடக்கங்களும் உடனடியாக நீக்கப்படும் |
இணைக் கணிப்பீடு (Parallel computing) என்பது ஒருவகையான கணக்கிடுதல் முறையாகும், இதில் பல கணக்கீடுகள் ஒரே நேரத்தில் செய்யப்படுகிறது,[1] இது பெரும் கணக்குகள் அவ்வப்போது சிறுசிறு கணக்குகளாகப் பிரிக்கப்பட்டு பின்னர் அவை ஒருங்கிசையும் முறையில் ("இணையாக") தீர்க்கப்படும் என்னும் கொள்கையின் கீழ் இயங்குகிறது. பல்வேறு விதமான இணைக் கணிப்பீடு முறைகள் இருக்கின்றன: நுண்மி-நிலை, நெறிமுறைக் கட்டளை நிலை, தரவு மற்றும் செயல் இணைச் செயற்பாடு. இணைச் செயற்பாடு பல ஆண்டுகளாக பயன்படுத்தப்பட்டிருக்கிறது, முக்கியமாக உயர் செயல்பாட்டு கணிப்பீடுகளில், ஆனால் அதிர்வெண் அளவிடுதலைத் தடுக்கும் மெய்யியல் கட்டுப்பாடுகள் காரணமாக சமீப காலங்களில் இதன் மீதான ஆர்வம் பெருகியிருக்கிறது.[2] சமீப காலங்களில் கணினிகளின் மின்ஆற்றல் பயன்பாடு (மேலும் இதன் விளைவாக வெப்ப உற்பத்தி) ஒரு பெரும் விஷயமாக இருப்பதால்,[3] கணினி கட்டமைப்புகளில் இணைக் கணிப்பீடு மோலோங்கிய கருத்தியலாக ஆகியிருக்கிறது, முக்கியமாக பன்மடங்கு உள்ளீட்டு செயலிகள் வடிவில்.[4]
இணைச் செயற்பாட்டினை வன்பொருள் ஆதரிக்கும் நிலைக்கு ஏற்ப இணைக் கணினிகள் தோராயமாக வகுக்கப்படலாம் — பன்மடங்கு-உள்ளீடு மற்றும் பன்மடங்கு செயலி கணினிகள் ஒரு ஒற்றை அமைப்புக்குள்ளாகவே பன்மடங்கு செயல்படுத்தும் கூறுகளைக் கொண்டிருக்கின்றன, அதே நேரத்தில் கிளஸ்டர்கள், எம்பிபிகள் மற்றும் கிரிட்கள்கள் அதே பணியில் வேலை செய்வதற்குப் பல கணினிகளைப் பயன்படுத்துகின்றன. மேம்பட்ட இணைக் கணினி கட்டமைப்புகள் சில நேரங்களில் ஒரு குறிப்பிட்ட பணியைத் துரிதப்படுத்துவதற்குப் பாரம்பரியமிக்க செயலிகளுடன் இணைத்தே பயன்படுத்தப்படுகிறது.
இணைக் கணினி நிரல்களை எழுதுவது வரிசைமுறையிலான ஒன்றை எழுதுவதை விட கூடுதல் கடினமானது,[5] ஏனெனில் உடன்நிகழ்வுகள் பல்வேறு புதிய வகை ஆற்றல் உடைய மென்பொருள் வழுக்களை அறிமுகப்படுத்திக்கொண்டேயிருக்கிறது, அவற்றுள் பந்தய நிலையிலானவை தான் மிகப் பொதுவாக இருப்பது. நல்ல இணை திட்ட செயல்பாட்டைப் பெறுவதற்கு வெவ்வேறு துணைப்பணிக்களுக்கிடையில் இருக்கும் கருத்துப்பரிமாற்றம் மற்றும் ஒரே கால நிகழ்வு தான் எப்போதும் ஒரு பெரும் தடையாக இருக்கிறது.
இணைப்படுத்துதலின் விளைவாக ஒரு நிரலின் வேகப்படுத்தல் அம்தாலின் விதிமுறை என கண்டறியப்பட்டுள்ளது.
பின்னணி[தொகு]
கணினி மென்பொருள் பொதுவாக வரிசைமுறையிலான கணக்கீடுகளுக்காக எழுதப்பட்டது. ஒரு கணக்கிற்கான தீர்வைக் காண்பதற்கு ஒரு படித்தீர்வு கட்டமைக்கப்பட்டு நெறிமுறை கட்டளைகளின் ஒரு தொடர் ஓட்டமாக நடைமுறைப்படுத்தப்படுகிறது. இந்த நெறிமுறைகள் ஒரு கணினியில் மையச் செயற்பகுதியாக செயல்படுத்தப்படுகிறது. ஒரு நேரத்தில் ஒரே ஒரு நெறிமுறை தான் செயல்படுத்தப்படும், அந்த நெறிமுறை முடிவடைந்தவுடன் அடுத்த நெறிமுறை செயல்படுத்தப்படும்.[6]
ஆனால் இணைக் கணிப்பீடுகளோ ஒரு கணக்கினைத் தீர்ப்பதற்கு ஒரே நேரத்தில் பன்மடங்கு செயலிக் கூறுகளைப் பயன்படுத்துகின்றன. ஒவ்வொரு செயலிக் கூறும் தன்னுடைய படித்தீர்வின் பாகத்தை ஒரேநேரத்தில் மற்றவற்றுடன் சேர்ந்து செயல்படுத்தும் விதமாக கணக்கினைச் சார்பற்ற பாகங்களாகப் பிரிப்பதன் மூலம் இது சாத்தியப்படுகிறது. செயலிக் கூறுகள் பல்வேறு வகையினதாகவும், பன்மடங்கு செயலிகளைக் கொண்ட ஒற்றைக் கணினி, பல்வேறு வலைப்பின்னலில் இணைக்கப்பட்ட கணினிகள், மேம்பட்ட வன்பொருள் அல்லது இவை அனைத்தையும் இணைந்த ஒன்று போன்ற மூலங்களைக் கொண்டவைகளாகவும் இருக்கலாம்.[6]
அலைவெண் மதிப்பிடுதல் தான் மத்திய-1980 கள் முதல் 2004 ஆம் ஆண்டு வரை கணினிச் செயல்பாட்டில் மேம்பாடுகளுக்கு முக்கியக் காரணமாக இருந்தது. ஒரு நிரலின் இயங்குநேரம், ஒரு நெறிமுறையின் தோராயமான நேரத்தால் வகுக்கப்படும் நெறிமுறைகளின் எண்ணிக்கைக்கு இணையானது. மற்ற எல்லாவற்றையும் நிலையானதாக வைத்து கடிகார அலைவெண்ணை அதிகரிக்கச் செய்வது, ஒரு நெறிமுறையை செயல்படுத்த எடுத்துக்கொள்ளும் சராசரி நேரத்தைக் குறைத்துவிடும். அலைவெண்ணில் இவ்வாறு அதிகரிக்கச்செய்வது, அனைத்து கணக்கீட்டில் ஒருங்கிணைக்கப்பட்ட நிரல்களின் இயங்குநேரத்தைக் குறைக்கிறது.[7]
எனினும் ஒரு சில்லின் மின்ஆற்றல் பயனீடு P = C × V2 × F என்னும் சமன்பாட்டால் கொடுக்கப்பட்டுள்ளது, இங்கு P என்பது மின்ஆற்றல், C என்பது ஒவ்வொரு கடிகார சுழற்சியால் மின்மாற்றம் செய்யப்படும் மின் தேக்கத்திறன் (உள்ளீடுகள் மாற்றம்கொள்ளும் டிரான்சிஸ்டர்களின் எண்ணிக்கைக்கு விகிதசமமாக), V என்பது மின்னழுத்தம் (voltage) மற்றும் F என்பது செயலி அலைவெண் (நொடியில் ஏற்படும் சுழற்சிகள்).[8] அலைவெண்களில் அதிகரிக்கச் செய்வது ஒரு செயலியில் பயன்படும் மின்ஆற்றலின் அளவை அதிகரிக்கும். செயலி மின்ஆற்றல் பயன்பாட்டை அதிகரிக்கச் செய்தது, இறுதியில் இண்டெல்லின் மே 2004 ஆம் ஆண்டு தன்னுடைய தேஜாஸ் மற்றும் ஜேஹாக் செயலிகளை ரத்து செய்யும் நிலைமையை ஏற்படுத்தியது, மேலோங்கிய கணினி கட்டமைப்பு என்னும் கருத்தியலாக இருந்த அலைவெண் மதிப்பிடுதலின் முடிவு என பொதுவாகக் குறிப்பிடப்படுகிறது.[9]
ஒரு நுண்செயலியில் இருக்கும் டிரான்சிஸ்டரின் அடர்த்தி ஒவ்வொரு 18 முதல் 24 மாதங்களில் இரட்டிப்பாகிறது என்று மோர்ஸ் விதி பட்டறிவான அவதானிப்பாக இருக்கிறது.[10] மின்ஆற்றல் பயனீட்டுச் சிக்கல்கள் மற்றும் அதன் முடிவைப் பற்றிய தொடர்ச்சியான முன் கணிப்புகள் இருந்தபோதிலும் மோர்ஸ் விதி இன்னமும் நடைமுறையில் இருக்கிறது. அலைவெண் மதிப்பிடுதல் முடிவுக்கு வந்ததைத் தொடர்ந்து, இந்தக் கூடுதல் டிரான்சிஸ்டர்கள் (அலைவெண் மதிப்பிடுதலுக்கு இனிமேற்கொண்டு பயன்படுத்தப்படாதவை) இணைக் கணிப்பீடுகளில் கூடுதல் வன்பொருளைச் சேர்ப்பதற்குப் பயன்படுத்தப்படலாம்.
அம்தால்ஸ் விதி மற்றும் குஸ்டாஃப்ச்ன்ஸ் விதி[தொகு]
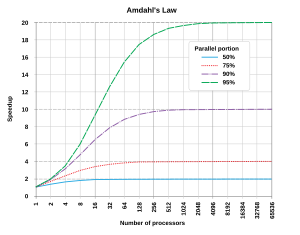
அனுகூலமாக, இணைப்படுத்துதலின் மூலமான வேகமாக்கல் நேரோட்டமுடையதாக இருக்கும் - செயலிக்கூறுகளின் எண்ணிக்கையை இரட்டிப்பாக்குவது இயக்க நேரத்தைப் பாதியாகக் குறைக்கும் மேலும் இரண்டாவது முறையாக இரட்டிப்பாக்குவது இயக்க நேரத்தை மீண்டும் பாதியாகக் குறைக்கும் எனினும் குறைந்த அளவு இணை படித்தீர்வுகளே அனுகூலமான வேகப்படுதலை எட்டும். அவற்றில் பெரும்பாலானவை, சிறு எண்ணிக்கையிலான செயலிக் கூறுகளுக்கு கிட்டத்தட்ட ஒரு நேரோட்ட வேகப்படுதலைக் கொண்டிருக்கின்றன, இது அதிக எண்ணிக்கையிலான செயலிக் கூறுகளுக்கு ஒரு நிலையான மதிப்பீடாக மட்டப்படுத்தப்படுகிறது.
ஒரு இணைக் கணிப்பீடு இயங்குதளத்தில் இருக்கும் படித்தீர்வின் உள்ளார்ந்த வேகப்படுத்துதல் அம்தால்ஸ் விதி முறையால் வழங்கப்படுகிறது, இது முதன்முதலில் ஜீன் அம்தால் அவர்களால் 1960 ஆம் ஆண்டுகளில் முறைப்படுத்தப்பட்டது.[11] அம்தால்சின் விதி கூறுவதாவது, இணைப்படுத்தமுடியாத நிரலின் ஒரு சிறு பகுதி இணைப்படுத்தப்படுதலில் கிடைக்கப்பெறும் ஒட்டுமொத்த வேகப்படுத்தலைக் கட்டுப்படுத்தும். எந்தவொரு பெரிய கணித அல்லது பொறியியல் கணக்கும் வழக்கமாக பல்வேறு இணைப்படுத்தப்பட்ட பாகங்களை மற்றும் பல்வேறு இணைப்படுத்தப்படாத (வரிசைமுறையிலான) பாகங்களையும் கொண்டிருக்கும். இந்தத் தொடர்புமுறை இச்சமன்பாட்டால் வழங்கப்படுகிறது:
இங்கு S என்பது நிரலின் வேகப்படுத்துதலைக் குறிக்கிறது (அதன் அசல் வரிசைமுறையிலான இயக்கநேரத்தின் ஒரு காரணியாக) மற்றும் P என்பது இணைப்படுத்தப்படக்கூடிய பின்னத்தைக் குறிக்கிறது. ஒரு நிரலின் வரிசைமுறையிலான பகுதி இயக்கநேரத்தின் 10% மாக இருந்தால், எத்தனை செயலிகள் சேர்க்கப்படுகிறது என்பது கணக்கில் எடுத்துக்கொள்ளப்படாமல், நமக்கு 10× வேகப்படுத்துதலுக்கு மிகாமல் கிடைக்காது. அதிகமான இணை செயல்படுத்தும் அலகுகளைச் சேர்ப்பதன் பயனுடைமையில் இது உயரெல்லையை இடுகிறது. "வரிசைமுறைப்படுத்தல் கட்டுப்பாடுகளால் ஒரு பணி பகுதிகளாகப் பிரிக்கப்பட முடியாதபோது கூடுதல் முயற்சியைப் பயன்படுத்துவது வேலைத் திட்டத்தில் எந்த விளைவையும் ஏற்படுத்தாது. எத்தனைப் பெண்களை ஈடுபடுத்தினாலும் ஒரு குழந்தையைப் பெற்றெடுக்கும் காலம் ஒன்பது மாதங்களே ஆகும்"[12]
குஸ்டாஃப்சன்ஸ் விமி என்பது கணிப்பீடுகளில் இருக்கும் மற்றொரு விதி இது அம்தாலின் விதிக்கு நெருங்கிய தொடர்புடையது. அது இவ்வாறு முறைப்படுத்தப்படலாம்:
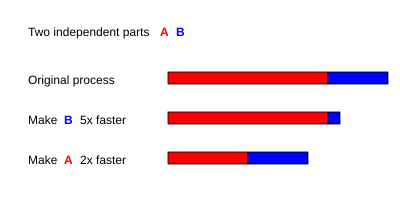
இங்கு P என்பது செயலிகளின் எண்ணிக்கை, S என்பது வேகப்படுத்தலாகும் மற்றும் α என்பது செயல்முறையின் இணைப்படுத்தப்படமுடியாத பாகமாகும்.[13] அம்தாலின் விதி ஒரு நிலையான கணக்கினை மேற்கொள்கிறது மேலும் வரிசைமுறையிலான பிரிவின் அளவு செயலிகளின் எண்ணிக்கைகளின் சார்பற்றவையாக இருக்கின்றன, அதே நேரத்தில் குஸ்டாஃப்சனின் விதி இந்த ஊகங்களை மேற்கொள்வதில்லை.
சார்ந்திருப்பவை[தொகு]
இணை படித்தீர்வுகளை நடைமுறைப்படுத்துவதில் தரவு சார்புடையவைகளைப் புரிந்துகொள்வது அடிப்படையான ஒன்றாகும். சார்ந்திருக்கும் கணக்கீடுகளின் (மாறுநிலைப்பாதை என அறியப்படுவது) நீண்ட தொடர்பினைக் காட்டிலும் வேறெந்த நிரலும் மிக விரைவாக இயங்கிவிடாது, ஏனெனில் தொடர்பில் இருக்கும் முந்துரிமையுடைய கணக்கீடுகளைச் சார்ந்திருக்கும் கணக்கீடுகள் வரிசைமுறையில் செயல்படுத்தப்படவேண்டும். எனினும் பெரும்பாலான படித்தீர்வுகள், சார்ந்திருக்கும் கணக்கீடுகளின் ஒரு நீண்ட தொடரினை மட்டுமே கொண்டிருப்பதில்லை; இணை முறையில் சார்பற்ற கணக்கீடுகளைச் செயல்படுத்துவதற்கான வாய்ப்புகள் வழக்கமாக இருக்கிறது.
Pi மற்றும் Pj இரு நிரல் துண்டுகளாக இருக்கட்டும். பெர்ன்ஸ்டீனின் விதிமுறைகள்[14] இவை இரண்டும் சார்பற்றவையாகவும் இணை முறையில் செயல்படுத்தப்படும்போதும் விவரிக்கின்றன. P i வுக்கு, I i அனைத்து உள்ளீட்டு வேறுபாடாகவும் O i வெளியீட்டு வேறுபாடாகவும் இருக்கட்டும் அதுபோலவே P j க்கும் இருக்கட்டும் . P i மற்றும் P j திருப்திபடுவதாக இருந்தால் அவை சார்பற்றவையாகும்.
முதல் விதிமுறையை மீறுவது ஒரு போக்கினைச் சார்ந்திருக்கும் நிலையை உண்டாக்கும், இது முதல் கூற்றுக்கு ஒத்திசைவானதாக இருக்கக்கூடிய இரண்டாவது கூற்றினால் பயன்படுத்தப்படும் விளைவினை ஏற்படுத்தும். இரண்டாவது விதிமுறை சார்புற்றிருப்பதற்கு எதிரான நிலையைப் பிரதிநிதிக்கிறது, அப்போது இரண்டாவது கூற்று (P j ) முதல் வெளிப்பாடுக்கு (P i ) தேவையான மாறுபாட்டை நீக்கி மேலெழுதும். மூன்றாவது மற்றும் இறுதி விதிமுறை ஒரு வெளியீட்டு சார்புடையதைப் பிரதிநிதிக்கிறது: இரு கூற்றுகள் ஒரே இடத்தில் எழுதப்படும்போது, தர்க்கரீதியாக இறுதி முடிவு கடைசியாக செயல்படுத்தப்பட்ட கூற்றிலிருந்து வரவேண்டும்.[15]
பின்வரும் செயல்பாடுகளைக் கருத்தில்கொள்ளவும், இது பல்வேறு வகையான சார்ந்திருப்பவைகளை எடுத்துக்காட்டுகிறது:
1: function Dep(a, b) 2: c := a·b 3: d := 2·c 4: end function
Dep(a, b) இல் இருக்கும் நடவடிக்கை 3, நடவடிக்கை 2 க்கு முன்னர் செயல்படுத்தப்படமுடியாது, (அல்லது இணை முறையிலும் கூட முடியாது) ஏனெனில் நடவடிக்கை 2 லிருந்து பெறும் ஒரு முடிவினை நடவடிக்கை 3 பயன்படுத்துகிறது. இது விதிமுறை 1 ஐ மீறுகிறது இவ்வாறு அது ஒரு போக்கினைச் சார்ந்திருத்தலை ஏற்படுத்துகிறது
1: function NoDep(a, b) 2: c := a·b 3: d := 2·b 4: e := a+b 5: end function
இந்த எடுத்துக்காட்டில் நெறிமுறைகளுக்கிடையில் எந்த சார்ந்திருத்தலும் இல்லை, அதனால் அவை அனைத்தும் இணை முறையில் இயக்கப்படலாம்.
பெர்ன்ஸ்டீனின் விதிமுறைகள் வெவ்வேறு செயலிகளுக்கிடையில் நினைவகத்தைப் பங்குபோட்டுக்கொள்ள அனுமதிப்பதில்லை. அதற்கு அனுக்கங்களுக்கிடையில் ஒரு ஒழுங்குமுறையை நடைமுறைப்படுத்துவதற்கு அணுகல் குறியீடுகள், அடைப்புகள் அல்லது வேறு ஏதாவது ஒத்தியக்க முறைகள் போன்ற சில வழிமுறைகள் அவசியமாகிறது.
பந்தய நிலைகள், பரிமாற்றுத் தவிர்க்கை, ஒத்தியக்கல் மற்றும் இணை வேகக் குறைவு[தொகு]
ஒரு இணை நிரலில் இருக்கும் உபப்பணிகள் அடிக்கடி திரிகள் (threads) என்று அழைக்கப்படுகிறது. சில இணை கணினிக் கட்டமைப்புகள் இழைகள் எனப்படும் சிறிய, எடைகுறைந்த திரிப் பதிப்புகளைப் பயன்படுத்துகின்றன, அதே நேரத்தில் மற்றவை செயல்முறைகள் எனப்படும் பெரும் பதிப்புகளைப் பயன்படுத்துகின்றன. எனினும் "திரிகள்" என்பது உபப் பணிகளுக்கான ஒரு பொதுவான சொல்லாக ஏற்றுக்கொள்ளப்பட்டுள்ளது. அவற்றுக்கிடையில் பகிர்ந்துகொள்ளப்பட்டும் சில மாறுபாடுகளை திரிகள் அடிக்கடி புதுப்பித்துக் கொள்ள வேண்டியிருக்கிறது. இரு நிரல்களுக்கிடையே இருக்கும் நெறிமுறைகள் எந்தவொரு வரிசைமுறையிலும் இடைவெளியிடப்பட்டிருக்கும். உதாரணத்திற்குப் பின்வரும் நிரலை கருத்தில் கொள்ளுங்கள்:
| திரி A | திரி B |
| 1A: Read variable V | 1B: Read variable V |
| 2A: Add 1 to variable V | 2B: Add 1 to variable V |
| 3A Write back to variable V | 3B: Write back to variable V |
நெறிமுறைகள் 1A மற்றும் 3A வுக்கு இடையில் 1B செயல்படுத்தப்பட்டிருந்தால் அல்லது நெறிமுறைகள் 1B மற்றும் 3B வுக்கு இடையில் நெறிமுறை 1A செயல்படுத்தப்பட்டிருந்தால் நிரலானது தவறான தரவை வெளிப்படுத்தும். இது பந்தய நிலை என அறியப்படுகிறது. பரிமாற்றுத் தவிர்க்கையை வழங்குவதற்கு நிரலாக்குநர் ஒரு பூட்டைப் பயன்படுத்தவேண்டும். இங்கு பூட்டு என்பது ஒரு நிரலாக்க மொழி கட்டமைப்பாகும், இது ஒரு திரியை ஒரு வேறுபாட்டின் மீது கட்டுப்பாடு செலுத்த அனுமதிக்கிறது மற்றும் அந்த வேறுபாட்டின் பூட்டு அவிழ்க்கப்படும் வரையில் இதர திரிகள் அதனைப் படிக்கவும் அதன் மீது எழுதவும் தடை செய்கிறது. பூட்டைக் கொண்டிருக்கும் திரி தன்னுடைய மாறுநிலைப் பிரிவை (சில வேறுபாடுகளுக்கு தனியுரிமை அணுக்கம் தேவைப்படும் நிரலின் பிரிவு) செயல்படுத்துவதில் மற்றும் அது முழுமையடைந்தவுடன் தரவு பூட்டினை அவிழ்ப்பதற்கும் எந்தக் கட்டுப்பாட்டையும் கொண்டிருப்பதில்லை. இதனால் சரியான நிரல் செயல்படுத்துதலை உறுதிப்படுத்துவதற்கு மேலிருக்கும் நிரல் பூட்டைப் பயன்படுத்துவதற்கு பின்வருமாறு மாற்றி எழுதப்படலாம்:
| திரி A | திரி B |
| 1A: Lock variable V | 1B: Lock variable V |
| 2A: Read variable V | 2B: Read variable V |
| 3A: Add 1 to variable V | 3B: Add 1 to variable V |
| 4A Write back to variable V | 4B: Write back to variable V |
| 5A: Unlock variable V | 5B: Unlock variable V |
ஒரு திரி வேறுபாடு V யை வெற்றிகரமாக பூட்டிவிடும், அதே நேரத்தில் இதர திரிகள் பூட்டப்பெற்ற நிலை கொள்ளும்— V மீண்டும் பூட்டு அவிழ்க்கப்படும் வரையில் முன்னரே இயலாததாகிவிடும். இது நிரல் சரிவர செயல்படுதலை உறுதிப்படுத்துகிறது. பூட்டுகள் சரியான நிரல் செயல்படுதலை உறுதிப்படுத்துவதற்குத் தேவைப்பட்ட போதிலும் ஒரு நிரலை பெருமளவில் மெதுவாக செயல்பட வைக்கும்.
அணுவற்ற பூட்டுகளைப் பயன்படுத்தி பன்மடங்கு வேறுபாடுடையவற்றைப் பூட்டுவது நிரல் முடக்கம் அடையும் வாய்ப்பினைக் கொண்டிருக்கிறது. ஒரு அணு பூட்டு பன்மடங்கு வேறுபாடுடையவை அனைத்தையும் ஒரே நேரத்தில் பூட்டிவிடுகிறது. அதனால் எல்லாவற்றையும் பூட்ட முடியாவிட்டால், எந்த ஒன்றையும் அது பூட்டாது. இரு திரிகள் ஒவ்வொன்றும் அணுவற்ற பூட்டுகளைப் பயன்படுத்தி ஒரே இரு வேறுபாடுடையவற்றைப் பூட்ட வேண்டியிருந்தால், அவற்றில் ஒன்றை ஒரு திரியும் இரண்டாவது திரி இரண்டாவது வேறுபாடுடையவற்றைப் பூட்டும் சாத்தியக்கூறுகள் இருக்கின்றன. அத்தகைய ஒரு நிலையில் இரு திரிகளும் முழுமைப்படுத்தாது மற்றும் முடிவுகளை முடக்கும்.
பல இணை நிரல்களுக்கு தங்கள் உபப் பணிகள் ஒத்தியக்கத்தில் செயல்பட வேண்டியிருக்கிறது. இதற்கு அடைப்புகளின் பயன்பாடு தேவைப்படுகிறது. அடைப்புகள் வழக்கமாக ஒரு மென்பொருள் பூட்டைப் பயன்படுத்தி செயற்படுத்தப்படுகிறது. பூட்டுகளற்ற மற்றும் காத்திருப்புகளற்ற படித்தீர்வுகள் எனப்படும் படித்தீர்வுகளின் ஒரு பிரிவு ஒட்டுமொத்தமாக பூட்டுகள் மற்றும் அடைப்புகளின் பயன்பாட்டைத் தவிர்க்கிறது. எனினும், இந்த அணுகுமுறையை நடைமுறைப்படுத்துவது பொதுவாகவே கடினமானதாகும் மேலும் அதற்கு சரியாக வடிவமைக்கப்பட்ட தரவுக் கட்டமைப்புகள் தேவைப்படுகிறது.
எல்லா இணைப்படுத்தப்படுதல்களும் வேகமாக்கப்படும் விளைவை அடைவதில்லை. பொதுவாக, ஒரு பணி மேலும் மேலும் திரிகளாக உடைக்கப்படும் போது அந்தத் திரிகள் தங்களுடைய எப்போதுமே அதிகரித்துவரும் நேரப் பகுதியை ஒன்றுடன் மற்றொன்று தகவல்தொடர்பு கொள்வதிலேயே செலவிடுகின்றன. இதன் விளைவாக, சிக்கலைத் தீர்ப்பதில் எடுத்துக்கொள்ளப்படும் நேரத்தின் பெரும்பகுதி தகவல்தொடர்பு ஆக்கிரமித்துக்கொள்கிறது மற்றும் கூடுதலான இணைப்படுத்தப்படுதல் (அதாவது, வேலைப்பளுவை மேலும் அதிக திரிகளுக்குப் பிரித்துக்கொடுத்தல்) முழுமைப்படுத்தலுக்குத் தேவைப்படும் நேர அளவினைக் குறைப்பதற்குப் பதிலாக அதிகரிக்கச் செய்கிறது. இது இணை வேகக் குறைப்பு என அறியப்படுகிறது.
நுண்ணிய இழையமைப்பு, செப்பமற்ற இழையமைப்பு மற்றும் இக்கட்டான இணைச் செயற்பாடு[தொகு]
பயன்பாட்டுச் செயலிகளின் உபப் பணிகள் எவ்வளவு அடிக்கடி ஒத்தியலவேண்டும் அல்லது ஒன்றுடன் மற்றொன்று தொடர்பு கொள்கிறது என்பதைப் பொறுத்து அவை அடிக்கடி வகைப்படுத்தப்படுகின்றன. பயன்பாட்டுச் செயலிகளின் உபப் பணிகள் ஒரு நொடிக்குப் பல முறை தொடர்பு கொள்ள வேண்டியிருந்தால் அது நுண்ணிய இழையமைப்பு இணைச் செயற்பாட்டை வெளிப்படுத்துகிறது; அது நொடிக்குப் பலமுறை தொடர்பு கொள்ளாதிருந்தால் அது செப்பமற்ற இழையமைப்பு இணைச் செயற்பாட்டை வெளிப்படுத்துகிறது மேலும் அவை எப்போதாவது அல்லது தொடர்பே கொள்ளாமல் இருந்தால் இக்கட்டுக்குரிய இணை ஆக இருக்கிறது. இக்கட்டான இணை பயன்பாடுச் செயலிகள் தான் இணைப்படுத்துவது மிகச் சுலமான ஒன்றாகக் கருதப்படுகிறது.
நிலையாயிருக்கும் மாதிரிகள்[தொகு]
இணை நிராலாக்கி மொழிகள் மற்றும் இணை கணினிகள் நிலையாயிருக்கும் மாதிரியைக் (நினைவக மாதிரி என்றும் அறியப்படும்) கொண்டிருக்கவேண்டும். கணினி நினைவகத்தில் இயக்கங்கள் எவ்வாறு நிகழ்கின்றன மற்றும் விளைவுகள் எவ்வாறு ஏற்படுகின்றன என்பதற்கான விதிமுறைகளை நிலையாயிருக்கும் மாதிரி வரையறுக்கிறது.
நிலையாயிருக்கும் மாதிரிகளில் முதலில் தோன்றியவற்றில் லெஸ்லீ லாம்போர்ட்டின் வரிசைமுறையிலான நிலையாயிருக்கும் மாதிரி ஒன்றாகும். வரிசைமுறையிலான நிலையாயிருக்கும் ஒரு இணை நிரலின் பண்பாகும், அதன் இணை செயற்பாங்கு ஒரு வரிசைமுறையிலான் நிரல் ஏற்படுத்தும் அதே முடிவுகளை இதுவும் ஏற்படுத்தும். குறிப்பாக, "ஏதோவொரு வரிசைமுறையில் எல்லாச் செயலிகளின் இயக்கங்களும் செயல்படுத்தப்பட்டிருப்பதுபோல் எந்தவொரு செயல்பாட்டின் முடிவுகளும் ஒன்றுபோலவே இருந்தால் மற்றும் ஒவ்வொரு தனிப்பட்ட செயலியின் இயக்கங்களும் அதன் செயலி வரைமுறைப்படுத்திய முறையில் இந்த வரிசைமுறையில் தோன்றினால்" ஒரு நிரல் வரிசைமுறையிலான நிலையாயிருக்கும்.[16]
மென்பொருள் பரிமாற்றத்துக்குரிய நினைவகம் பொதுவாக இருக்கும் நிலையாயிருக்கும் மாதிரி. மென்பொருள் பரிமாற்றத்துக்குரிய நினைவகம், அணு பரிமாற்றங்கள் என்னும் கருத்துப்படிவத்தை தரவுத்தள கோட்பாடுகளிலிருந்து பெற்று அவற்றை நினைவக அணுக்கத்திற்குப் பொருத்துகிறது.
கணிதரீதியாக இந்த உருமாதிரிகள் பல்வேறு வழிமுறைகளில் பிரதிநிதிக்கப்படலாம். கார்ல் ஆதாம் பெட்ரியின் 1962 ஆம் ஆண்டு முனைவர் பட்ட ஆய்வேட்டில் அறிமுகப்படுத்தப்பட்ட பெட்ரி நெட், நிலையாயிருக்கும் மாதிரிகளின் விதிமுறைகளைத் தொகுத்தளிக்கும் ஆரம்ப கால முயற்சியாக இருந்தது. பின்னர் இவற்றின் மீது தரவோட்டக் கோட்பாடு உருவாக்கப்பட்டது மற்றும் தரவோட்டக் கோட்பாடுகளின் எண்ணங்களை மெய்யியலாக நடைமுறைப்படுத்த தரவோட்ட கட்டமைப்புகள் உருவாக்கப்பட்டது. 1970 ஆம் ஆண்டுகளின் இறுதிகள் முதலே இடைவினைபுரியும் கூறுகளால் உருவாக்கப்பட்ட அமைப்புகளைப் பற்றிய இயற்கணிப்புக்குரிய காரண ஆய்வை அனுமதிக்கும் விதமாக தொடர்புகொள்ளும் அமைப்புகளின் நுண்கணிதம் மற்றும் தொடர்புகொள்ளும் வரிசைமுறையிலான செயற்பாடு போன்ற செயற்பாட்டு கணிப்பு உருவாக்கப்பட்டன. π-நுண்கணிதம் போன்ற செயற்பாட்டு நுண்கணித குடும்பத்தில் மிகச் சமீபத்திய சேர்த்தல்கள் ஆற்றல்மிகு பரப்புருக்களைப் பற்றிய காரண அறிவைப் பெறுவதற்கான ஆற்றல்களைச் சேர்த்துள்ளன. லாம்போர்ட்டின் TLA+ போன்ற தருக்கமுறைகள் மற்றும் கணிதத்திறகுரிய மாதிரிகளான வரைதல் மற்றும் ஆக்டர் ஈவண்ட் வரைபடங்கள் கூட ஒருங்கிசையும் அமைப்புகளின் நடத்தையைப் பற்றி விவரிப்பதற்காக உருவாக்கப்பட்டிருக்கிறது.
ஃப்ளைன்னின் பாகுபாட்டியல்[தொகு]
மைக்கல் ஜெ. ஃப்ளைன் இணை (மற்றும் வரிசைமுறையிலான) கணினிகள் மற்றும் நிரல்களுக்கான ஆரம்பகால வகைப்பாட்டு அமைப்புகளை உருவாக்கினார், இப்போது அது ஃப்ளைன்னின் பாகுபாட்டியல் என்று அறியப்படுகிறது. ஃப்ளைன் நிரல்கள் மற்றும் கணினிகளை அவை ஒரு ஒற்றைத் தொகுப்பு நெறிமுறைகள் அல்லது பன்மடங்கு தொகுப்பு நெறிமுறைகளைப் பயன்படுத்தி இயங்குகின்றனவா, இந்த நெறிமுறைகள் ஒற்றை அல்லது பன்மடங்கு தரவுத் தொகுப்புகளைப் பயன்படுத்துகின்றனவா இல்லையா என்பதைக் கொண்டு வகைப்படுத்தினார்.
ஒற்றை-நெறிமுறை-ஒற்றை-தரவு (SISD) வகைப்பாடு ஒட்டுமொத்த வரிசைமுறையிலான நிரலுக்குச் சமமானது. ஒற்றை-நெறிமுறை-பன்மடங்கு-தரவு (SIMD) வகைப்பாடு, ஒரு பெரும் தரவு தொகுப்பில் அதே இயக்கத்தை மீண்டும் மீண்டும் செய்வதற்கான ஒரு செயலொத்ததாகும். இது பொதுவாக சமிக்கை செயல்பாட்டுப் பயன்பாடுகளில் செய்யப்படுகிறது. பன்மடங்கு-நெறிமுறை-ஒற்றை-தரவு (MISD) அரிதாக பயன்படுத்தப்படும் வகைப்பாடாகும். இதை எதிர்கொள்வதற்கான கணினி கட்டமைப்புகள் உருவாக்கப்பட்டபோதிலும் (சுருக்க அணி போன்றவை), இந்த வகைக்குப் பொருந்தக்கூடிய சில பயன்பாடுகளே உருவெடுத்தன. பன்மடங்கு-நெறிமுறை-பன்மடங்கு-தரவு (MIMD) நிரல்கள் தான் மிகப் பொதுவாகக் காணப்படும் இணை நிரல் வகைகளாகும்.
டேவிட் ஏ. பாட்டர்சன் மற்றும் ஜான் எல். ஹென்னெச்சி ஆகியோரின் கூற்றுப்படி, "சில கணினிகள் இந்த வகைகளின் கலப்பினம்தான், ஆனால் இந்த செம்மையான மாதிரிகள் எளிமையாகவும், புரிந்துகொள்வது எளிதாகவும் மற்றும் நல்ல முதல் அணுகுதலை வழங்குவதாலும் இது நிலைகொண்டிருக்கிறது. மிகவும் பரவலாகப் பயன்படுத்தப்படும் திட்டமுமாக இது இருக்கிறது-ஒருவேளை அதன் புரிந்துகொள்ளும் தன்மையால் இருக்கலாம்."[17]
இணைச் செயற்பாடு வகைகள்[தொகு]
நுண்மி-நிலை இணைச் செயற்பாடு[தொகு]
மிகப் பெரிய அளவிலான தொகையீடு (VLSI) கணினிச்-சில்லு கட்டுமானத் தொழில்நுட்பம் 1970 ஆம் ஆண்டுகளில் வருகைபுரிந்ததுமுதல் சுமார் 1986 ஆம் ஆண்டு வரையில், கணினி கட்டமைப்பில் வேகப்படுத்துதல் கணிப்பொறிச் சொல் அளவு, அதாவது ஒரு சுழற்சிக்குச் செயலி கையாளக்கூடிய தகவல்களின் அளவு, இரட்டிப்பாக்கத்தால் இயக்கப்படுகிறது.[18] சொல் அளவை அதிகரிக்கச்செய்வது, ஒரு சொல்லின் நீளத்தைவிட பெரியதாக இருக்கும் மாறுபாடுகளின் மீதான இயக்கங்களை மேற்கொள்ள செயலி செயல்படுத்தவேண்டிய நெறிமுறைகளின் எண்ணிக்கையைக் குறைக்கிறது. உதாரணத்திற்கு ஒரு 8-நுண்ம செயலி இரண்டு 16-நுண்ம முழு எண்களைச் சேர்க்கவேண்டும், செயலி முதலில் வழக்கமான கூட்டல் நெறிமுறையைப் பயன்படுத்தி ஒவ்வொரு முழு எண்ணிலிருந்தும் 8 கீழ்-நிலை நுண்மிகளைச் சேர்க்கவேண்டும் அதன் பின்னர் முன்னெடுத்துச் செல் உடன் கூட்டல் நெறிமுறையைப் பயன்படுத்தி 8 உயர்-நிலை நுண்மிகளையும் கீழ் நிலை கூட்டலிலிருந்து முன்னெடுத்துச் செல் நுண்மியையும் சேர்க்கவேண்டும்; இவ்வாறு ஒரு 8-நுண்ம செயலிக்கு ஒரு ஒற்றை இயக்கத்தை நிறைவுசெய்வதற்கு இரு நெறிமுறைகள் தேவைப்படுகின்றது, அதே நேரத்தில் 16-நுண்ம செயலி அதே இயக்கத்தை ஒரு ஒற்றை நெறிமுறையில் நிறைவுசெய்ய முடியும்.
வரலாற்று ரீதியாக 4-நுண்ம நுண்செயலிகள் 8-நுண்ம பின்னர் 16-நுண்ம மற்றும் அதன் பின்னர் 32-நுண்ம நுண்செயலிகளால் மாற்றியிடப்பட்டது. 32-நுண்ம செயலிகளின் அறிமுகத்துடன் இந்தப் போக்கு பொதுவாக ஒரு முடிவுக்கு வந்தது, இரு பத்தாண்டுகளாக இது தான் பொதுப்பயன் கணிப்பீடுகளில் வழக்கமாய் இருந்துவருகிறது. சமீப காலங்களில் (2003–2004 ஆம் ஆண்டுகள்), x86-64 கட்டுமானங்களின் வருகைக்குப்பின்னர், 64-நுண்ம செயலிகள் பொதுவானவையாகிவிட்டன.
நெறிமுறை-நிலை இணைச் செயற்பாடு[தொகு]

ஒரு கணினி நிரல் என்பது, சுருக்கமாக, ஒரு செயலியால் செயல்படுத்தப்படும் நெறிமுறைகளின் தொகுப்பாகும். இந்த நெறிமுறைகள் மாற்றியமைக்கப்படலாம் மற்றும் குழுக்களாக இணைக்கப்படலாம் அவை பின்னர் நிரலின் முடிவினை மாற்றாமல் இணையில் செயல்படுத்தப்படுகிறது. இது நெறிமுறை-நிலை இணைச் செயற்பாடு என அறியப்படுகிறது. நெறிமுறை நிலை இணைச் செயற்பாடுகளின் முன்னேற்றங்கள் மத்திய 1980 முதல் மத்திய 1990 ஆம் ஆண்டுகள் வரையில் கணினி கட்டமைப்புகளில் ஆதிக்கம் செலுத்தி வந்தது.[19]
நவீன செயலிகள் பன்மடங்கு நிலை நெறிமுறை குழாய்த்தொடர்களைக் கொண்டிருக்கின்றன. குழாய்த்தொடரின் ஒவ்வொரு கட்டமும் அந்தக் கட்டத்தில் அந்த நெறிமுறைகளின் மீது செயலி மேற்கொள்ளும் வெவ்வேறு செயல்களுக்குப் பொருந்தியிருக்கிறது; N-கட்ட குழாய்த்தொடரினைக் கொண்டிருக்கும் ஒரு செயலி முழுமைப்படுத்தும் பல்வேறு காலகட்டங்களில் வெவ்வேறு N வரையிலான நெறிமுறைகளைக் கொண்டிருக்கலாம். ஒரு குழாய்தொடர் செயலியின் ஒழங்குமுறையான உதாரணமாக இருப்பது RISC செயலி, இது ஐந்து கட்டங்களைக் கொண்டிருக்கிறது: நெறிமுறை கொணர்தல், குறியீடு நீக்கம், செயல்படுத்தல், நினைவக அணுக்கம் மற்றும் திரும்ப எழுது. பெண்டியம் 4 செயலி 35-கட்ட குழாய்த் தொடரினைக் கொண்டிருந்தது.[20]
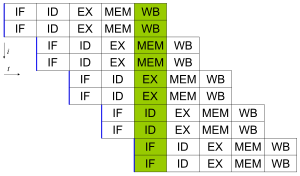
குழாய்த்தொடரமைப்பிலிருந்து பெறப்படும் நெறிமுறை-நிலை இணைச் செயற்பாடு அல்லாமல் சில செயலிகள் ஒரே நேரத்தில் ஒன்றுக்கும் மேற்பட்ட நெறிமுறைகளை வழங்கும். இவை சூப்பர்ஸ்கேலார் செயலிகள் என்று அழைக்கப்படுகின்றன. அவற்றுக்கிடையில் தரவு சார்ந்திருத்தல் இல்லாமலிருந்தால் மட்டுமே நெறிமுறைகள் ஒன்றாக இணைக்கப்படலாம். ஸ்கோர்போர்டிங் மற்றும் டோமாசுலோ படித்தீர்வு (இது ஸ்கோர்போர்டிங்கிற்கு ஒத்திருக்கிறது ஆனால் பதிவை மறுபெயரிடுதலைப் பயன்படுத்துகிறது) ஆகிய இரண்டும் தான் வரிசை முறைக்கு வெளியிலான செயல்படுத்துதல் மற்றும் நெறிமுறை நிலை இணைச் செயற்பாடுகளை நடைமுறைப்படுத்துவதற்கு மிகப் பொதுவான தொழில்நுட்பங்களாகும்.
தரவு இணைச் செயற்பாடு[தொகு]
தரவு இணைச் செயற்பாடு என்பது நிரல் முழுச்சுற்றுகளில் பொதிந்துள்ள இணைச் செயற்பாடாகும், இது இணைகளில் செயல்முறைப்படுத்தப்படவேண்டிய பல்வேறு கணிப்பீடு கணுக்களிடையே தரவைப் பகிர்ந்தளிப்பதில் கவனம் செலுத்தும். "முழுச்சுற்றுகளை இணைப்படுத்துவது அடிக்கடி ஒத்த (ஒன்றுபோலவே இருக்கும் என்பதில்லை) இயக்க வரிசை முறைகளுக்கு அல்லது பெரும் தரவுக் கட்டமைப்பின் கூறுகளின் மீது மேற்கொள்ளப்பட்டும் செயல்களுக்கு இட்டுச்செல்லும்"[21] பல அறிவியல் மற்றும் பொறியியல் பயன்பாடுகள் தரவு இணைச் செயற்பாட்டை வெளிப்படுத்துகிறது.
முழுச்சுற்று கொண்டு செல்லலைச் சார்ந்திருப்பவை ஒன்று அல்லது கூடுதல் முந்தைய மறுசெய்கையின் வெளியீடுகளின் முழுச்சுற்று மறுசெய்கையைச் சார்ந்தவையாக இருக்கின்றன. முழுச்சுற்று கொண்டு செல்லலைச் சார்ந்திருப்பவை முழுச்சுற்றுகள் இணைப்படுத்தப்படுவதைத் தடுக்கின்றன. உதாரணத்திற்கு, முதல் சில ஃபைபோனாக்கி எண்களை கணிப்பீடு செய்யக்கூடிய பின்வரும் போலிக்குறியீட்டை கவனிக்கவும்:
1: PREV1 := 0 2: PREV2 := 1 4: do: 5: CUR := PREV1 + PREV2 6: PREV1 := PREV2 7: PREV2 := CUR 8: while (CUR < 10)
இந்த முழுச்சுற்று இணைப்படுத்தப்படமுடியாது, ஏனெனில் CUR தன்னையும் (PREV2) மற்றும் PREV1 ஐயும் சார்ந்திருக்கிறது, இவை ஒவ்வொரு முழுச்சுற்று மறுசெய்கையில் கணிப்பீடு செய்யப்படுகிறது. ஒவ்வொரு மறுசெய்கையும் முந்தைய ஒன்றின் முடிவினைச் சார்ந்திருப்பதால் அவை இணையில் செயல்புரிய முடியாது. ஒரு கணக்கின் அளவு பெரிதாக ஆகவும், கிடைக்கப்பெறும் தரவு-இணைச் செயற்பாட்டின் அளவும் கூட பெரிதாக ஆகிறது.[22]
செயல் இணைச் செயற்பாடு[தொகு]
செயல் இணைச் செயற்பாடு என்பது "ஒரே தரவுத் தொகுப்பு அல்லது வெவ்வேறு தரவுத் தொகுப்பு ஆகிய எதிலும் ஒட்டுமொத்தமாக வெவ்வேறு கணக்கீடுகளை நிகழ்த்தக்கூடிய" ஒரு இணை நிரலின் பண்புக்கூறாகும்.[21] இது தரவு இணைச் செயற்பாட்டுடன் வேறுபடுகிறது, இங்கு அதே தரவு அல்லது வெவ்வேறு தரவு தொகுப்புகளில் ஒரே கணக்கீடு நிகழ்த்தப்படுகிறது. செயல் இணைச் செயற்பாடு வழக்கமாக கணக்கின் அளவின் விகிதத்துடன் இருப்பதில்லை.[22]
வன்பொருள்[தொகு]
நினைவகம் மற்றும் தகவல்தொடர்பு[தொகு]
ஒரு இணைக் கணினியில் இருக்கும் பிரதான நினைவகம், ஒன்று பகிர் நினைவகமாக (ஒரு ஒற்றை முகவரி இடம் அனைத்து செயல்பாட்டுக் கூறுகளால் பகிர்ந்துகொள்ளப்படுகிறது) இருக்கும் அல்லது பரப்பிய நினைவகமாக இருக்கும் (இதில் ஒவ்வொரு செயல்பாட்டுக் கூறும் தனதே ஆன ஒரு இடஞ்சார்ந்த முகவரி இடத்தைக் கொண்டிருக்கும்).[23] நினைவகம் தர்க்கரீதியாக பரவியிருக்கும் தன்மையையே பரவிய நினைவகம் குறிப்பிடுகிறது, ஆனால் அடிக்கடி அது மெய்யியலாக பரவியிருப்பதையும் கூட வலியுறுத்துகிறது. பரவிய பகிர்வு நினைவகம் மற்றும் நினைவகம் மெய்நிகராக்கல் ஆகியவை இந்த இரு அணுகுமுறைகளையும் இணைக்கின்றன, இதில் செயல்பாட்டுக் கூறுகள் தனதே ஆன ஒரு இடஞ்சார்ந்த நினைவகமும் இடஞ்சாரா செயலிகளில் இருக்கும் நினைவகத்திற்கான அணுக்கத்தையும் கொண்டிருக்கிறது. இடஞ்சார்ந்த நினைவகத்திற்கான அணுக்கம் இடஞ்சாராத நினைவகத்திற்கான அணுக்கத்தை விட வழக்கமாக வேகமாக இருக்கும்.
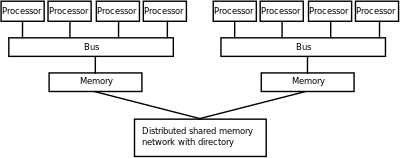
பிரதான நினைவகத்தின் ஒவ்வொரு கூறும் சமமான மறைநிலை மற்றும் பட்டயகலத்துடன் அணுக்கம் செய்யக்கூடிய கணிப்பொறி கட்டமைப்புகள் சமச்சீரான நினைவக அணுக்க (Uniform Memory Access) (UMA) அமைப்புகள் என்று அறியப்படுகிறது. வழக்கமாக இது ஒரு பகிர்ந்த நினைவக அமைப்பால் மட்டுமே சாத்தியப்படும், இதில் நினைவகம் மெய்யியலாக பரவியில்லை. இந்தப் பண்புக்கூறுகளைக் கொண்டிராத ஒரு அமைப்பு சமச்சீரற்ற நினைவக அணுக்க (NUMA) கட்டமைப்பு என்று அறியப்படுகிறது. பரவிய நினைவக அமைப்புகள் சமச்சீரற்ற நினைவக அணுக்கத்தைக் கொண்டிருக்கின்றன.
கணிப்பொறி அமைப்புகள் சேமிப்பகங்களைப் பயன்படுத்திக்கொள்கின்றன— சிறிய, வேகமான நினைவகங்களான இவை செயலிக்கு மிக அருகில் அமைந்திருப்பதுடன் நினைவக மதிப்புகளின் தற்காலிக பிரதிகளைச் சேமிக்கின்றன (மெய்யியல் மற்றும் தர்க்கரீதியான பொருளில் இரண்டிற்கும் அருகில்). ஒரே மதிப்பீட்டை ஒன்றுக்கும் மேற்பட்ட இடத்தில் சேமிக்கும் சேமிப்பிடங்களுடன் இணைக் கணிப்பொறி அமைப்புகள் சில பிரச்சனைகளைக் கொண்டிருக்கின்றன, இதில் தவறான நிரல் செயல்படும் சாத்தியக்கூறுகள் இருக்கின்றன. இந்தக் கணினிகளுக்கு ஒரு சேமிப்பக ஓத்திணக்க அமைப்புகள் தேவைப்படுகின்றன, இவை சேமிக்கப்பட்ட மதிப்பீடுகளின் தடத்தைக் கண்காணித்து அவற்றைப் பயன்படத்தகும் வகையில் துப்புரவாக்கிச் சரியான நிரல் செயல்படுதலை உறுதிப்படுத்துகிறது. எந்த மதிப்பீடுகள் அணுக்கம் செய்யப்படுகின்றன (மற்றும் இதன் மூலம் துப்பரவாக்கப்படவேண்டும்) என்பதைக் கண்காணிப்பதற்கான மிகப் பொதுவான வழிமுறைகளில் ஒன்றாக இருப்பது மின்வாய் தலையீடு. கணிப்பொறி கட்டமைப்பில் மிகப்பெரிய, உயர் செயல்பாட்டு சேமிப்பக ஒத்திணக்க அமைப்புகளை வடிவமைப்பது மிக்க் கடுமையான சிக்கலாகும். இதன் விளைவாக, பகிர்ந்த நினைவக கணிப்பொறி கட்டமைப்புகள் பரவியிருக்கும் நினைவக அமைப்புகள் செய்வதைப் போல் ஏற்றம்கொள்வதில்லை.[23]
செயலி-செயலி மற்றும் செயலி-நினைவக தகவல்தொடர்பு ஒரு வன்பொருளில் பல்வேறு வழிமுறைகளில் நடைமுறைப்படுத்தப்படலாம், அவற்றில் பகிர்ந்த (பல்துறை அல்லது பல்கூட்டச் செலுத்தி எதுவாகவும் இருக்கலாம்) நினைவகம், ஒரு குறுக்குத்தண்டு இணைப்புமாற்றி, பகிர்ந்த மின்வாய் அல்லது நட்சத்திர, மோதிர, மர, மிகை கனசதுரம், தடித்த மிகை கனசதுரம் (ஒரு கணுவிடத்தில் ஒன்றுக்கும் மேற்பட்ட செயலியைக் கொண்ட ஒரு மிகை கனசதுரம்) உட்பட கணக்கிலடங்கா பரப்புருகளின் ஒரு சேர்த்திணைத்த பிணையம் அல்லது n-பரிமாண வலை ஆகிய வழிமுறைகளும் இதில் அடங்கும்.
சேர்த்திணைத்த பிணையத்தை ஆதாரமாகக் கொண்ட இணை கணினிகளுக்கு, நேரடியாக இணைக்கப்படாத கணுக்களிடையே தகவல்களை அனுப்ப இயலச் செய்வதற்கு ஏதோவொரு வகை வழியிடல் தேவைப்படுகிறது. செயலிகளுக்கிடையில் தகவல்தொடர்புக்குப் பயன்படுத்தப்படும் ஊடகம், பெரும் பல்செயலிகளில் படிநிலை முறையாக இருக்கவே வாய்ப்பிருக்கிறது.
இணைக் கணினிகளின் பிரிவுகள்[தொகு]
இணைச் செயற்பாட்டை வன்பொருள் ஆதரிக்கும் நிலைக்கு ஏற்ப தோராயமாக இணை கணினிகள் வகைப்படுத்தப்படலாம். இந்த வகைப்படுத்தல் அடிப்படை கணிப்பீட்டு கணுக்களுக்கிடையிலான தூரத்திற்கு ஏற்ப பரந்துவிரிந்து தொடர்புடையதாக இருக்கிறது. இவை ஒன்றையொன்று விலக்கும் தன்மையுடையவையல்ல; உதாரணத்திற்கு சமச்சீர்மையுடைய பல்செயலிகள் ஒப்பீட்டளவில் பொதுவானதாக இருக்கிறது.
பல்அகடு (multicore) கணிப்பீடு[தொகு]
ஒரு பல்அகடு செயலி என்பது ஒரே சில்லில் பன்மடங்கு செயல்படுத்தும் அலகுகளை ("அகடுகள்") உள்ளடக்கியிருக்கும் ஒரு செயலியாகும். இந்தச் செயலிகள் சூப்பர்ஸ்கேலார் செயலிகளிடமிருந்து வேறுபடுகின்றன, இவை ஒரு நெறிமுறை தொகுப்பிலிருந்து (திரி) ஒரு சுழற்சிக்குப் பன்மடங்கு நெறிமுறைகளை வழங்கமுடியும்; இதற்கு நேர்மாறாக ஒரு பல்அகடு செயலி பன்மடங்கு நெறிமுறை தொகுப்பிலிருந்து பன்மடங்கு நெறிமுறைகளை வழங்கும். ஒரு பல்அகடு செயலியிலிருக்கும் ஒவ்வொரு அகடும் ஒரு சூப்பர்ஸ்கேலாராகவும் இருக்கும் வாய்ப்பு கொண்டிருக்கிறது, அதாவது ஒவ்வொரு சுழற்சியிலும் ஒவ்வொரு அகடும் ஒரு நெறிமுறை தொகுப்பிலிருந்து பன்மடங்கு நெறிமுறைகளை வழங்கமுடியும்.
உடன்நிகழ்கிற பல்புரியாக்கம் (இதில் இன்டெல்லின் உயர்புரியாக்கம் மிகப் பிரபலமானது) போலி-பல்அகடின் ஆரம்பகால வடிவமாக இருந்தது. உடன்நிகழ்கிற பல்புரியாக்க திறன்கொண்ட ஒரு செயலி ஒரேயொரு செயல்படுத்தும் அலகைக் ("அகடு") கொண்டிருக்கிறது, ஆனால் செயல்படுத்தப்படும் அலகு வெறுமனே இருக்கும்போது (சேமிப்பக தவறல் போன்றவைகளின் போது), அது அந்த செயல்படுத்தும் அலகை இரண்டாவது திரியைச் செயல்படுத்துவதற்குப் பயன்படுத்துகிறது. சோனி பிளேஸ்டேஷன் 3 இல் பயன்படுத்துவதற்காக வடிவமைக்கப்பட்ட ஐபிஎம்-மின் மின்கல நுண்செயலி, முக்கிய பல்அகடு செயலிகளில் ஒன்றாகும்.
சமச்சீரான பல்செயலாக்கம்[தொகு]
ஒரு சமச்சீரான பல்செயலாக்கம் (SMP) என்பது, நினைவகத்தைப் பகிர்ந்துகொண்டு ஒரு மின்வாய் மூலம் இணைப்பு கொள்ளும் பன்மடங்கு ஒத்த செயலிகளுடன் கூடிய ஒரு கணிப்பொறி அமைப்பாகும்.[24] மின்வாய் பூசல்கள் மின்வாய் கட்டமைப்புகள் வரையறைப்படுத்துவதைத் தடுக்கின்றன. இதன் விளைவாக சமச்சீரான பல்செயலாக்கங்கள் பொதுவாக 32 செயலிகளுக்கு மேல் கொண்டிருப்பதில்லை.[25] "செயலிகளின் சிறிய அளவு மற்றும் பெரும் சேமிப்பகங்களால் சாதிக்கப்பட்ட மின்வாய் பட்டையகலங்களுக்கான தேவையில் கணிசமான குறைப்பு ஆகிய காரணங்களால் அத்தகைய சமச்சீரான பல்செயலாக்கங்கள் பெரிதும் விலை குறைந்திருக்கிறது, ஆனால் போதிய அளவுக்கான நினைவக பட்டையகலம் இருக்கும் பட்சத்தில் இது சாத்தியம்."[24]
விரவல் கணிப்பீடு[தொகு]
விரவல் கணினி (பரவியிருக்கும் நினைவக பல்செயலி என்றும் அறியப்படுவது) என்பது ஒரு பரவியிருக்கும் நினைவக கணிப்பொறி அமைப்பாகும், இதில் செயல்பாட்டு கூறுகள் ஒரு வலையமைப்பு மூலம் இணக்கப்பட்டிருக்கிறது. விரவல் கணினிகள் அதிக அளவில் மாற்றம்கொள்ளத்தக்கது.
கொத்துக் (கிளஸ்டர்) கணிப்பீடு[தொகு]

ஒரு கிளஸ்டர் என்பது தளர்வாக பிணைக்கப்பட்ட நெருங்கி ஒன்றாகப் பணிபுரியும் கணினிகளின் ஒரு குழுவாகும், அப்போதுதான் அவை ஏதோவொரு வகையில் ஒரு ஒற்றைக் கணினியாகக் கருதப்படும்.[26] ஒரு வலைப்பின்னல் மூலம் இணைக்கப்பட்ட பன்மடங்கு தனித்தியங்கு அமைப்புகளால் கிளஸ்டர்கள் இயற்றப்படுகின்றன. கொத்தில் இருக்கும் கணிப்பொறிகள் ஒரே சீரானவையாக இருக்கவேண்டுமென்பதில்லை என்றாலும் அவ்வாறு இல்லாவிட்டால் சுமை சமன்படுத்துதல் மிகக் கடினமானதாக இருக்கும். மிகவும் பொது வகையான கொத்தாக இருப்பது பியோவுல்ஃப் கிளஸ்டர், இது TCP/IP ஈத்தர்நெட் குறும்பரப்புப் பிணையத்துடன் இணைக்கப்பட்ட பன்மடங்கு ஒத்த வர்த்தகரீதியான காட்சிக்கு இல்லாத கணினிகளில் நடைமுறைப்படுத்தப்பட்ட கொத்தாகும்.[27] பியோவுல்ஃப் தொழில்நுட்பம் முதன் முதலில் தாமஸ் ஸ்டெர்லிங் மற்றும் டோனால்ட் பெக்கர் ஆகியோரால் உருவாக்கப்பட்டது. மிகப் பெரும்பான்மையான சிறந்த 500 சூப்பர்கணிப்பொறிகள் கிளஸ்டர்களாக இருக்கிறது.[28]
பெருத்த இணைச் செயலாக்கம்[தொகு]
பெருத்த இணை செயலி (MPP) என்பது பல வலையமைப்புகளுடைய செயலிகளைக் கொண்ட ஒரு ஒற்றைக் கணினியாகும். பெருத்த இணை செயலிகள் கிளஸ்டர்களைப் போலவே அதே பண்புக்கூறுகளைக் கொண்டிருக்கின்றன, ஆனால் பெருத்த இணை செயலிகள் தனித்துவ சேர்த்திணைத்த வலையமைப்பைக் கொண்டிருக்கின்றன (ஆனால் கிளஸ்டர்களோ வலையமைப்புக்குப் பண்ட வன்பொருளைப் பயன்படுத்துகின்றன). பெருத்த இணைச் செயலிகள் கிளஸ்டர்களைக் காட்டிலும் பெரிதாக இருப்பதாகத் தோன்றுகிறது, வழக்கமாக 100 செயலிகளுக்கும் "மிக அதிகமாக" கொண்டிருக்கிறது.[29] ஒரு பெருத்த இணைச் செயலியில் "ஒவ்வொரு மையச் செயலகமும் தனதே ஆன நினைவகம் மற்றும் இயங்குதள அமைப்பு மற்றும் பயன்பாடுகளின் ஒரு பிரதியையும் கொண்டிருக்கிறது. ஒவ்வொரு உபஅமைப்பும் மற்றவற்றுடன் ஒரு உயர் வேக சேர்த்திணைப்பு மூலம் தகவல்தொடர்பு கொள்கிறது."[30]

ஜூன் 2009 சிறந்த 500 தரவரிசைப்பட்டியலின் கூற்றுப்படி உலகின் மிக வேகமான ஐந்தாவது சூப்பர் கம்ப்யூட்டரான புளூ ஜீன்/எல், ஒரு பெருத்த இணை செயலியாகும்.
கிரிட் கணிப்பீடு[தொகு]
கிரிட் கணிப்பீடுதான் இணைக் கணிப்பீடின் மிகவும் பரவிய வடிவமாக இருக்கிறது. கொடுக்கப்பட்டுள்ள ஒரு கணக்கின் மீது பணிசெய்ய இது இணையத்தில் தகவல்தொடர்பு கொள்ளும் கணினிகளைப் பயன்படுத்திக்கொள்கிறது. இணையத்தில் கிடைக்கப்பெறும் குறைந்த பட்டைஅகலம் மற்றும் மிகவும் உயர்ந்த மறைநிலை காரணமாக கிரிட் கணிப்பீடு வகைமாதிரியாக இக்கட்டான இணை கணக்குகளை மட்டுமே எதிர்கொள்கிறது. பல கிரிட் கணிப்பீடு பயன்பாடுகள் உருவாக்கப்பட்டுள்ளது, அவற்றுள் SETI@home மற்றும் Folding@Home ஆகியவை மிகவும் பிரபலமாக இருக்கும் எடுத்துக்காட்டுகளாகும்.[31]
பெரும்பாலான கிரிட் கணிப்பீட்டு பயன்பாடுகள் இடைப்பொருள்-ஐப் பயன்படுத்துகின்றன, வலையமைப்பு ஆதாரங்களை நிர்வகிப்பதற்கும் மென்பொருள் இடைமுகத்தை நிர்ணயப்படுத்துவதற்கும் இயங்குதள அமைப்பு மற்றும் பயன்பாடுகளுக்கு இடையில் வீற்றிருக்கும் ஒரு மென்பொருள். மிகப் பொதுவாகக் காணப்படும் கிரிட் கணிப்பீட்டு இடைப்பொருளாக இருப்பது பெர்க்கெலி ஓப்பன் இன்ஃப்ராஸ்டரக்சர் ஃபார் நெட்வர்க் கம்ப்யூடிங் (BOINC). கிரிட் கணிப்பீட்டு மென்பொருள் அடிக்கடி "கூடுதல் சுழற்சி"களைப் பயன்படுத்திக் கொள்கிறது, இது கணிப்பொறி வெறுமனே இருக்கும் நேரங்களில் கணிப்பீடுகளைச் செய்விக்கிறது.
தனித்துவ இணை கணினிகள்[தொகு]
இணைக் கணிப்பீடுகளுக்குள்ளாகவே, தகுதிவாய்ந்த ஆர்வம் ஏற்படுத்தக்கூடியவையாகவே இருக்கும் தனித்துவ இணை சாதனங்கள் இருக்கின்றன. அவை திரளம்-குறித்தவையாக இல்லாதபோதும், அவை இணைக் கணக்குகளின் சில பிரிவுகளுக்கு மட்டுமே பொருந்தும் போக்கினைக் கொண்டிருக்கின்றன.
புல நிரல்தகு வாயில் அடுக்குடன் கூடிய மீண்டும் உருவாக்கப்படும் கணிப்பீடு[தொகு]
மீண்டும் உருவாக்கக்கூடிய கணிப்பீடு என்பது ஒரு பொது-பயன்பாடு கணிப்பொறிக்கு ஒரு உடன்-செயலியாக புல நிரல்தகு வாயில் அடுக்கு (FPGA) பயன்படுகிறது. புல நிரல்தகு வாயில் அடுக்கு என்பது, சுருக்கமாக, ஒரு கொடுக்கப்பட்ட பணிக்கு தனக்குத்தானே மீண்டும் கம்பியிட்டுக் கொள்ளும் ஒரு கணினி சில்லாகும்.
புல நிரல்தகு வாயில் அடுக்குகள், VHDL அல்லது Verilog போன்ற வன்பொருள் விவரிப்பு மொழிகளால் நிரலாக்கப்படலாம். எனினும் இந்த மொழிகளில் நிரலாக்கம் செய்வது சோர்வூட்டுகிறதாக அமையலாம். பெரும்பாலான நிரலொழுங்கு ஆயத்தச் செயலர்களுக்குப் பரிச்சயமாக இருக்கும் C நிரலாக்க மொழியின் வழிமுறைத் தொடரமைப்பு மற்றும்/அல்லது சொற்பொருளியலுக்கு சமமாக இருக்க முயற்சிக்கும் C முதல் HDL வரையிலான மொழிகளை பல்வேறு விற்பனையாளர்கள் உருவாக்கியுள்ளனர். மிகவும் பிரபலமாக அறியப்பட்ட C முதல் HDL வரையிலான மொழிகளாக இருப்பவை மிட்ரியான்-C, இம்பல்ஸ் C, DIME-C மற்றும் ஹாண்டெல்-C. C++ ஐ அடிப்படையாகக் கொண்டு SystemC யின் குறிப்பிட்ட உட்கணங்களும் கூட இதற்காகப் பயன்படுத்தப்படலாம்.
தன்னுடைய ஹைபர்டிரான்ஸ்போர்ட் தொழில்நுட்பத்தை மூன்றாம் தரப்பு விற்பனையாளர்களிடம் கொண்டுசெல்லும் AMD யின் முடிவு, உயர்செயல்பாட்டு மீண்டும் உருவாக்கக்கூடிய கணிப்பீட்டுக்கான ஆற்றல்மிகு தொழில்நுட்பமாக உருவாகியிருக்கிறது.[32] டீஆர்சி கம்ப்யூட்டர் கார்ப்போரேஷன், முதன்மை இயக்க அதிகாரியான மைக்கல் ஆர். டி அமோர் இவ்வாறு கூறினார், "நாங்கள் AMD க்குள் முதன் முதலாக நுழைந்தபோது அவர்கள் எங்களை 'பொருத்துவாய் (socket) திருடர்கள்' என்று அழைத்தனர். இப்போது அவர்கள் எங்களைக் கூட்டாளிகள் என்று அழைக்கின்றனர்."[32]
வரைகலை செயல்முறை அலகு மீதான பொதுப் பயன் கணிப்பீடு (GPGPU)[தொகு]

வரைகலை செயல்முறை அலகுகளின் மீதான பொதுப் பயன் கணிப்பீடு (GPGPU) என்பது கணினி பொறியியல் ஆராய்ச்சியில் மிகச் சமீபத்திய போக்காகும். வரைகலை செயல்முறை அலகுகள் என்பவை கணினி வரைகலை செயல்முறையாக்கங்களுக்காகப் பெரிதும் உகப்பாக்கப்பட்டிருக்கும் கூட்டு செயலிகளாகும்.[33] கணினி வரைகலை செயல்முறையாக்கம் என்பது தரவு இணை இயக்கங்களால் ஆதிக்கம் செலுத்தப்பெறும் ஒரு துறையாகும், குறிப்பாக நேரியல் இயற்கணித அணி இயக்கங்களில்.
ஆரம்ப நாட்களில் நிரல்களைச் செயல்படுத்துவதற்கு, வரைகலை செயல்முறை அலகுகளின் மீதான பொதுப் பயன் கணிப்பீட்டு நிரல்கள் சாதாரணமான வரைகலை API களைப் பயன்படுத்தின. எனினும் சமீப காலங்களில் வரைகலை செயல்முறை அலகுகளில் பொதுப் பயன் கணிப்பீடுகளைச் செய்வதற்குப் பல்வேறு புதிய நிரலாக்க மொழிகள் மற்றும் இயக்குதளங்கள் கட்டப்பட்டுள்ளன, இதில் நிவிடியா மற்றும் AMD முறையே CUDA மற்றும் CTM உடன் நிரலாக்கச் சூழல்களை வெளியிட்டுள்ளன. இதர வரைகலை செயல்முறை அலகு நிரலாக்க மொழிகளாக இருப்பவை புரூக் ஜிபியூ, பீக்ஸ்ட்ரீம் மற்றும் ராபிட்மைண்ட். தங்களுடைய தொஸ்லா தொடர்களில் கணிப்பீடு செய்வதற்கு நிவிடியா குறிப்பிட்ட உற்பத்திப்பொருட்களையும் கூட வெளியிட்டது.
குறித்த பயன்பாட்டு ஒருங்கிணைந்த மின்சுற்று[தொகு]
இணை பயன்பாடுகளுடன் கையாளக்கூடிய பல்வேறு குறித்த பயன்பாட்டு ஒருங்கிணைந்த மின்சுற்று (ASIC) அணுகுமுறைகள் உருவாக்கப்பட்டுள்ளது.[34][35][36]
ஒரு குறித்த பயன்பாட்டு ஒருங்கிணைந்த மின்சுற்று கொடுக்கப்பட்ட ஒரு பயன்பாட்டுக்குக் குறித்ததாக இருப்பதால், அது அந்த பயன்பாட்டிற்கு முழுமையாக உகப்பாக்கப்படலாம். இதன் விளைவாக ஒரு கொடுக்கப்பட்ட பயன்பாட்டுக்கு, குறித்த பயன்பாட்டு ஒருங்கிணைந்த மின்சுற்று ஒரு பொதுப்-பயன் கணினியை விஞ்சிவிட முயல்கிறது. எனினும் குறித்த பயன்பாட்டு ஒருங்கிணைந்த மின்சுற்றுகள் ஊடு கதிர் பதிவச்சுக் கலை மூலம் உருவாக்கப்படுகிறது. இந்தச் செயல்முறைக்கு ஒரு மறைப்பு தேவைப்படுகிறது அது மிகவும் விலையுயர்ந்தவையாக இருக்கலாம். ஒரு ஒற்றை மறைப்பு ஒரு மில்லியன் அமெரிக்க டாலருக்கும் அதிகமாக இருக்கலாம்.[37] (சில்லுக்கு தேவையான டிரான்சிஸ்டர் எவ்வளவு சிறியதாக இருக்கிறதோ, அவ்வளவுக்கு மறைப்பின் விலையும் அதிகரித்துக் கொண்டே இருக்கும்.) அதே நேரத்தில், காலப்போக்கில் பொது-பயன் கணிப்பீடுகளில் செயல்பாடுகளின் அதிகரிப்பு (மூரின் விதிமுறையில் விவரிக்கப்பட்டுள்ளது போல) ஒன்று அல்லது இரண்டு சில்லு தலைமுறைகளில் மட்டும் இந்தப் பலன்களை அழித்துவிட முனைகிறது.[32] உயர்ந்த ஆரம்பக்கட்ட செலவினங்கள் மற்றும் மூரின் விதிமுறையால் உந்தப்பட்ட பொதுப்-பயன் கணிப்பீட்டினால் தடம் மாறும் போக்கு ஆகியவற்றால் பெரும்பாலான இணைக் கணிப்பீடு பயன்பாடுகளுக்கு, குறித்த பயன்பாட்டு ஒருங்கிணைந்த மின்சுற்று இயலாததாக ஆக்கிவிடுகிறது. எனினும், சில கட்டப்பட்டுள்ளன. ஓர் உதாரணமாக இருப்பது பெடா-தோல்வியான RIKEN MDGRAPE-3 கணினி இது மூலக்கூறு இயக்கவியல் உருவகப்படுத்தலுக்கு வாடிக்கையான குறித்த பயன்பாட்டு ஒருங்கிணைந்த மின்சுற்றைப் பயன்படுத்துகிறது.
திசையன் செயலிகள்[தொகு]

ஒரு திசையன் செயலி என்பது ஒரு மையச் செயலகம் அல்லது கணிப்பொறி அமைப்பாகும், இது பெரும் தொகுப்பு தரவுகளில் அதே நெறிமுறைகளைச் செயல்படுத்தக்கூடும். "திசையன் செயலிகள், எண்கள் அல்லது திசையன்களின் நேரியல் அலைவாங்கி வரிசைகளில் வேலைசெய்யக்கூடிய உயர்-நிலை இயக்கங்களைக் கொண்டிருக்கின்றன. திசையன் இயக்கத்தின் ஒரு எடுத்துக்காட்டு A = B × C , இங்கு A , B மற்றும் C ஒவ்வொன்றும் 64-நுண்ம மிதவைப் புள்ளி எண்களின் 64-கூறு திசையன்களாகும்."[38] அவை ஃப்ளையன்னின் SIMD வகைப்பாட்டுக்கு மிக நெருக்கமாகத் தொடர்பு கொண்டுள்ளன.[38]
கிரே கணினிகள் தங்களுடைய திசையன்-செயல்முறையாக்க கணினிகளுக்காக 1970 மற்றும் 1980 ஆம் ஆண்டுகளில் பிரபலமடைந்தன. எனினும் திசையன் செயலிகள் — மைய செயலகம் மற்றும் முழு கணிப்பொறி அமைப்பு என இருவகையிலுமே பொதுவாகக் காணாமல்போய்விட்டது. நவீன செயலி நெறிமுறைத் தொகுப்புகள், AltiVec மற்றும் ஸ்ட்ரீமிங் SIMD எக்ஸ்டன்ஷன்ஸ் (SSE) போன்ற சில திசையன் செயல்முறையாக்க நெறிமுறைகளைச் சேர்த்துக்கொண்டுள்ளன.
மென்பொருள்[தொகு]
இணை நிரலாக்க மொழிகள்[தொகு]
ஒருங்கிசையும் நிரலாக்க மொழிகள், நூலகங்கள், ஏபிஐகள் மற்றும் இணை நிரலாக்க மாதிரிகள் (படித்தீர்வுக்குரிய கட்டமைப்பு போன்றவை) நிரலாக்க இணை கணினிகளுக்காக உருவாக்கப்பட்டுள்ளது. பகிர்ந்த நினைவகம், பரவிய நினைவகம் அல்லது பகிர்ந்து பரவிய நினைவகம் என நினைவக கட்டமைப்பின் ஆதாரத்தின் மீது அவை ஊகம் செய்வதை அடிப்படையாகக் கொண்டு இவை பொதுவாக பிரிவுகளாகப் பிரிக்கப்படலாம். பகிர்ந்த நினைவக நிரலாக்க மொழிகள் பகிர்ந்த நினைவக மாறும் தன்மையுடையவற்றைக் கையாள்வதன் மூலம் தகவல்தொடர்பு கொள்கின்றன. பரவிய நினைவகம் தகவல் அனுப்புதலைப் பயன்படுத்துகிறது. POSIX திரிகள் மற்றும் OpenMP ஆகிய இரண்டும் மிகவும் பரவலாகப் பயன்படுத்தப்படும் பகிர்ந்த நினைவக API களாகும், அதேசமயம் தகவல் அனுப்பும் இடைமுகம் (MPI) தான் மிகவும் பரவலாகப் பயன்படுத்தப்பட்டும் தகவல் அனுப்பும் அமைப்பு API ஆகும்.[39] நிரலாக்கப்படும் இணை நிரல்களில் பயன்படுத்தப்படும் ஒரு கருத்துப் படிவமாக இருப்பது எதிர்கால கருத்துப்படிவம், இங்கு நிரலின் ஒரு பாகம் நிரலின் மற்றொரு பாகத்திற்குத் தேவைப்படும் செய்திக் குறிப்பை எதிர்காலத்தில் எப்போதாவது அனுப்பிவைப்பதாக உறுதியளிக்கிறது.
தன்னியக்க இணைச் செயற்படுத்தல்[தொகு]
இருமமாக்கியால் ஒரு வரிசைமுறையிலான நிரலின் தன்னியக்க இணைச் செயற்படுத்தப்படுவது என்பது இணைக் கணிப்பீட்டின் புனித புத்தகமாகும். இருமமாக்கி ஆராய்ச்சியாளர்கள் பல ஆண்டுகள் பணி மேற்கொண்டபோதிலும் தன்னியக்க இணைச் செயற்படுத்தல் குறைந்த வெற்றியையே கொண்டிருக்கிறது.[40]
முதன்மை இணை நிரலாக்க மொழிகள், திட்டவட்டமான இணை அல்லது (பொருந்தும்வகையில்) சிறிதளவே உள்ளார்ந்தவை என எதுவாகவும் இருக்கலாம், இங்கு ஒரு நிரலர் இணைச் செயற்படுத்தலுக்கான கட்டளைகளை இருமமாக்கிக்கு வழங்குகிறது. முழுமையாக உள்ளார்ந்தைவையாக இருக்கும் சில இணை நிரலாக்க மொழிகளும் இருக்கின்றன —SISAL, பாரலல் ஹாஸ்கெல் மற்றும் (FPGAக்களுக்கு) மிட்ரியான்-C.
பயன்பாடு சோதனை செய்தல்[தொகு]
ஒரு கணிப்பொறி எவ்வளவக்கெவ்வளவு பெரிதாகவும் சிக்கலானதாகவும் இருக்கிறதோ அந்த அளவுக்கு அதன் பழுதடையும் தன்மையும் அதிகரிக்கும் மற்றும் தோல்விகளுக்கிடையிலான சராசரி நேரம் குறைவாகவே இருக்கும். பயன்பாடு சோதனை செய்தல் என்னும் உத்தி மூலம் கணிப்பொறி அமைப்பு பயன்பாட்டினை ஒரு "நொடிப்பு நிழற்படமெடுக்கிறது" - தற்போதைய அனைத்து ஆதார ஒதுக்கீடுகள் மற்றும் மாற்றம்கொள்ளக்கூடிய நிலைகளின் ஒரு பதிவு ஆகும் இது ஒரு உள்ளார்ந்த கொட்டிடம் போன்றதாகும்; கணிப்பொறி தோல்வியுறும் பட்சத்தில் நிரலை மீட்டெடுக்க இந்த தகவல் பயன்படுத்தப்படலாம். பயன்பாடு சோதனை செய்தல் என்றால் நிரல் ஆரம்பத்திலிருந்து தொடங்குவதற்குப் பதிலாக தன்னுடைய கடைசி பரிசோதனை இடத்திலிருந்து மட்டுமே மீண்டும் தொடங்கலாம் என்று பொருள். பல மாதங்களுக்கு இயங்கக்கூடிய ஒரு பயன்பாட்டிற்கு இது முக்கியமானதாகும். செய்முறை குடிபெயர்தலை எளிமைப்படுத்துவதற்குப் பயன்பாட்டு சோதனை செய்தல் பயன்படுத்தப்படலாம்.
படித்தீர்வுக்குரிய வழிமுறைகள்[தொகு]
இணை கணினிகள் பெரியதாகவும் வேகமாகவும் ஆகவும், முன்னர் இயங்குவதற்கு நீண்ட நேரம் எடுத்துக்கொண்ட கணக்குகளைத் தீர்ப்பது சாத்தியமானது. இணை கணிப்பீடு பல புலங்களில் பயன்படுத்தப்படுகிறது, அவை உயிரித்தகவலியல் (புரத மடிப்புகள்) முதல் பொருளாதாரம் (கணக்கியல் நிதி) வரையில் பரந்து விரிந்து இருக்கிறது. இணைக் கணிப்பீட்டு பயன்பாடுகளில் காணப்படும் மிகப் பொதுவான வகை கணக்குகள்:[41]
- அடர்த்தியான நேரியல் இயற்கணிதம்
- அடர்த்தியற்ற நேரியல் இயற்கணிதம்
- அலைமாலை வழிமுறைகள் (கூலே-டூகீ வேக ஃபோரியர் உருமாற்றம் போன்றவை)
- n -கட்டமைப்பு கணக்குகள் (பார்னெஸ்-ஹட் உருவகப்படுத்தல் போன்றவை)
- வடிவமைக்கப்பட்ட கிரிட் கணக்குகள் (லாட்டிஸ் போல்ட்ஸ்மான் வழிமுறைகள் போன்றவை)
- வடிவமைக்கப்படாத கிரிட் கணக்குகள் (குருகணுபகுப்பாய்வில் காணப்படுவது போன்றவை)
- மான்டே கார்லோ உருவகப்படுத்தல்
- சேர்மானத்துக்குரிய ஏரணம் (முரட்டு மறையீட்டு நுட்பம் போன்றவை)
- வரைபட குறுக்குகோடு (படித்தீர்வுகள் வகைப்பிரிப்பு போன்றவை)
- செயல்மிகு நிரலாக்கம்
- கிளைவிடுதல் மற்றும் இணைதல் வழிமுறைகள்
- வரைகலைக்குரிய மாதிரிகள் (மறைந்திருக்கும் மார்கோவ் மாதிரிகளைக் கண்டறிதல் மற்றும் பேயிசியான் வலையமைப்புகளைக் கட்டுதல் போன்றவை)
- முடிவுள்ள-நிலை கணிப்பொறி உருவகப்படுத்தல்
வரலாறு[தொகு]

உண்மையான (MIMD) இணைச் செயற்பாடுகளின் மூலங்கள் ஃபெடிரிகோ லூய்கி, கோண்டே மொனாபிரியா மற்றும் அவருடைய "சார்லஸ் பாப்பேஜ் அவர்களால் கண்டுபிடிக்கப்பட்ட பகுப்புமுறை பொறியின் மேலோட்ட திட்டம்" ஆகியவற்றை எட்டுகிறது.[42][43] 1954 ஆம் ஆண்டில் ஐபிஎம், ஜீன் அம்தால் முதன்மை கட்டுமானர்களில் ஒருவராக இருந்த ஒரு செயல்திட்டத்தின் மூலம் 704-ஐ அறிமுகப்படுத்தியது. முழுமையாக தானியங்கி மிதவைப் புள்ளி கணக்கியல் கட்டளையைப் பயன்படுத்தும் வர்த்தகரீதியாக கிடைக்கப்பெறும் முதல் கணினியாக ஆனது.[44]
1958 ஆம் ஆண்டு ஏப்ரலில், எஸ்.கில் (ஃபெர்ரான்டி) அவர்கள் இணை நிரலாக்கம் மற்றும் கிளைப்படுத்தி காத்திருத்தலின் தேவையைப் பற்றி விவாதித்தார்.[45] மேலும் 1958 ஆம் ஆண்டிலேயே, ஐபிஎம் ஆராய்ச்சியாளர்கள் ஜான் கோகெ மற்றும் டேனியல் ஸ்லாட்நிக் ஆகியோர் எண்கணித கணிப்பீடுகளில் இணைச் செயற்பாடுகளின் பயன்பாட்டை முதன் முதலாக விவாதித்தனர்.[46] 1962 ஆம் ஆண்டில் பர்ரோக்ஸ் கார்ப்போரேஷன் D825 ஐ அறிமுகப்படுத்தியது, நான்கு செயலி கணினியான இது குறுக்குத்தண்டு இணைப்புமாற்றி மூலம் 16 நினைவக நிரல்கூறுகள் வரை அணுக்கம் செய்தது.[47] 1967 ஆம் ஆண்டில் அம்தால் மற்றும் ஸ்லாட்னிக், தகவல் செயல்பாட்டு அமைப்புகளின் அமெரிக்க கூட்டமைப்பு மாநாட்டில் இணை செயல்பாட்டு சாத்தியம் பற்றிய ஒரு வாதத்தை வெளியிட்டனர்.[46] இந்த வாதத்தின் போதுதான் இணைச் செயற்பாடு காரணமாக வேகப்படுத்துதலின் எல்லையை வரையறுப்பதற்கான அம்தாலின் விதிமுறை உருவகப்படுத்தப்பட்டது.
1969 ஆம் ஆண்டில் அமெரிக்க நிறுவனமான ஹனிவெல் தன்னுடைய முதல் மல்டிக்ஸ் கணினியை அறிமுகப்படுத்தியது, இது இணையில் எட்டு செயலிகள் வரையில் இயக்கச் செய்யும் திறன் கொண்ட சமச்சீருடைய பன்மடங்குசெயலி அமைப்பாகும்.[46] கார்னெஜீ மெல்லான் பல்கலைக்கழகத்தில் 1970 ஆம் ஆண்டுகளில் பன்மடங்கு-செயலி செயல்திட்டமான C.mmp, "ஒரு சில செயலிகளுக்கும் மேலாகக் கொண்டிருக்கும் பன்மடங்குசெயலிகளில் முதன்மையானவைகளில் ஒன்றாகும்".[43] "தலையிடக்கூடிய சேமிப்பகத்துடன் முதல் பாட்டை-இணைக்கப்பட்ட பன்மடங்கு-செயலியாக இருந்தது 1984 ஆம் ஆண்டின் சைநாப்சே N+1."[43]
SIMD இணை கணினிகள் 1970 ஆம் ஆண்டுகளுக்கு முந்தி வரை அடையாளங்காணமுடியும். ஆரம்பகால SIMD கணினிகளுக்கான உந்துகோலாக இருந்தது பன்மடங்கு நெறிமுறைகளையும் மீறி செயலியின் கட்டுப்பாட்டு கூறுகளின் வெளி தாமதத்தைத் தீர்ப்பதாகும்.[48] 1964 ஆம் ஆண்டில், லாரன்ஸ் லிவர்மோர் தேசிய பரிசோதனைக் கூடம் ஸ்லாட்நிக் ஒரு மிகப்பெரும் இணை கணிப்பொறியைக் கட்டுவதற்குப் பரிந்துரை செய்தார்.[46] அவருடைய வடிவமைப்பு அமெரிக்க வான் படையால் நிதியாதாரம் செய்யப்பட்டது, இது தான் ஆரம்பகால SIMD இணை-கணீப்பீட்டு முயற்சி ILLIAC IV ஆகும்.[46] அதன் வடிவமைப்பிற்கான முக்கிய விஷயமாக இருப்பது 256 செயலிகளுடன் கூடிய மிகவும் உயர்ந்த இணைச் செயற்பாடு, இது பெரும் தரவுதொகுப்புகளில் கணினியைப் பணி செய்ய அனுமதித்தது, பின்னாளில் அது வரைகலை செயல்முறையாக்கம் என அறியப்படலாயிற்று. எனினும் ILLIAC IV "சூப்பர் கணிப்பொறிகளில் மிகவும் இகழ்ச்சிக்குரியது" என அழைக்கப்பட்டது, ஏனெனில் அந்த செயல்திட்டம் வெறும் கால்பாகம் மட்டுமே நிறைவடைந்திருந்தது ஆனால் அது 11 ஆண்டுகள் எடுத்துக்கொண்டதுடன் முதலில் மதிப்பீடு செய்யப்பட்ட தொகையைவிட கிட்டத்தட்ட நான்கு மடங்கு அதிகரித்தது.[49] 1976 ஆம் ஆண்டில் அது தன்னுடைய முதல் நிஜ பயன்பாட்டினை இயக்க இறுதியாகத் தயாரானபோது க்ரே-1 போன்ற வர்த்தரீதியான சூப்பர்கணிப்பொறிகளால் அது விஞ்சப்பட்டது.
இவற்றையும் பார்க்கவும்[தொகு]
- உடன்நிகழ்வு, இணை மற்றும் பகிர்வு கணிப்பீடுகளில் முக்கிய வெளியீடுகளின் பட்டியல்
- பரவிய கணிப்பீடு மாநாடுகளின் பட்டியல்
- உள்ளடக்கம் முகவரியிடத்தகும் இணைச் செயலி
குறிப்புதவிகள்[தொகு]
- ↑ அல்மாசி, ஜி.எஸ். மற்றும் ஏ. காட்லீய்ப் (1989). ஹைலி பாரலல் கம்ப்யூடிங் . பென்ஜமின்-கம்மிங்க்ஸ் வெளியீட்டாளர்கள், ரெட்வுட் சிட்டி, சிஏ.
- ↑ எஸ்.வி. அட்வே மற்றும் பலர். நவம்பர் 2008 "பாரலல் கம்ப்யூடிங் ரிசர்ச் அட் இல்லினாய்ஸ்: தி யூபிசிஆர்சி அஜெண்டா" பரணிடப்பட்டது 2008-12-09 at the வந்தவழி இயந்திரம் (பிடீஎஃப்). Parallel@Illinois, யூனிவெர்சிடி ஆஃப் இல்லினாய்ஸ் அட் உர்பானா-காம்பேய்ன். "அதிகரித்த கடிகார அலைவெண் மற்றும் சாதுர்யமிக்க ஆனால் அதிகரித்துவரும் கடின கட்டுமானங்களைக் கொண்ட இந்தச் செயல்திறன் ஆதாயங்களின் முக்கிய தொழில்நுட்பங்கள் இப்போது ஆற்றல் தடைகள் என அழைக்கப்படுபவைகளைத் தகர்க்கின்றன. எதிர்கால செயல்திறன் அதிகரிப்புகள் பெருவாரியாக ஒரு வகுமத்தின் செயலிகளின் (அல்லது உள்மையப் பகுதிகள்) எண்ணிக்கையை அதிகரிப்பதன் மூலம் வரவேண்டுமே தவிர ஒரு ஒற்றை உள்மையப் பகுதியை வேகமாக்குவதன் மூலம் அல்ல என்பதை கணினித் தொழில்துறை ஒப்புக்கொண்டுள்ளது."
- ↑ அசாநோவிக் மற்றும் பலர். பழைய [ஏற்றுக்கொள்ளப்பட்ட மதிநுட்பம்]: மின்ஆற்றல் இலவசமானது ஆனால் டிரான்சிஸ்டர்கள் விலையுயர்ந்தவை. புதிய [ஏற்றுக்கொள்ளப்பட்ட மதிநுட்பம்] மின்ஆற்றல் விலையுயர்ந்தவை ஆனால் டிரான்சிஸ்டர்கள் "கட்டுப்பாடுகளற்று" இருக்கின்றன.
- ↑ அசானோவில், க்ரிஸ்டே மற்றும் பலர். திசம்பர் 18, 2006. "தி லாண்ட்ஸ்கேப் ஆஃப் பாரலல் கம்ப்யூடிங் ரிசர்ச்: எ வியூ ஃப்ரம் பெர்கெலி" (பிடீஎஃப்). கலிபோர்னியா பல்கலைக்கழகம், பெர்கெலி. தொழில்நுட்ப அறிக்கை எண். UCB/EECS-2006-183. "பழைய [ஏற்றுக்கொள்ளப்பட்ட மதிநுட்பம்]: செயலி செயல்திறனை மேம்படுத்துவதில் முதன்மை வழிமுறையாக இருப்பது கடிகார அலைவெண்ணை அதிகரிப்பதாகும். பழைய [ஏற்றுக்கொள்ளப்பட்ட மதிநுட்பம்]: செயலி செயல்திறனை மேம்படுத்துவதில் முதன்மை வழிமுறையாக இருப்பது இணைச் செயற்பாட்டை அதிகரிப்பதாகும்... 'அதிக கடிகார வேகம் மேம்பாடுடையது' என்னும் நிலையுடன் பொதுவாகத் தொடர்புடைய நிறுவனமான இன்டெல்லின் பிரதிநிகளும் கூட, கடிகார வேகத்தை அதிகரிப்பதன் மூலம் செயல்திறனை அதிகபட்சமாக்கும் என்னும் பாரம்பரியமிக்க அணுகுமுறைகள் அவற்றின் எல்லைகளுக்கு தள்ளப்பட்டிருக்கிறது என்று எச்சரித்துள்ளனர்."
- ↑ பாட்டர்சன், டேவிட் ஏ. மற்றும் ஜான் எல். ஹென்னெச்சி (1998). கம்ப்யூட்டர் ஆர்கனைசேஷன் அண்ட் டிசைன் , இரண்டாவது பதிப்பு, மோர்கன் கோஃப்மான் வெளியீட்டாளர்கள், ப. 715. ஐஎஸ்பிஎன் 1558604286
- ↑ 6.0 6.1 Barney, Blaise. "Introduction to Parallel Computing". Lawrence Livermore National Laboratory. Archived from the original on 2013-06-29. பார்க்கப்பட்ட நாள் 2007-11-09.
- ↑ ஹென்னெச்சி, ஜான் எல். மற்றும் டேவிட் ஏ. பாட்டர்சன் (2002). கம்ப்யூட்டர் அப்ரோச்: எ குவான்டிடேடிவ் அப்ரோச் . மூன்றாவது பதிப்பு, மோர்கன் கோஃப்மான், ப. 43. ஐஎஸ்பிஎன் 1558607242.
- ↑ ராபேய், ஜெ. எம். (1996). டிஜிடல் இன்டிகிரேடெட் சர்க்யூட்ஸ் . பிரென்டைஸ் ஹால், ப. 235. ஐஎஸ்பிஎன் 0131786091.
- ↑ ஃப்ளைன், லௌரீ ஜெ. "இன்டெல் ஹால்ட்ஸ் டெவலப்மெண்ட் ஆஃப் டூ நியூ மைக்ரோபுரோசெசர்ஸ்". தி நியூ யார்க் டைம்ஸ், மே 8, 2004. ஏப்ரல் 22, 2008 அன்று மீட்டெடுக்கப்பட்டது.
- ↑ Moore, Gordon E. (1965). "Cramming more components onto integrated circuits" (PDF). Electronics Magazine. p. 4. Archived from the original (PDF) on 2008-02-18. பார்க்கப்பட்ட நாள் 2006-11-11.
- ↑ அம்தால், ஜி. (ஏப்ரல் 1967) "தி வேலிடிடி ஆஃப் தி சிங்கள் புரோசெசர் அப்ரோச் டு அசீவிங் லார்ஜ் ஸ்கேல் கம்ப்யூடிங் கேபபிலிடிஸ்". புரொசீடிங்க்ஸ் ஆஃப் AFIPS ஸ்ப்ரிங் ஜாய்ண்ட் கம்ப்யூட்டர் கான்ஃபரன்ஸ் இல், அட்லாண்டிக் நகரம், நியூ.ஜெர்சி., AFIPS பிரஸ், பக். 483–85.
- ↑ புரூக்ஸ், ஃப்ரெட்ரிக் பி. ஜூனியர். தி மைதிக்கல் மான்-மந்த்: எஸ்ஸேஸ் ஆன் சாஃப்ட்வேர் என்ஜினியரிங். . அத்தியாயம் 2 – தி மைதிக்கல் மான்-மந்த். ஐஎஸ்பிஎன் 0201835959
- ↑ ரீஇவாலுவேடிங் அம்தால்ஸ் லா பரணிடப்பட்டது 2012-06-23 at the வந்தவழி இயந்திரம் (1988). கம்யூனிகேஷன்ஸ் ஆஃப் தி ஏசிஎம் 31(5), பக். 532–33.
- ↑ பெர்ன்ஸ்டீய்ன், ஏ. ஜெ. (அக்டோபர் 1966). "புரோகிராம் அனாலிசஸ் ஃபார் பாரலல் புரோசெசிங்,' IEEE டிரான்சாக்ஷன்ஸ் ஆன் எலக்ட்ரானிக் கம்ப்யூட்டர்ஸ்". EC-15, பக். 757–62.
- ↑ ரூஸ்டா, சீயெட் எச். (2000.) "பாரலல் புரோசெசிங் அண்ட் பாரலல் அல்கோரிதம்ஸ்: தியரி அண்ட் கம்பூடெஷன்". ஸ்ப்ரிங்கர், ப. 114. ஐஎஸ்பிஎன் 0387987169.
- ↑ லாம்போர்ட், லெஸ்லீ (செப்டம்பர் 1979). "ஹௌ டு மேக் எ மல்டிபுரோசஸர் கம்ப்யூட்டர் தட் கரெக்ட்லி எக்சிகியூட்ஸ் மல்டிபுரோசெஸ் புரோகிராம்ஸ்", IEEE டிரான்சாக்ஷன்ஸ் ஆன் கம்ப்யூட்டர்ஸ், C-28,9, பக். 690–91.
- ↑ பாட்டர்சன் மற்றும் ஹென்னெச்சி, ப. 748.
- ↑ கல்லர், டேவிட் இ.; ஜஸ்விந்தர் பால் சிங் மற்றும் அனூப் குப்தா (1999). பாரலல் கம்ப்யூட்டர் ஆர்கிடெக்சர் - எ ஹார்ட்வேர்/சாஃப்ட்வேர் அப்ரோச் . மோர்கன் கோஃப்மான் வெளியீட்டாளர்கள், ப. 15. ஐஎஸ்பிஎன் 1558603433.
- ↑ கல்லர் மற்றும் பலர். ப. 15.
- ↑ பாட், யேல் (ஏப்ரல் 2004). "தி மைக்ரோபுரோச்செர் டென் இயர்ஸ் ஃப்ரம் நௌ: வாட் ஆர் தி சேலஞ்ஜஸ், ஹௌ டு வி மீட் தெம்? (wmv). கார்னேஜி மெல்லான் பல்கலைக்கழகத்தில் மதிப்புமிக்க பேராசிரியரின் உரை. நவம்பர் 7, 2007 அன்று மீட்டெடுக்கப்பட்டது.
- ↑ 21.0 21.1 கல்லர் மற்றும் பலர். ப. 124.
- ↑ 22.0 22.1 கல்லர் மற்றும் பலர். ப. 125.
- ↑ 23.0 23.1 பாட்டர்சன் மற்றும் ஹென்னெச்சி, ப. 713.
- ↑ 24.0 24.1 ஹென்னெச்சி மற்றும் பாட்டர்சன், ப. 549.
- ↑ பாட்டர்சன் மற்றும் ஹென்னெச்சி, ப. 714.
- ↑ வாட் ஈஸ் க்ளஸ்டரிங்? வெப்போபீடியா கணினி அகராதி. நவம்பர் 7, 2007 அன்று மீட்டெடுக்கப்பட்டது.
- ↑ பியோவுல்ஃப் டிஃபினிஷன் பரணிடப்பட்டது 2012-10-10 at the வந்தவழி இயந்திரம் பிசி மாகசைன் . நவம்பர் 7, 2007 அன்று மீட்டெடுக்கப்பட்டது.
- ↑ ஆர்கிடெக்சர் ஷார் ஃபார் 06/2007 பரணிடப்பட்டது 2007-11-14 at the வந்தவழி இயந்திரம். சிறந்த 500 சூப்பர் கணிப்பு வலைதளங்கள். அந்தப் பட்டியலில் கணினிகளின் 74.60% க்ளஸ்டர்களைப் பற்றியதாக இருக்கிறது. நவம்பர் 7, 2007 அன்று மீட்டெடுக்கப்பட்டது.
- ↑ ஹென்னெச்சி மற்றும் பாட்டர்சன், ப. 537.
- ↑ எம்பிபி டிஃபினிஷன். பரணிடப்பட்டது 2013-05-11 at the வந்தவழி இயந்திரம் பிசி மாகசைன் . நவம்பர் 7, 2007 அன்று மீட்டெடுக்கப்பட்டது.
- ↑ கிர்க்பாட்ரிக், ஸ்காட் (ஜனவரி 31, 2003). "கம்ப்யூட்டர் சைன்ஸ்: ரஃப் டைம்ஸ் அஹெட்". சைன்ஸ் , தொ. 299. எண். 5607, பக். 668 - 669. DOI: 10.1126/science.1081623
- ↑ 32.0 32.1 32.2 டிஅமோர், மைக்கல் ஆர்., முதன்மை இயக்க அதிகாரி, டீஆர்சி கம்ப்யூட்டர் கார்போரேஷன். "ஸ்டாண்டர்ட் ரீகன்ஃபிகரபிள் கம்ப்யூடிங்". டெலாவேர் பல்கலைக்கழகத்தில் அழைக்கப்பட்ட பேச்சாளர், பிப்ரவரி 28, 2007.
- ↑ போக்கான், ஷாகியா மற்றும் டேனியல் எம். பிரெஸ்ஸெல் (ஆகஸ்ட் 2007). GPUs: ஆன் எமர்ஜிங் பிளாட்ஃபார்ம் ஃபார் ஜெனரல்-பர்பஸ் கம்பூடேஷன் பரணிடப்பட்டது 2016-12-25 at the வந்தவழி இயந்திரம் (பிடீஎஃப்). ARL-SR-154, அமெரிக்க இராணுவ ஆராய்ச்சிக் கூடம். நவம்பர் 7, 2007 அன்று மீட்டெடுக்கப்பட்டது.
- ↑ மாஸ்லென்னிகோவ், ஓலெக் (2002). "சிஸ்டமாடிக் ஜெனரேஷன் ஆஃப் எக்சிகியூடிங் புரோகிராம்ஸ் ஃபார் புரோசெஸ்ஸார் எலிமெண்ட்ஸ் இன் பாரலல் ASIC ஆர் FPGA-பேஸ்ட் சிஸ்டம்ஸ் அண்ட் தேர் டிரான்ஸ்ஃபார்மேஷன் இண்டு VHDL-டிஸ்கிரிப்ஷன்ஸ் ஆஃப் புரோசெஸ்ஸார் எலிமெண்ட் கண்ட்ரோல் யூனிட்ஸ்". பரணிடப்பட்டது 2020-02-11 at the வந்தவழி இயந்திரம் லெக்சர் நோட்ஸ் இன் கம்ப்யூட்டர் சைன்ஸ் , 2328/2002: ப. 272.
- ↑ ஷிமோகாவா, வை.; வை. ஃபுவா மற்றும் என். அராமாகி (18–21 நவம்பர் 1991). எ பாரலல் ASIC VLSI நியூரோகம்ப்யூடர் ஃபார் எ லார்ஜ் நம்பர் ஆஃப் நியூரான்ஸ் அண்ட் பில்லியன் கனெக்ஷன்ஸ் பெர் செகண்ட் ஸ்பீட். IEEE இண்டர்நேஷனல் ஜாயிண்ட் கான்ஃபரன்ஸ் ஆன் நியூரல் நெட்வர்க்ஸ். 3: பக். 2162–67.
- ↑ அக்கென், கெ.பி.; எம்.ஜெ. இர்வின், ஆர்.எம். ஓவென்ஸ் (சூலை 1998). "எ பாரலல் ASIC ஆர்கிடெக்ச்ர் ஃபார் எஃபிஷியண்ட் ஃப்ராக்டல் இமேஜ் கோடிங்". பரணிடப்பட்டது 2012-10-21 at the வந்தவழி இயந்திரம் தி ஜர்னல் ஆஃப் விஎல்எஸ்ஐ சிக்னல் புரோசெசிங் , 19 (2):97–113(17)
- ↑ காஹ்ங், ஆண்ட்ரூ பீ. (சூன் 21, 2004) "ஸ்கோபிங் தி பிராப்ளம் ஆஃப் டிஎஃப்எம் இன் தி செமிகண்டக்டர் இண்டஸ்ட்ரி பரணிடப்பட்டது 2008-01-31 at the வந்தவழி இயந்திரம்." கலிபோர்னியா பல்கலைகழகம், சான் டியாகோ. "தயாரிப்புத் (DFM) தொழில்நுடப்த்திற்கான எதிர்கால திட்டங்கள் வடிவமைப்பு [திரும்பப் பெறமுடியாத செலவு] செலவினங்களைக் குறைத்துக்கொண்டு தயாரிப்புகளில் [திரும்பப் பெறமுடியாத செலவுகள்] - மறைப்புத் தொகுதி மற்றும் விசாரனை அட்டையின் செலவு - நேரடியாக கவனம் செலுத்த வேண்டும், இது இப்போதே 90 nm தொழில்நுட்ப கணுவில் $1 மில்லியனுக்கும் கூடுதலாக இருக்கிறது மேலும் குறைகடத்தி சார்ந்த கண்டுபிடிப்புகளில் பெருமளவு தடையை உருவாக்குகிறது."
- ↑ 38.0 38.1 பாட்டர்சன் மற்றும் ஹென்னெச்சி, ப. 751.
- ↑ சிட்னி ஃபெர்ன்பாச் கிவன் டு எம்பிஐ இன்வண்டர் பில் க்ராப் பரணிடப்பட்டது 2011-07-25 at the வந்தவழி இயந்திரம் என்பது MPI யை "பிரதான HPC தகவல்தொடர்புகளின் இடைமுகம்" என்பதாகக் குறிக்கிறது.
- ↑ ஷென், ஜான் பால் மற்றும் மிக்கோ எச். லிபாஸ்டி (2005). மாடர்ன் புராசெஸ்ஸ்ர் டிசைன்: ஃபண்டமெண்டல்ஸ் ஆஃப் சூப்பர்ஸ்கேலார் புராசெஸ்ஸர்ஸ் . மெக்கிரா-ஹில் புரொஃபெஷனல். ப. 561. ஐஎஸ்பிஎன் 0070570647 "எனினும் அத்தகைய ஆராய்ச்சி - தொடர் நிரல்களின் தானியங்கி இணைப்படுதல் - இன்னமும் சாத்தியப்படவில்லை. படித்தீர்வுகளின் சில குறிப்பிட்ட பிரிவுகளில் தானியங்கி இணைப்படுதல் வெளிப்படுத்தப்பட்டிருந்தாலும், அத்தகைய வெற்றிகள் பெரும்பாலும் கணிக்கக்கூடிய போக்கு கட்டுப்பாடு (எ-டு: நிலையாக உறுதியுடன் இருக்கும் மறுசெய்கை எண்ணிக்கைகளுடன் கூடிய உட்பொதிவுள்ள கண்ணி கட்டமைப்புகள்) மற்றும் நிலையாக மதிப்பீடு செய்யப்படக்கூடிய நினைவக பாங்குடன் (எ-டு: மிதவைப் புள்ளி தரவின் பெரும் பலபரிமாண வரிசைகள் மீது கடந்து செல்லல்) இருக்கும் அறிவியல் மற்றும் எண் பயன்பாடுகளுடன் மட்டும் வரையறுக்கப்பட்டுள்ளது."
- ↑ அசோனோவிக், கிறிஸ்டே மற்றும் பலர். திசம்பர் 18, 2006. தி லாண்ட்ஸ்கேப்ஸ் ஆஃப் பாரலல் கம்ப்யூடிங் ரிசர்ச்: எ வியூ ஃப்ரம் பெர்கெலி (பிடீஎஃப்). கலிபோர்னியா பல்கலைக்கழகம், பெர்கெலி. தொழில்நுட்ப அறிக்கை எண். UCB/EECS-2006-183. பக்கங்கள் 17-19 இல் உள்ள பட்டியலைப் பார்க்கவும்.
- ↑ மெனாபிரியா, எல். எஃப். (1842). ஸ்கெட்ச் ஆஃப் தி அனாலிடிக் என்ஜின் இன்வெண்டெட் பை சார்லஸ் பாப்பேஜ்.. Bibliothèque Universelle de Genève. நவம்பர் 7, 2007 அன்று மீட்டெடுக்கப்பட்டது.
- ↑ 43.0 43.1 43.2 பாட்டர்சன் மற்றும் ஹென்னெச்சி, ப. 753.
- ↑ da Cruz, Frank (2003). "Columbia University Computing History: The IBM 704". Columbia University. பார்க்கப்பட்ட நாள் 2008-01-08.
- ↑ பாரலல் புரோகிராமிங், எஸ். கில், தி கம்ப்யூட்டர் ஜர்னல் தொ. 1 #1, பக்.2-10, பிரித்தானிய கம்ப்யூட்டர் சொசைடி, ஏப்ரல் 1958.
- ↑ 46.0 46.1 46.2 46.3 46.4 Wilson, Gregory V (1994). "The History of the Development of Parallel Computing". Virginia Tech/Norfolk State University, Interactive Learning with a Digital Library in Computer Science. பார்க்கப்பட்ட நாள் 2008-01-08.
- ↑ Anthes, Gry (November 19, 2001). "The Power of Parallelism". Computerworld. Archived from the original on 2008-01-31. பார்க்கப்பட்ட நாள் 2008-01-08.
- ↑ பாட்டர்சன் மற்றும் ஹென்னெச்சி, ப. 749.
- ↑ பாட்டர்சன் மற்றும் ஹென்னெச்சி, பக். 749–50: "பிந்தைய செயல்திட்டங்களில் பயன்படக்கூடிய பல்வேறு தொழில்நுட்பங்களைக் கொண்டுவருவதில் வெற்றிபெற்றபோதிலும், ILLIAC IV ஒரு கணினியாக தோல்வியுற்றது. 1966 ஆம் ஆண்டில் இதற்காக மதிப்பிடப்பட்ட $8 மில்லியன் 1972 ஆம் ஆண்டுக்குள் $31 மில்லியானாக உயர்ந்துவிட்டது, இத்தனைக்கும் திட்டமிட்ட இயந்திரத்தின் கால்பாகமே கட்டப்பட்டிருந்தது. சூப்பர் கணினிகளிலேயே இதுதான் மிகவும் இகழ்தற்குரிய ஒன்றாக இருந்திருக்கக்கூடும். 1965 ஆம் ஆண்டில் தொடங்கப்பட்ட அந்த செயல்திட்டம் தன்னுடைய அசலான முதல் பயன்பாட்டை 1976 ஆம் ஆண்டில் இயக்கியது."
புற இணைப்புகள்[தொகு]
- லாரன்ஸ் லிவர்மோர் தேசிய ஆராய்ச்சிக்கூடம்: இணைக் கணிப்பீடு ஒரு அறிமுகம்பரணிடப்பட்டது 2013-06-10 at the வந்தவழி இயந்திரம்
- டிசைனிங் ஆண்ட் பில்டிங் பாரலல் புரோகிராம்ஸ், ஆசிரியர் ஐயான் ஃபோஸ்டர்
- இண்டர்நெட் பாரலல் கம்ப்யூடிங் ஆர்சிவ் பரணிடப்பட்டது 2002-10-12 at the வந்தவழி இயந்திரம்
- பாரலல் புரோசெசிங் டாபிக் ஏரியா அட் IEEE டிஸ்ட்ரிபியூடெட் கம்ப்யூடிங் ஆன்லைன் பரணிடப்பட்டது 2011-09-28 at the வந்தவழி இயந்திரம்
- பாரலல் கம்ப்யூடிங் வர்க்ஸ் ஃப்ரீ ஆன்லைன் புக் பரணிடப்பட்டது 2011-07-27 at the வந்தவழி இயந்திரம்
- ஃப்ராண்டியர்ஸ் ஆஃப் சூப்பர்கம்ப்யூடிங் ஃப்ரீ ஆன்லைன் புக் கவரிங் டாபிக்ஸ் லைக் அல்கோரிதம்ஸ் அண்ட் இண்டஸ்ட்ரியல் அப்ளிகேஷன்ஸ்
- யூனிவர்சல் பாரலல் கம்ப்யூடிங் ரிசர்ச் சென்டர் பரணிடப்பட்டது 2008-10-20 at the வந்தவழி இயந்திரம்
- கொலம்பியா பல்கலைக்கழகத்தில் இணை நிரலாக்கம் செய்தலுக்கான படிப்பு (ஐபிஎம் டி.ஜெ வாட்சன் X10 செயல்திட்டத்துடன் ஒருங்கிணைந்து) பரணிடப்பட்டது 2010-01-22 at the வந்தவழி இயந்திரம்






