பொன் விகிதம்: திருத்தங்களுக்கு இடையிலான வேறுபாடு

உள்ளடக்கம் நீக்கப்பட்டது உள்ளடக்கம் சேர்க்கப்பட்டது

வரியுள்

12:26, 12 திசம்பர் 2011 இல் நிலவும் திருத்தம்

கணிதவியலிலும் கலையிலும் எவையேனும் இரு அளவுகளின் கூடுதலுக்கும் அவற்றில் பெரிய அளவுக்குமான விகிதமானது, பெரிய அளவுக்கும் சிறிய அளவுக்குமான விகிதத்திற்குச் சமமாக இருந்தால் அந்த இரு அளவுகளும் தங்க விகிதத்தில் (golden ratio) அமைந்துள்ளன எனப்படுகின்றன. இவ்விகிதத்தின் மதிப்பு ஒரு விகிதமுறா மாறிலி எண்ணாகும். இதன் தோராயமான மதிப்பு 1.61803398874989.^[1] தங்க விகிதத்தின் குறியீடு கிரேக்க மொழியின் சிறிய எழுத்து ( $\varphi$ ) (phi) மற்றும் அதன் பெருக்கல் தலைகீழி ${\frac {1}{\varphi }}$ அல்லது $\varphi ^{-1}$ -ன் ,குறியீடு கிரேக்க மொழியின் பெரிய எழுத்து $\Phi$ (Phi) ஆகும்.

{\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi .

விகிதமுறா எண்களின் கணத்தில் இச்சமன்பாட்டிற்கு ஒரு நேர்மத் தீர்வு உள்ளது:

\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\ldots

.

^[1] தங்க விகிதமானது கவின்கலை, ஓவியம், கட்டிடக்கலை, புத்தக வடிவமைப்பு, இயற்கை, இசை, நிதிச்சந்தை...என பல்வகையான துறைகளிலும் பரந்து காணப்படுகிறது.

மறுமலர்ச்சிக் காலத்தில் இருந்தாவது, பல ஓவியர்களும், கட்டிடக் கலைஞர்களும் தமது ஆக்கங்களில் பொன் விகிதத்தைப் பயன்படுத்தினார்கள். இது பொதுவாக பொன் செவ்வக வடிவில் அமைந்தது. நீளமும் அகலமும் பொன் விகிதத்தில் அமைந்த இச் செவ்வகம் அழகியல் அடிப்படையில் மனதுக்கு இதமானது என நம்பப்பட்டது. இவ் விகிதத்தின் தனித்துவமானதும், ஆர்வத்தைத் தூண்ட வல்லதுமான இயல்புகள் காரணமாக கணிதவியலாளர் இதனை ஆராய்ந்தார்கள்.

வரலாறு

பொன் விகிதம், பல்வேறு வகையான ஆர்வங்களைக் கொண்ட அறிஞர்களை 2,400 ஆண்டுகளாக ஈர்த்து வந்துள்ளது.

எக்காலத்தும் சிறந்த சில கணித மூளைகளான பண்டைக் கிரேக்கத்தின் பித்தாகரஸ், இயூக்கிளிட் ஆகியோரில் இருந்து, மத்தியகால இத்தாலியக் கணிதவியலாளராகிய ஃபிபோனாசி, மறுமலர்ச்சிக்கால வானியலாளர் ஜொஹான்னஸ் கெப்லர், ஆகியோரூடாக இன்றைய அறிவியலாளர்களான ஆக்ஸ்போர்ட் இயற்பியலாளர் ரோஜர் பென்ரோஸ் வரையானவர்கள் இந்த எளிமையான விகிதத்தின் இயல்புகள் பற்றி ஆராய்வதற்காகப் பெருமளவு நேரத்தைச் செலவு செய்துள்ளனர். ஆனால், இவ்விகிதத்தின் மீதான ஆர்வம் கணிதவியலாளர்களுக்கு மட்டும் மட்டுப்பட்டதல்ல. உயிரியலாளர்கள், கலைஞர்கள், இசைக்கலைஞர்கள், வரலாற்றாளர்கள், கட்டிடக்கலைஞர்கள், உளவியலாளர்கள் போன்றோரும் இதுபற்றிச் சிந்தித்து இதன் கவர்ச்சியின் அடிப்படைகள் பற்றி விவாதித்துள்ளனர். உண்மையில், கணிதவியலின் வரலாற்றில் வேறெந்த எண்ணையும் விட அதிகமாக எல்லாத் துறைகளையும் சேர்ந்த சிந்தனையாளர்களையும் பொன் விகிதம் ஈர்த்துள்ளது என்று சொன்னால் நியாயமாக இருக்கக்கூடும்.
—மரியோ லிவியோ, பொன் விகிதம்: "பை"யின் வரலாறு, The World's Most Astonishing Number

வடிவவியலில் அடிக்கடி இப் பொன் விகிதம் தோன்றுவதாலேயே பண்டைக் கிரேக்கர்கள் இது பற்றி ஆய்வு செய்தனர். ஒழுங்கான நட்சத்திர ஐங்கோணம், ஒழுங்கான ஐங்கோணம் ஆகியவற்றின் வடிவவியல் தொடர்பில் ஒரு கோட்டை முடிவு மற்றும் இடை விகிதங்களாகப் பிரிக்க வேண்டியது முக்கியமானது. இக் கருத்துருவை பித்தாகரஸ் அல்லது அவரைப் பின்பற்றுவோரே கண்டுபிடித்ததாகக் கிரேக்கர்கள் நம்புகின்றனர். ஒழுங்கான ஐங்கோணத்தை உள்ளடக்கிய ஒழுங்கான நட்சத்திர ஐங்கோணமே பித்தாகோரியர்களின் சின்னமாகும்.

கணக்கிடுதல்

a மற்றும் b -இரண்டும் தங்க விகிதத்தில் அமைந்திருந்தால்:

{\frac {a+b}{a}}={\frac {a}{b}}=\varphi

.

{\frac {a+b}{a}}

-ஐப் பின்வருமாறு சுருக்க:

{\frac {a+b}{a}}=1+{\frac {b}{a}}=1+{\frac {1}{\varphi }}

கிடைக்கிறது.

ஆனால் : ${\frac {a+b}{a}}=\varphi .$

எனவே

1+{\frac {1}{\varphi }}=\varphi .

φ -ஆல் பெருக்க:

\varphi +1=\varphi ^{2}

{\varphi }^{2}-\varphi -1=0

.

இருபடி வாய்ப்பாட்டைப் பயன்படுத்தப் பின்வரும் நேர்மத் தீர்வு கிடைக்கும்:

\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\dots

.

கணிதத்தில்

தங்க விகிதத்தின் இணை

φ -ன் இருபடிச் சமன்பாட்டின் எதிர்மத் தீர்வு (இணையியத் தீர்வு):

-{\frac {1}{\varphi }}=1-\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.61803\,39887\dots

.

இதன் எண் மதிப்பு (≈ 0.618) சிறிய அளவுக்கும் மற்றும் பெரிய அளவுக்குமுள்ள விகிதமாகும் (b/a). சில நேரங்களில் இம்மதிப்பு தங்க விகிதத்தின் இணை என அழைக்கப்படுகிறது.^[2] இதன் குறியீடு Φ:

\Phi ={1 \over \varphi }={1 \over 1.61803\,39887\ldots }=0.61803\,39887\ldots

.

மாறாக Φ பின்வருமாறும் தரப்படலாம்:

\Phi =\varphi -1=1.61803\,39887\ldots -1=0.61803\,39887\ldots .

.

இதிலிருந்து நேர்ம எண்களுக்குள் தங்க விகிதத்தின் பின்வரும் தனித்த பண்பினை அறியலாம்:

{1 \over \varphi }=\varphi -1

.

இதன் தலைகீழி:

{1 \over \Phi }=\Phi +1

.

அதாவது:

0.61803... : 1 = 1 : 1.61803....

மாற்று வடிவங்கள்

φ = 1 + 1/φ -சமன்பாட்டை மீள்வரு முறையில் விரித்து தங்க விகிதத்தினை தொடர் பின்னவடிவில் பெறலாம்:^[3]

\varphi =[1;1,1,1,\dots ]=1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}

தலைகீழி:

\varphi ^{-1}=[0;1,1,1,\dots ]=0+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}

φ² = 1 + φ சமன்பாட்டிலிருந்து தங்க விகிதத்தை தொடர்ச்சியான வர்க்கமூல (முடிவுறா விகிதமுறா மூலம்) வடிவில் பெறலாம்:

\varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\cdots }}}}}}}}

.

தங்க விகிதத்தை முடிலாத் தொடராகப் பெறலாம்:^[4]

\varphi ={\frac {13}{8}}+\sum _{n=0}^{\infty }{\frac {(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}}.

மேலும் பல வடிவங்கள்:

\varphi =1+2\sin(\pi /10)=1+2\sin 18^{\circ }

\varphi ={1 \over 2}\csc(\pi /10)={1 \over 2}\csc 18^{\circ }

\varphi =2\cos(\pi /5)=2\cos 36^{\circ }

\varphi =2\sin(3\pi /10)=2\sin 54^{\circ }.

இவற்றிலிருந்து ஒழுங்கு ஐங்கோணத்தின் மூலைவிட்டத்தின் நீளமானது அதன் பக்கத்தின் நீளத்தைப்போல் φ மடங்கு என்பதையும் ஐந்துமுனையுடைய நட்சத்திர வடிவத்தில் இதுபோன்ற தொடர்புகளையும் அறியலாம்.

வடிவவியல்

ஒரு கோட்டுத்துண்டை தங்க விகிதத்தில் பிரித்தல்

ஒரு கோட்டுத்துண்டை பின்வரும் வடிவியல் வரைமுறையில் தங்க விகிதத்தில் பிரிக்கலாம்:

தரப்பட்ட கோட்டுத்துண்டு AB -க்குச் செங்குத்தாகவும் அதன் நீளத்தில் பாதியாகவும் உள்ள கோட்டுத்துண்டு BC வரைய வேண்டும். செம்பக்கம் AC வரைய வேண்டும்.

C -ஐ மையமாகவும் BC -ஐ ஆரமாகவும் கொண்டு வரையப்படும் வட்டவில் AC-ஐ D புள்ளியில் வெட்டுகிறது.

A -ஐ மையமாகவும் AD -ஐ ஆரமாகவும் கொண்டு வரையப்படும் வட்டவில் AB-ஐ S புள்ளியில் வெட்டுகிறது.

இப்புள்ளி S, கோட்டுத்துண்டு AB -ஐ தங்க விகிதத்தில் பிரிக்கிறது.

தங்க முக்கோணம்

இருசமபக்க முக்கோணம் ABC (கோணங்கள் B, C சமம்), கோணம் C இருசமக்கூறிடப்படும்போது கிடைக்கும் புது முக்கோணம் CXB, மூல முக்கோணம் ABC -க்கு வடிவொத்ததாக அமையும் பண்பினைக் கொண்ட தங்க முக்கோணம்.

கோணம் C = 2α என்க.

இருசமக்கூறிடப்படுவதால்:

கோணம் BCX = α,

கோணம் XCA = α

வடிவொத்த முக்கோணங்களின் பண்பின்படி:

கோணம் CAB = α

முக்கோணம் ABC இருசமபக்க முக்கோணம் என்பதால்:

கோணம் ABC = 2α

மீண்டும் வடிவொத்த முக்கோணங்களின் பண்பின்படி:

கோணம் BXC = 2α

ஒரு முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180° என்பதால், முக்கோணம் ABC -ல்:

5α = 180, α = 36°.

எனவே முக்கோணம் ABC -ன் கோணங்கள் 36°-72°-72°. விரிகோண இருசமபக்க முக்கோணம் AXC (தங்க நோமோன்) -ன் கோணங்கள் 36°-36°-108°.

XB -ன் நீளம் 1, மற்றும் BC -ன் நீளம் φ என்க.

இருசமபக்க முக்கோணங்களின் பண்பின்படி:

XC = XA = φ;

BC = XC = φ;

AC = AB = φ+1.

முக்கோணங்கள் ABC, CXB இரண்டும் வடிவொத்தவை என்பதால்:

AC/BC = BC/BX,

AC = BC²/BX = φ².

ஃ φ² = φ+1, எனவே இங்கு φ தங்க விகிதம். முக்கோணம் ABC தங்க முக்கோணம்.

இதேபோல் பெரிய முக்கோணம் AXC-ன் பரப்பிற்கும் சிறிய முக்கோணம் CXB -ன் பரப்பிற்கும் உள்ள விகிதம் 1/φ (Φ). இதில் முக்கோணங்களின் வரிசையை மாற்றக் கிடைக்கும் விகிதம் φ - 1.

ஐங்கோணம்

ஒரு ஒழுங்கு ஐங்கோணத்தின் ஒரு பக்கத்திற்கும் ஒரு மூலைவிட்டத்திற்குமுள்ள விகிதம் 1/φ. இதன் ஒன்றையொன்று வெட்டிக்கொள்ளும் மூலைவிட்டங்கள் வெட்டிக்கொள்ளும் விகிதம் தங்க விகிதம் ஆகும்.

ஓடோமின் வரைமுறை

${\tfrac {|AB|}{|BC|}}={\tfrac {|AC|}{|AB|}}=\phi$

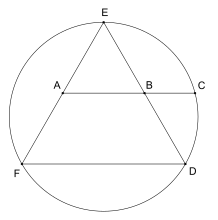
அமெரிக்க கலைஞரும் வடிவவியல் கணித அறிஞருமான ஜார்ஜ் ஓடம் ஒரு சமபக்க முக்கோணத்தைப் பயன்படுத்தி φ -ஐக் காண ஒரு எளிமையான வழியைக் கண்டுபிடித்துள்ளார்:

ஒரு வட்டத்துக்குள் ஒரு சமபக்கமுக்கோணம் வரைய வேண்டும்.
அம்முக்கோணத்தின் இரு பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் கோட்டுத்துண்டை நீட்டித்து அதை வட்டத்தை வெட்டச் செய்ய வேண்டும்.
இரு நடுப்புள்ளிகள் மற்றும் வட்டத்தை வெட்டும் புள்ளி, இம்மூன்றும் தங்க விகிதத்தில் அமையும்.

ஐந்துமுனை நட்சத்திர வடிவம்

ஒரு ஐந்துமுனையுடைய நட்சத்திர வடிவின் வெவ்வேறு நீளங்களுடைய கோட்டுத்துண்டுகளை வேறுபடுத்துவதற்காக வெவ்வேறு நிறங்களில் காட்டப்பட்டுள்ளன. நான்கு நீளங்களும் ஒன்றுக்கொன்று தங்க விகிதத்தில் உள்ளன.

ஐந்துமுனையுடைய நட்சத்திரங்களின் வடிவியலில் தங்க விகிதம் முக்கிய பங்கு வகிக்கிறது. விளிம்புகளின் ஒவ்வொரு வெட்டும் பிற விளிம்புகளை தங்க விகிதத்தில் பிரிக்கிறது. மேலும் சிறிய துண்டின் நீளத்திற்கும் இரு வெட்டும் விளிம்புகளுகளால் அடைபடும் துண்டிற்குமுள்ள விகிதம் φ ஆகும். (நட்சத்திர வடிவின் நடுவிலுள்ள ஐங்கோணத்தின் ஒரு பக்கம்).

இந்த நட்சத்திர வடிவில் 10 இருசமபக்க முக்கோணங்கள் (5 குறுங்கோண இருசமபக்க முக்கோணங்கள், 5 விரிகோண இருசமபக்க முக்கோணங்கள்) உள்ளன. இவை எல்லாவற்றிலும் பெரிய பக்கத்திற்கும் சிறிய பக்கத்திற்குமுள்ள விகிதம் φ. 5 குறுங்கோண இருசமபக்க முக்கோணங்களும் தங்க முக்கோணங்கள். 5 விரிகோண இருசமபக்க முக்கோணங்களும் தங்க நோமோன்கள் (golden gnomons).

டாலமியின் தேற்றம்

ஓர் ஒழுங்கு ஐங்கோணத்தின் தங்க விகிதப் பண்புகளை, அதன் ஒரு உச்சியை நீக்கினால் கிடைக்கும் நாற்கரத்தில் டாலமியின் தேற்றத்தைப் பயன்படுத்திக் காணலாம். நாற்கரத்தின் பெரிய விளிம்பும் மூலைவிட்டங்களும் b, மற்றும் சிறிய விளிம்பு a எனில் டாலமியின் தேற்றத்தின்படி:

b^{2}=a^{2}+ab\,

இச்சமன்பாட்டை $a^{2}$ -ஆல் வகுத்து, மாற்றி அமைக்க:

{b^{2} \over a^{2}}-{b \over a}-1=0\,

இருபடி வாய்ப்பாட்டின்படி நேர்மத் தீர்வு:

{b \over a}={{(1+{\sqrt {5}})} \over 2}

.

மேற்கோள்கள்

↑ ^1.0 ^1.1 The golden ratio can be derived by the quadratic formula, by starting with the first number as 1, then solving for 2nd number x, where the ratios (x + 1)/x = x/1 or (multiplying by x) yields: x + 1 = x², or thus a quadratic equation: x² − x − 1 = 0. Then, by the quadratic formula, for positive x = (−b + √(b² − 4ac))/(2a) with a = 1, b = −1, c = −1, the solution for x is: (−(−1) + √((−1)² − 4·1·(−1)))/(2·1) or (1 + √(5))/2.
↑ Weisstein, Eric W., "Golden Ratio Conjugate", MathWorld.
↑ Max. Hailperin, Barbara K. Kaiser, and Karl W. Knight (1998). Concrete Abstractions: An Introduction to Computer Science Using Scheme. Brooks/Cole Pub. Co. பன்னாட்டுத் தரப்புத்தக எண்:0-534-95211-9. http://books.google.com/?id=yYyVRueWlZ8C&pg=PA63&dq=continued-fraction+substitute+golden-ratio.
↑ Brian Roselle, "Golden Mean Series"

வெளி இணைப்புகள்

"Golden Section" by Michael Schreiber, Wolfram Demonstrations Project, 2007.
"The Myth That Will Not Go Away" Mathematical Association of America 2007
Weisstein, Eric W., "Golden Ratio", MathWorld.
"Researcher explains mystery of golden ratio". PhysOrg. December 21, 2009..
Knott, Ron. "The Golden section ratio: Phi". Information and activities by a mathematics professor.
The Pentagram & The Golden Ratio. Green, Thomas M. Updated June 2005. Archived November 2007. Geometry instruction with problems to solve.

[th:อัตราส่วนทอง]]

[quadform-1] 1.0 ^1.1 The golden ratio can be derived by the quadratic formula, by starting with the first number as 1, then solving for 2nd number x, where the ratios (x + 1)/x = x/1 or (multiplying by x) yields: x + 1 = x², or thus a quadratic equation: x² − x − 1 = 0. Then, by the quadratic formula, for positive x = (−b + √(b² − 4ac))/(2a) with a = 1, b = −1, c = −1, the solution for x is: (−(−1) + √((−1)² − 4·1·(−1)))/(2·1) or (1 + √(5))/2.

[MathWorld_GR_Conjugate-2] Weisstein, Eric W., "Golden Ratio Conjugate", MathWorld.

[3] Max. Hailperin, Barbara K. Kaiser, and Karl W. Knight (1998). Concrete Abstractions: An Introduction to Computer Science Using Scheme. Brooks/Cole Pub. Co. பன்னாட்டுத் தரப்புத்தக எண்:0-534-95211-9. http://books.google.com/?id=yYyVRueWlZ8C&pg=PA63&dq=continued-fraction+substitute+golden-ratio.

[4] Brian Roselle, "Golden Mean Series"

[1]

[2]

[3]

[4]