முழு எண்

கணிதத்தில் முழு எண்கள் அல்லது நிறை எண்கள் (இலத்தீன்: integer அதாவது முழுமை) எனப்படுவன நேர்ம இயற்கை எண்களையும் (1, 2, 3, …), அவற்றின் எதிர்மங்களையும் (−1, −2, −3, ...) மற்றும் சுழி இலக்கத்தையும் குறிப்பனவாகும். முழு எண்களைப் பின்னப் பகுதியற்ற எண்கள் எனவும் கொள்ளலாம். எடுத்துக்காட்டாக 13, 9, மற்றும் −1204 ஆகியவை முழு எண்கள்; 1.25, 5½, ஆகியவை முழு எண்கள் அல்ல.
முழுஎண்களின் கணம் "Z" அல்லது என்ற குறியீடுகளால் குறிக்கப்படுகிறது[1][2]. விகிதமுறு எண்களின் கணத்திற்கும் மெய்யெண்களின் கணத்திற்கும் முழுஎண்களின் கணம் உட்கணமாக அமைகிறது. மேலும் இக் கணம், எண்ணுறு முடிவிலி கணமாகும்.
முழுவெண்களின் கணம் மிகச்சிறிய குலமாகவும் மிகச்சிறிய வளையமாகவும் இருக்கும். இயற்கணித எண் கோட்பாட்டில், இயற்கணித முழுவெண்களிலில் இருந்து வேறுபடுத்திக் காட்டப்படுவதற்காக, முழுவெண்கள் "விகிதமுறு முழுவெண்கள்" என அழைக்கப்படுகின்றன. விகிதமுறு எண்களாக இருக்கக்கூடிய இயற்கணித முழுவெண்களாக, இந்த விகிதமுறு முழுவெண்கள் உள்ளன.
குறியீடு[தொகு]
Z என்ற குறியீடு வெவ்வேறு கணங்களைக் குறிப்பதற்குப் பல்வேறான அறிஞர்களால் பயன்படுத்தப்படுகிறது:
- நேர்ம முழுவெண்களுக்கு: Z+, Z+ or Z>
- எதிர்மமில்லா முழுவெண்களுக்கு Z≥
- பூச்சியமில்லா முழுவெண்களுக்கு Z≠
- சிலர் பூச்சியமில்லா முழுவெண்களுக்கு Z* என்பதையும், வேறு சிலர் இக்குறியீட்டை எதிர்மமில்லா முழுவெண்களுக்கு அல்லது {–1, 1} கணத்திற்குப் பயன்படுத்துகின்றனர்.
வரைபடத்தில்[தொகு]

முடிவிலா நீளமுள்ள ஒரு எண்கோட்டின்மீது சம இடைவெளியில் அமையும் தனித்த புள்ளிகளாக முழுஎண்களைக் குறிக்கலாம். முழுஎண் கோட்டில், எதிரிலா முழுஎண்கள் சுழிக்கு வலப்புறமும், எதிர் முழுஎண்கள் சுழிக்கு இடப்புறத்திலும் குறிக்கப்படுகின்றன.
இயற்கணிதப் பண்புகள்[தொகு]
அடைவுப் பண்பு[தொகு]
இயல் எண்களின் கணத்தைப் போன்றே, முழுஎண்களின் கணமும் (Z) கூட்டல் மற்றும் பெருக்கல் ஆகிய இரு ஈருறுப்புச் செயலிகளைப் பொறுத்து அடைவு பெற்றது ஆகும். அதாவது இரு முழுஎண்களின் கூடுதல் மற்றும் பெருக்கற்பலன் இரண்டும் முழுஎண்களாகவே இருக்கும். 0 மற்றும் எதிர் இயல் எண்கள் உள்ளதால் Z இல் உள்ளதால் இக் கணம் கழித்தலைப் பொறுத்தும் அடைவு பெற்றுள்ளது.
ஆனால் இரு முழுஎண்களை ஒன்றை மற்றொன்றால் வகுக்கும்போது கிடைக்கும் எண் முழுஎண்ணாக இருக்கவேண்டியதில்லை என்பதால் வகுத்தலைப் பொறுத்து முழுஎண்கள் கணம் அடைவு பெறவில்லை. இதேபோல, அடுக்கேற்றத்தைப் பொறுத்தும் முழுஎண்கள் கணம் அடைவுபெறவில்லை.
கூட்டல், பெருக்கலைப் பொறுத்த பண்புகளின் அட்டவணை[தொகு]
a, b மற்றும் c ஆகிய மூன்று முழுஎண்களுக்குக் கூட்டல் மற்றும் பெருக்கல் செயல்களைப் பொறுத்த அடிப்படைப் பண்புகள் கீழுள்ள அட்டவணையில் தரப்பட்டுள்ளன:
| கூட்டல் | பெருக்கல் | |
|---|---|---|
| அடைவுப் பண்பு | a + b ஒரு முழுஎண் | a × b ஒரு முழுஎண் |
| சேர்ப்புப் பண்பு | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| பரிமாற்றுப் பண்பு | a + b = b + a | a × b = b × a |
| முற்றொருமை உறுப்பு இருத்தல் | a + 0 = a | a × 1 = a |
| நேர்மாறு உறுப்பு இருத்தல் | a + (−a) = 0 | நேர்மாறு உறுப்பு கிடையாது |
| பங்கீட்டுப் பண்பு | a × (b + c) = (a × b) + (a × c) and (a + b) × c = (a × c) + (b × c) | |
| சுழி பகுப்பான் | a × b = 0 எனில் a = 0 அல்லது b = 0 (அல்லது இரண்டும்) | |
கூட்டலைப் பொறுத்து[தொகு]
ஏபெல் குலம்[தொகு]
மேலே தரப்பட்டுள்ள அட்டவணயின் படி ஈருறுப்புச் செயலியான கூட்டலைப் பொறுத்து, Z ஆனது அடைவுப் பண்பு, சேர்ப்புப் பண்பு, முற்றொருமை உறுப்பு இருத்தல், நேர்மாறு உறுப்பு இருத்தல், பரிமாற்றுப் பண்பு ஆகிய ஐந்து பண்புகளையும் நிறைவு செய்கிறது. எனவே (Z, +) ஒரு ஏபெல் குலமாகிறது.
சுழற் குலம்[தொகு]
சுழியற்ற ஒவ்வொரு முழுஎண்ணையும் 1 + 1 + ⋯ + 1 அல்லது (−1) + (−1) + ⋯ + (−1) என்ற முடிவுறுக் கூட்டல் வடிவில் எழுதமுடியும் என்பதால் (Z, +) ஒரு சுழற் குலமாகவும் உள்ளது. உண்மையில் முடிவிலி சுழற்குலமாக அமைவது (Z, +) மட்டுமே. ஏனென்றால் வேறு ஏதாவது முடிவிலி சுழற்குலங்கள் இருந்தாலும், அவை (Z, +) உடன் குலச் சமஅமைவியம் கொண்டவையாய் அமையும்.
பெருக்கலைப் பொறுத்து[தொகு]
குலம்[தொகு]
- குலமாவதற்குத் தேவையான நான்கு பண்புகளில் முதல் மூன்று பண்புகளைக் கொண்டிருந்தாலும், நான்காவது பண்பான பெருக்கலுக்கான பொறுத்த நேர்மாறு உறுப்புகள் இல்லாமையால் (Z, x) குலம் ஆகாது.
- பெருக்கலைப் பொறுத்து அடைவுப் பண்பு, சேர்ப்புப் பண்பு, முற்றொருமை உறுப்பு இருத்தல் ஆகிய மூன்று பண்புகளையும் நிறைவு செய்வதால், (Z, x) ஒரு ஒற்றைக்குலம் ஆகிறது. மேலும் இம் மூன்று பண்புகளுடன் பெருக்கலைப் பொறுத்த பரிமாற்றுப் பண்பும் நிறைவு செய்யப்படுவதால் (Z, x) ஒரு பரிமாற்று ஒற்றைக்குலம் ஆகும்.
வளையம், களம்[தொகு]
- (Z, +) ஏபெல் குலமாகவும், (Z, x) ஒற்றைக்குலமாகவும் மேலும் கூட்டல் மற்றும் பெருக்கலைப் பொறுத்த பங்கீட்டுப் பண்பும் (, )
நிறைவு பெறுவதால் முழுஎண்களின் கணம் (Z, +, x) ஒரு பரிமாற்று வளையம் ஆகும்.
- வளையமாக இருந்தபோதும் பெருக்கலைப் பொறுத்த நேர்மாறு உறுப்புகள் இல்லாமையால் முழுஎண்களின் கணம் ஒரு களமாக முடியாது.
முழு வரிசைப் பண்பு[தொகு]
முழுஎண்கள் கணம், மேல்வரம்பும் கீழ்வரம்புமற்ற முழு வரிசையுடைய கணமாகும். Z இன் வரிசைப்படுத்தப்பட்ட வடிவம்: :… −3 < −2 < −1 < 0 < 1 < 2 < 3 < … சுழியைவிடப் பெரிய முழுஎண்கள் நேர் முழுஎண்கள் எனவும், சுழியைவிடச் சிறிய முழுஎண்கள் எதிர் முழுஎண்கள் எனவும் அழைக்கப்படும். சுழி நேர் முழு எண்ணோ அல்லது எதிர் முழுஎண்ணோ கிடையாது.
முழுஎண்கள் முழு வரிசைப் பண்புடையாதாக இருப்பதால் பின்வரும் முடிவுகள் சாத்தியமாகின்றன:
- a < b , c < d எனில் a + c < b + d
- a < b , 0 < c எனில், ac < bc.
எண்ணளவை[தொகு]
முழு எண்கள் கணத்தின் எண்ணளவை அல்லது முதலெண் ℵ0 (Aleph number) ஆகும். இதனை முழுவெண்கள் கணத்திலிருந்து (Z) இயலெண்கள் கணத்திற்கு (N) ஒரு இருவழிக்கோப்பு (அதாவது உள்ளிடுகோப்பு மற்றும் முழுக்கோப்பு) அமைத்து விளக்கலாம்:
- N = {0, 1, 2, …}:
{… (−4,8) (−3,6) (−2,4) (−1,2) (0,0) (1,1) (2,3) (3,5) …}
- N = {1, 2, 3, ...}:
- {… (−4,8) (−3,6) (−2,4) (−1,2) (0,1) (1,3) (2,5) (3,7) …}
சார்பின் ஆட்களத்தை முழுவெண்களாக ((Z) மட்டுப்படுத்தினால், Z இல் உள்ள ஒவ்வொரு எண்ணுக்கும் ஒத்ததாக N இல் ஒரேயொரு எண் மட்டுமே இருக்கும். மேலும் எண்ணளவையின் வரையரைப்படி, Z மற்றும் N இரண்டின் எண்ணளவைகளும் சமம் என்பதை அறியலாம். அதாவது முழுவெண்கள் கணத்தின் எண்ணளவை இயலெண்களின் கணத்தின் எண்ணளவைக்குச் சமமாகும்.
அமைப்பு[தொகு]
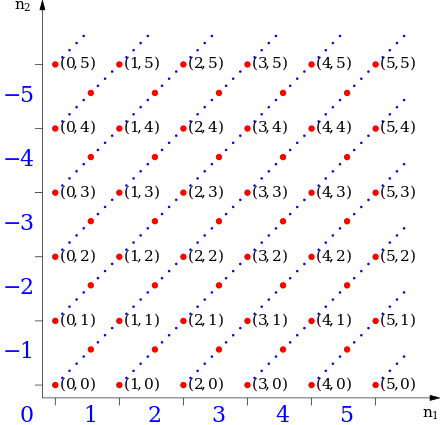
துவக்கப் பள்ளிகளில் முழுவெண்கள் என்பவை இயலெண்கள், பூச்சியம், இயலெண்களின் எதிர்ம எண்கள் ஆகியவை சேர்ந்ததாகக் கொள்ளப்படுகிறது. எனினும் இவ்விதமான வரையறை முறைகளால் ஒவ்வொருவிதமான வரையறைக்கும் அடிப்படை எண்கணிதச் செயல்களை வெவ்வேறுவிதமாக வரையறுக்க வேண்டிய நிலை ஏற்படும். மேலும் இந்த செயல்கள் எண்கணித விதிகளை நிறைவு செய்யும் என்பதை நிறுவுதலும் கடினமானதாக இருக்கும்.[3] எனவே பெரும்பாலும் தற்கால கணக்கோட்பாட்டுக் கணிதத்தில், வேறுபாடின்றி எண்கணிதச் செயல்களை வரையறுக்கக் கூடியதாக முழுவெண்களின் அமைப்பு பயன்படுத்தப்படுகிறது.[4][5] இம்முறையில் முழுவெண்கள் இயல் எண்களின் வரிசைச் சோடிகளின் சமானப் பகுதிகளாக அமைக்கப்படுகிறது ((a,b)).[6]
a இலிருந்து b ஐக் கழிக்கக் கிடைக்கும் விடையாக (a,b) என்பது புரிந்துகொள்ளப்படுகிறது.[6] 1 − 2, 4 − 5 இரண்டும் ஒரே எண்ணைக் குறிக்கும் என்பதைக் காட்ட இந்த வரிசைச் சோடிகளின் மீதான சமான உறவு, ~ கீழுள்ள விதிகளை நிறைவுசெய்யும் வகையில் வரையறுக்கப்படுகிறது:
- என இருந்தால்,
முழுவெண்களின் கூட்டல் மற்றும் பெருக்கல் செயல்களை இயலெண்களின் மீதான அச்செயல்களைக் கொண்டு வரையறுக்கலாம்;[6] (a,b) ஐ உறுப்பாகக் கொண்ட சமானப் பகுதியை [(a,b)] எனக் குறித்தால்:
வரிசைச் சோடியின் வரிசையை மாற்றுவதன் மூலம் ஒரு முழுவெண்ணின் எதிரெண்ணைப் பெறலாம்:
இதன்மூலம் கழித்தலை கூட்டல் நேர்மாற்றின் கூட்டலாக வரையறுக்கலாம்:
முழுவெண்களின் வரிசையின் வரையறை:
- என இருந்தால், இருந்தால் மட்டுமே,
- ஆகும்.
இந்த எண்கணிதச் செயல்களின் வரையறையானது, சமானப் பகுதிகளின் உருவகிப்புகளின் தேர்வைப் பொறுத்து மாறாதது என்பதை எளிதாகச் சரிபார்க்க முடியும்.
மேற்கோள்கள்[தொகு]
- ↑ Miller, Jeff (2010-08-29). "Earliest Uses of Symbols of Number Theory". பார்க்கப்பட்ட நாள் 2010-09-20.
- ↑ Peter Jephson Cameron (1998). Introduction to Algebra. Oxford University Press. பக். 4. பன்னாட்டுத் தரப்புத்தக எண்:978-0-19-850195-4. http://books.google.com/books?id=syYYl-NVM5IC&pg=PA4.
- ↑ Mendelson, Elliott (2008), Number Systems and the Foundations of Analysis, Dover Books on Mathematics, Courier Dover Publications, p. 86, ISBN 9780486457925.
- ↑ Ivorra Castillo: Álgebra
- ↑ Frobisher, Len (1999), Learning to Teach Number: A Handbook for Students and Teachers in the Primary School, The Stanley Thornes Teaching Primary Maths Series, Nelson Thornes, p. 126, ISBN 9780748735150.
- ↑ 6.0 6.1 6.2 Campbell, Howard E. (1970). The structure of arithmetic. Appleton-Century-Crofts. பக். 83. பன்னாட்டுத் தரப்புத்தக எண்:0-390-16895-5. https://archive.org/details/structureofarith00camp.









![{\displaystyle [(a,b)]+[(c,d)]:=[(a+c,b+d)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ada63de55374aa09013be65caa1c33aa0164ecb3)
![{\displaystyle [(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ea8c51ad5f2968fcf5788eb220d4f4463b28588)
![{\displaystyle -[(a,b)]:=[(b,a)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/951d0171ed1edf705e70392352f3d07b94ed4c74)
![{\displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef8af489c7cff40fe4cfe66d5a706837fc0a6df6)

![{\displaystyle [(a,b)]<[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5f5d9d3f2ef39e8cf90692589f0b97945454536)