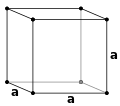
படிக அமைப்பு

இன்சுலின் படிகம்.

கனிமவியல் மற்றும் படிகவுருவியலில், படிக அமைப்பு என்பது ஓர் படிகத்தில் அணுக்கள் குறிப்பிட்ட அமைப்பில் உள்ளதைக் குறிப்பதாகும்.படிகம் (crystal) என்பது அதனை உருவாக்கும் அணுக்கள், மூலக்கூறுகள், அயன்கள் என்பன ஒழுங்கமைவான முறையில், திரும்பத் திரும்ப வரும் வடிவொழுங்கில் ஓர் அணிக்கோவை அமைந்துள்ள ஒரு திண்மமாகும். அவ்வணிக்கோவையின் முனைகள் கொண்டு ஓர் பெட்டி அமைக்கப்படுமானால் அது ஓர் அலகுஅறையாக எடுத்துக் கொள்ளப்படுகிறது.இந்த அலகுஅறைகள் அணிக்கோவையை நிரப்புகின்றன. இந்த அலகுஅறையின் நீள,அகலங்கள் மற்றும் கோணங்கள் அணிக்கோவையின் வரையளவுகளாக குறிக்கப்படுகின்றன.படிகத்தின் சமச்சீர் பண்புகள் மூன்று அச்சுகளிலும் அமைகிறது. படிகத்தின் கட்டமைப்பும் சமச்சீர்மையும் பிளவு, இலத்திரன் பிணையமைப்பு மற்றும் ஒளி குறித்த பண்புகள் என அதன் பண்புகளை வரையறுக்கின்றன.

அலகுக் கூடு

படிகங்களில் அணுக்கள் அல்லது அயனிகள் ஒழுங்கான முப்பரிமான அமைப்பில் அமைந்துள்ளன. படிகத் திடப்பொருள் அல்லது படிகத்தில் உள்ள மிகச்சிறிய மீண்டும் மீண்டும் தோன்றக் கூடிய முப்பரிமாண வடிவமைப்பு அலகுக் கூடு எனப்படும். அலகுக் கூடு என்பது படிகத் திடப் பொருளின் எளிமையான அடிப்படைப் பகுதியாகும். அலகுக் கூட்டினை அறிவதன் மூலம் படிகத்தின் அமைப்பை அறியலாம்.

ஏழு அணிக்கோவை அமைப்பு

அணிக்கோவைகளின் அச்சு அமைப்பினைக்கொண்டு படிக அமைப்புகள் ஏழு குழுக்களாக பிரிக்கப்படுகின்றன. ஒவ்வொரு அணிக்கோவையும் மூன்று அச்சுகளிலும் ஓர் குறிப்பிட்ட அமைப்பைக் கொண்டிருக்கும்.

ஏழு அணிக்கோவை அமைப்புகள் (குறைந்ததிலிருந்து கூடுதல் சமச்சீர்மை கொண்டது வரை)	14 ப்ராவை அணிக்கோவைகள்				எடுத்துக்காட்டுகள்
1. முச்சாய்வு (triclinic)(none)
2. ஒருசாய்வு (monoclinic) (1 diad)	simple	base-centered
3. சமமில்லா முச்செங்குத்து <orthorhombic) (3 perpendicular diads)	simple	base-centered	body-centered	face-centered
4. சமபக்க முச்சாய்வகம் (rhombohedral) (1 triad)
5. சதுரப்பட்டகம் (tetragonal) (1 tetrad)	simple	body-centered
6. அறுகோணப்பட்டகம் (hexogonal) (1 hexad)
7. கனசதுரம் (4 triads)	simple (SC)	body-centered (BCC)	face-centered (FCC)

வெளியிணைப்புகள்

• Appendix A from the manual for Atoms, software for XAFS
• Intro to Minerals: Crystal Class and System
• Introduction to Crystallography and Mineral Crystal Systems
• Crystal planes and Miller indices
• Interactive 3D Crystal models
• Crystal Lattice Structures: Other Crystal Structure Web Sites