திணிவு மையம்: திருத்தங்களுக்கு இடையிலான வேறுபாடு
No edit summary |
|||
| வரிசை 135: | வரிசை 135: | ||
\frac13(y_a+y_b+y_c)\right).</math> |
\frac13(y_a+y_b+y_c)\right).</math> |
||
எனவே |
எனவே ஈர்ப்புமைய அச்சுதூரங்களின் வாயிலாக முக்கோணத்தின் திணிவு மையம்: |
||
:<math>\left(\frac13,\frac13,\frac13\right)</math> |
:<math>\left(\frac13,\frac13,\frac13\right)</math> |
||
முக்கோணம் ஒரு சீரான தாள் அல்லது தகட்டால் செய்யப்பட்டிருந்தால் (அல்லது அதன் நிறை மூன்று உச்சிகளிலும் சீராக பிரிக்கப்பட்டிருந்தால்) நடுக்கோட்டுச்சந்தியானது முக்கோணத்தின் |
முக்கோணம் ஒரு சீரான தாள் அல்லது தகட்டால் செய்யப்பட்டிருந்தால் (அல்லது அதன் நிறை மூன்று உச்சிகளிலும் சீராக பிரிக்கப்பட்டிருந்தால்) நடுக்கோட்டுச்சந்தியானது முக்கோணத்தின் நிறை மையமாகவும் அமையும். மாறாக முக்கோணத்தின் நிறையானது சீரான அடர்த்தியுடன் அதன் [[சுற்றளவு|சுற்றளவில்]] பரவியிருந்தால், நிறை மையமானது திணிவு மையத்துடன் பொருந்தாது. |
||
முக்கோணத்தின் பரப்பானது, அதன் ஏதேனும் ஒரு பக்கத்தின் நீளத்தின் மடங்காக அமையும் அப்பக்கத்திலிருந்து திணிவு மையத்தின் செங்குத்து தூரத்தின் 1.5 |
முக்கோணத்தின் பரப்பானது, அதன் ஏதேனும் ஒரு பக்கத்தின் நீளத்தின் மடங்காக அமையும் அப்பக்கத்திலிருந்து திணிவு மையத்தின் செங்குத்து தூரத்தின் 1.5 மடங்காகவும் முக்கோணத்தின் பரப்பு அமையும்.<ref>Johnson, Roger A., ''Advanced Euclidean Geometry'', Dover, 2007 (orig. 1929): p. 173, corollary to #272.</ref> |
||
முக்கோணத்தின் பரப்பு: |
முக்கோணத்தின் பரப்பு: |
||
| வரிசை 152: | வரிசை 152: | ||
பன்முகியின் உச்சிகள்: <math>{v_0,\ldots,v_n}</math>, உச்சிகளை வெக்டர்களாக கருதினால்: |
பன்முகியின் உச்சிகள்: <math>{v_0,\ldots,v_n}</math>, உச்சிகளை வெக்டர்களாக கருதினால்: |
||
பன்முகியின் திணிவு மையம்: |
|||
:<math>C = \frac{1}{n+1}\sum_{i=0}^n v_i.</math> |
:<math>C = \frac{1}{n+1}\sum_{i=0}^n v_i.</math> |
||
பன்முகியின் நிறையானது, பன்முகி முழுவதும் சீராக பரவியிருந்தாலோ அல்லது உச்சிகளில் சமமாகப் பிரிக்கப்பட்டிருந்தாலோ திணிவு மையமானது |
பன்முகியின் நிறையானது, பன்முகி முழுவதும் சீராக பரவியிருந்தாலோ அல்லது உச்சிகளில் சமமாகப் பிரிக்கப்பட்டிருந்தாலோ திணிவு மையமானது, நிறை மையத்துடன் பொருந்தும். |
||
=== பல்கோணத்தின் திணிவு மையம் === |
=== பல்கோணத்தின் திணிவு மையம் === |
||
19:23, 10 செப்டெம்பர் 2011 இல் நிலவும் திருத்தம்

வடிவவியலில் ஒரு தளவுருவத்தின் அல்லது இருபரிமாண வடிவம் X -ன் திணிவு மையம்(centroid), வடிவுசார் மையம்(geometric center) அல்லது ஈர்ப்பு மையம்(barycenter) என்பது, அவ்வடிவத்தை சம விலக்களவு(moment) கொண்ட இரு பகுதிகளாகப் பிரிக்கும் கோடுகள் அனைத்தும் வெட்டிக்கொள்ளும் புள்ளியாகும். சாதாரணமாக, திணிவு மையத்தை X -லுள்ள அனைத்துப் புள்ளிகளின் சராசரியாகக் கருதலாம். திணிவு மையத்தின் இந்த இருபரிமாண வரையறையை n -பரிமாணத்திற்கும் நீட்டிக்கலாம். n -பரிமாணத்திலுள்ள ஒரு பொருள் X -ன் திணிவுமையம் என்பது, அதனை சம விலக்களவு கொண்ட இரு பாகங்களாகப் பிரிக்கும் மீத்தளங்கள் (hyperplane) வெட்டிக்கொள்ளும் புள்ளியாகும்
இயற்பியலில், திணிவு மையம் என்பது ஒரு பொருளினுடைய வடிவத்தின் வடிவுசார் மையத்தைக் குறிக்கிறது. ஆனால் ஈர்ப்பு மையம் என்பது, அது பயன்படுத்தப்படும் இடத்தைப் பொறுத்து, வடிவுசார் மையத்தை மட்டுமல்லாது நிறை மையம்(center of mass) அல்லது புவியீர்ப்பு மையத்தையும்(center of gravity) குறிக்கலாம். சாதாரணமாக, ஒரு பொருளின் நிறை மையம் (மற்றும் சீரான ஈர்ப்பு மண்டலத்தின் புவியீர்ப்பு மையம்) என்பது, அப்பொருளிலுள்ள அனைத்துப் புள்ளிகளின், அண்மை அடர்த்தி அல்லது தன்எடைகளால் எடையிடப்பட்ட சராசரியாகும். ஒரு பொருளின் அடர்த்தி சீரானதாக இருக்குமானால் அப்பொருளின் நிறை மையமும் அப்பொருளின் வடிவத்தின் திணிவு மையமும் ஒன்றாக இருக்கும்.
புவியியலில் பூமியின் மேற்பரப்பு மண்டலம் ஒன்று, அம்மேற்பரப்பின் மீதே ஆரைப்போக்கில் வீழ்த்தப்பட்ட நிலையில் அதன் திணிவு மையமானது, அம்மேற்பரப்பின் புவியியல் மையம் என அழைக்கப்படுகிறது.
பண்புகள்
ஒரு குவிவான பொருளின் திணிவு மையமானது எப்பொழுதும் அப்பொருளுக்குள்ளேயே அமையும். குவிவாக இல்லாத பொருளின் திணிவு மையம் அப்பொருளுக்கு வெளியில் அமையலாம். எடுத்துக்காட்டாக, ஒரு வளையம் அல்லது கிண்ணத்தின் திணிவு மையங்கள் அவற்றின் மைய வெற்றுப்பகுதியில் அமைகின்றன.
ஒரு பொருளின் திணிவு மையம் வரையறுக்கப்பட்டிருந்தால், அது அப்பொருளின் சமஅளவை உருமாற்றங்களின் சமச்சீர் குலத்தின் நிலைப்புள்ளியாகும். குறிப்பாக, ஒரு பொருளின் வடிவுசார் மையமானது அதன் அனைத்து சமச்சீர் மீத்தளங்களின் வெட்டுப்பகுதியில் அமையும். ஒழுங்குப் பலகோணம், ஒழுங்கு பண்முகத்திண்மம், உருளை, செவ்வகம், சாய்சதுரம், வட்டம், கோளம், நீள்வட்டம், நீள்வட்டத்திண்மம் போன்ற பல வடிவங்களின் திணிவு மையங்களை இம்முறையில்தான் காண முடியும்.
- ஒரு இணைகரத்தின் திணிவு மையமானது, அதன் மூலைவிட்டங்கள் வெட்டும் புள்ளியாகும். ஆனால் நாற்கரங்களுக்கு இது பொருந்தாது.
இதேபோல் இடப்பெயர்ச்சி உருமாற்றத்திற்கு நிலைப்புள்ளிகள் எதுவும் இடையாது என்பதால், சமச்சீர் இடப்பெயர்ச்சி உருமாற்றமுடைய பொருட்களுக்கு, ஒன்று திணிவு மையம் கிடையாது, அப்படியே இருந்தாலும் அது அப்பொருளுக்கு வெளியே அமையும்.
திணிவு மையம் காணல்
குண்டு நூல் முறை
கீழே காட்டப்பட்டுள்ள ஒரு சீரான இருபரிமாணத் தகட்டின்(படம்-a) திணிவு மையத்தை ஒரு குண்டு நூல் மற்றும் ஊசியைக் கொண்டு பரிசோதனை மூலம் காணலாம்.
- (படம்-b)தகட்டின் ஒரு முனையை, அது எளிதாக சுழலக்கூடியவகையில் ஊசியில் மாட்டிவிட வேண்டும். பிறகு குண்டு நூலை ஊசியிலிருந்து தொங்கவிட வேண்டும். இப்போது அக்குண்டு நூலின் நிலையை அத்தகட்டில் குறித்துக் கொள்ள வேண்டும். இதேபோல் மீண்டும் தகட்டை வேறொரு முனையில் மாட்டிவிட்டு, குண்டுநூலின் நிலையைக் குறிக்க வேண்டும். இப்பொழுது தகட்டில் குண்டு நூலின் இரு வேறுபட்ட நிலைகளைக் குறிக்கும் கோடுகள் இருக்கும்.
- (படம்-c)அவ்விரு கோடுகளும் சந்திக்கும் புள்ளி அத்தகட்டின் திணிவு மையமாகும்.
இந்த சோதனை மூலம் சீரான அடர்த்தியும் மாறாத வடிவமும் உடைய எந்தவொரு இரு பரிமாணப் பொருளுக்கும் திணிவு மையம் காணலாம்.
 |
 |
 |
| (a) | (b) | (c) |
இம்முறையைக் குவிவல்லாத வடிவங்களுக்கும் சீரான அடர்த்தியுடைய திடப்பொருள்களுக்கும் நீட்டிக்கலாம்(கோட்பாட்டில்). ஆனால் குண்டு நூல்களின் நிலைகளைக் குறிப்பதற்கு வரைதலைத் தவிர்த்து மாற்று முறைகளைப் பயன்படுத்த வேண்டும்.
முடிவுறு எண்ணிக்கையுள்ள புள்ளிகளுக்கு
முடிவுறு எண்ணிக்கை கொண்ட புள்ளிகள்: : in
இப்புள்ளிகளின் திணிவு மையம்:
வடிவத்தைப் பிரிப்பது மூலம்
ஒரு தளவுருவை, எளிய வடிவங்களாக முடிவுறு என்ணிக்கையில் பிரித்து அதன் திணிவு மையத்தைக் காணலாம்.
தளவுரு:
- பிரிக்கப்பட்ட எளிய வடிவங்கள்:
- ,
இவை ஒவ்வொன்றின் பரப்பு .
- இப்பரப்புகளின் திணிவு மையங்கள்:
- -ன் திணிவு மையம்:
பிரிக்கப்பட்ட பகுதிகளில் ஒன்றின்மீது ஒன்றாகப் படியும் -லுள்ள துளைகளையும் -க்கு வெளியில் அமையும் பகுதிகளையும் குறைக்குறியுடைய பரப்புகளைக் கொண்டு சரி செய்யலாம். ஒரு குறிப்பிட்ட புள்ளி -யைக் கொண்டுள்ள எல்லாப் பகுதிகளின் பரப்புகள் -ன் குறிகளின் கூடுதல், அப்புள்ளி -ல் இருந்தால் 1 ஆகவும் இல்லையெனில் 0 ஆகவும் இருக்குமாறு -க்களின் குறிகளை எடுத்துக்கொள்ள வேண்டும்.
எடுத்துக்காட்டு:
படம் (a) -லுள்ள வடிவம்:
- மிகைக்குறி கொண்ட பரப்புடைய சதுரம் மற்றும் முக்கோணமாகவும், குறைக்குறி கொண்ட பரப்புடைய வட்டத்துளையாகவும் படம் (b) ல் பிரித்துக் காட்டப்பட்டுள்ளது.
 |
 |
 |
| (a) | (b) | (c) |
- பிரிக்கப்பட்ட பகுதிகளின் திணிவு மையத்தை, எளிய வடிவங்களின் திணிவு மையப் பட்டியலில் இருந்து கண்டுபிடிக்கலாம். எடுத்துக்கொண்ட வடிவத்தின் திணிவு மையம் மூன்று புள்ளிகளின் எடையிடப்பட்ட சராசரியாகும். வடிவத்தின் இடது விளிம்பிலிருந்து திணிவு மையத்தின் கிடைமட்ட நிலை:
இதே வாய்ப்பாடு எந்தவொரு முப்பரிமாணப் பொருளுக்கும் பொருந்தும். ஆனால் ஒவ்வொரு -ம் பரப்பாக இல்லாமல், -ன் கன அளவாக இருக்க வேண்டும். எந்தவொரு பரிமாணம் -லும் -ன் எந்தவொரு உட்கணத்திற்கும் இந்த வாய்ப்பாடு பொருந்தும். பிரிக்கப்பட்ட பகுதிகளின் பரப்பிற்குப் பதில் -பரிமாண அளவுகளை எடுக்க வேண்டும்
தொகையிடல் மூலம்
-ன் உட்கணம் X -ன் திணிவு மையத்தைத் தொகையிடல் மூலம் காணலாம்:
இத்தொகையீடானது, வெளிமீது முழுவதுமாக தொகையிடப்படுகிறது. g என்பது X உட்கணத்தின் சிறப்பியல்புச் சார்பாகும். எனவே g -ன் மதிப்பு X -க்குள் 1. மற்றும் X -க்கு வெளியே 0 ஆகும். வாய்ப்பாட்டிலுள்ள பின்னத்தின் பகுதியானது, உட்கணம் X -ன் அளவையாகும்(measure). (X -ன் அளவை பூச்சியமாக இருந்தாலோ அல்லது தொகையீடு விரிந்தாலோ இவ்வாய்ப்பாட்டைப் பயன்படுத்த முடியாது.)
திணிவு மையத்தின் மற்றொரு வாய்ப்பாடு:
இங்கு,
- Ck என்பது C -ன் k-அச்சுதூரம்.
- Sk(z) என்பது, xk = z என்ற சமன்பாடு வரையறுக்கும் மீத்தளமும் X -ம் வெட்டும் பகுதியின் அளவையாகும். இதிலும் வாய்ப்பாட்டின் பின்னத்தின் பகுதியானது, X -ன் அளவையாகும்
ஒரு தளவுருவத்தின் பொருள்-நிறை மையத்தின் அச்சுதூரங்கள்:
இங்கு,
- வடிவம் X -ன் பரப்பு A ;
- Sy(x) என்பது x அச்சுதூரத்தில் அமையும் நிலைக்கோட்டுடன் X -ன் வெட்டுப்பகுதியின் நீளமாகும்.
- Sx(y) என்பது Sy(x) -ல் அச்சுகளை மாற்றிக் கணக்கிடும் ஒத்த மதிப்பாகும்.
L-வடிவப் பொருளின் திணிவு மையம்
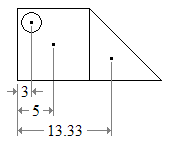
- இது, படம்-1 லுள்ள L- வடிவப் பொருளின் திணிவு மையம் காணும் முறையாகும்:
- படம் 2 -ல் உள்ளபடி, L-வடிவத்தை , இரு செவ்வகங்களாகப் பிரிக்க வேண்டும். இந்த இரு செவ்வகங்களின் மூலைவிட்டங்களை வரைய வேண்டும். ஒவ்வொரு செவ்வகத்திலும் அதன் மூலைவிட்டங்கள் வெட்டும் புள்ளி அதன் திணிவு மையமாகும். இந்த திணிவு மையங்களை இணைத்துக் கோடு AB வரைதல் வேண்டும். தரப்பட்ட L-வடிவப் பொருளின் திணிவு மையம் இக்கோட்டின் மேல் அமையும்.
- படம் 3 -ல் உள்ளபடி, L-வடிவத்தை இரு செவ்வகங்களாகப் பிரிக்க வேண்டும். இவ்விரு செவ்வகங்களின் மூலைவிட்டங்களை வரைந்து அவற்றின் திணிவு மையங்களைக் காண வேண்டும். இந்த இரு திணிவு மையங்களை இணத்து கோடு CD வரைதல் வேண்டும். L-வடிவப் பொருளின் திணிவு மையம் இக்கோட்டின் மேல் அமைய வேண்டும்.
- L-வடிவப் பொருளின் திணிவு மையம் கோடுகள் AB மற்றும் CD மேல் அமையும் என்பதால் இவ்விரு கோடுகளும் வெட்டும் புள்ளியான O, திணிவு மையமாகும். இப்புள்ளி, L-வடிவப் பொருளுக்குள் அமைவது சாத்தியமில்லை.
முக்கோணம் மற்றும் நான்முகத் திண்மம்
|
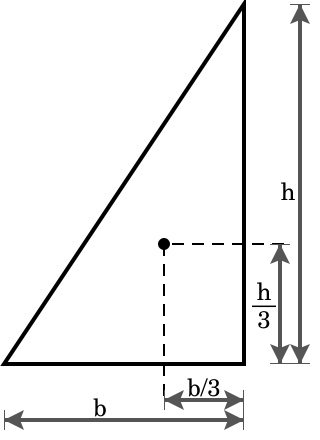
ஒரு முக்கோணத்தின் திணிவு மையமானது அம்முக்கோணத்தின் நடுக்கோடுகள் வெட்டிக்கொள்ளும் புள்ளியாகும். முக்கோணத்தின் திணிவு மையமானது நடுக்கோட்டுச்சந்தி எனவும் அழைக்கப்படுகிறது. திணிவு மையமானது ஒரு நடுக்கோட்டை 2:1 என்ற விகிதத்தில் முக்கோணத்தின் உச்சியிலிருந்து பிரிக்கிறது. திணிவு மையம், முக்கோணத்தின் ஒரு பக்கத்திற்கும் அதன் எதிர் உச்சிக்கும் இடையேயுள்ள செங்குத்து தூரத்தில் ⅓ அளவிலான இடத்தில் அமைகிறது (படத்தைப் பார்க்கவும்). திணிவு மையத்தின் கார்டீசியன் அச்சுதூரங்கள் முக்கோணத்தின் மூன்று உச்சிகளின் அச்சுதூரங்களின் சராசரியாகும்.
முக்கோணத்தின் மூன்று உச்சிகளின் அச்சுதூரங்கள்:
- , , மற்றும் எனில்:
திணிவு மையத்தின் அச்சுதூரங்கள்:
எனவே ஈர்ப்புமைய அச்சுதூரங்களின் வாயிலாக முக்கோணத்தின் திணிவு மையம்:
முக்கோணம் ஒரு சீரான தாள் அல்லது தகட்டால் செய்யப்பட்டிருந்தால் (அல்லது அதன் நிறை மூன்று உச்சிகளிலும் சீராக பிரிக்கப்பட்டிருந்தால்) நடுக்கோட்டுச்சந்தியானது முக்கோணத்தின் நிறை மையமாகவும் அமையும். மாறாக முக்கோணத்தின் நிறையானது சீரான அடர்த்தியுடன் அதன் சுற்றளவில் பரவியிருந்தால், நிறை மையமானது திணிவு மையத்துடன் பொருந்தாது.
முக்கோணத்தின் பரப்பானது, அதன் ஏதேனும் ஒரு பக்கத்தின் நீளத்தின் மடங்காக அமையும் அப்பக்கத்திலிருந்து திணிவு மையத்தின் செங்குத்து தூரத்தின் 1.5 மடங்காகவும் முக்கோணத்தின் பரப்பு அமையும்.[1]
முக்கோணத்தின் பரப்பு:
1/2 bh = (3/2) x ( b) x (h/3) =1.5 (b) x (h/3)
நான்முகத்திண்மத்தின் திணிவு மையமானது அதன் ஒவ்வொரு உச்சியையும் அவ்வுச்சிக்கு எதிர் முக்கோணப் பக்கத்தின் திணிவு மையத்தை இணைக்கும் கோடுகள் வெட்டிக்கொள்ளும் புள்ளியாகும். இக்கோடுகள், திணிவு மையத்தினால் உச்சியிலிருந்து 3:1 என்ற விகிதத்தில் பிரிக்கப்படுகின்றன.
இதனை n-பரிமாண பன்முகிக்குப்(simplex) பொதுமைப்படுத்தலாம்.
பன்முகியின் உச்சிகள்: , உச்சிகளை வெக்டர்களாக கருதினால்:
பன்முகியின் திணிவு மையம்:
பன்முகியின் நிறையானது, பன்முகி முழுவதும் சீராக பரவியிருந்தாலோ அல்லது உச்சிகளில் சமமாகப் பிரிக்கப்பட்டிருந்தாலோ திணிவு மையமானது, நிறை மையத்துடன் பொருந்தும்.
பல்கோணத்தின் திணிவு மையம்
தனக்குள்ளாக வெட்டிக்கொள்ளாத மூடிய பல்கோணத்தின் திணிவு மையம்:
பல்கோணத்தின் n உச்சிகள்: (x0,y0), (x1,y1), ..., (xn−1,yn−1)
- திணிவு மையம்: (Cx, Cy),[2]
இங்கு A என்பது பல்கோணத்தின் குறியிடப்பட்ட பரப்பாகும்.
இந்த வாய்ப்பாடுகளில் பலகோணத்தின் உச்சிகள் சுற்றளவு வழியாக வரிசையாக எடுத்துக்கொள்ளப்படுகிறது. உச்சிகள் ( xn , yn ) மற்றும் ( x0 , y0 ) இரண்டும் ஒன்றாகக் கருதப்படுகின்றன. உச்சிகள் கடிகார திசையில் எடுத்துக்கொள்ளப்பட்டால் மேற்கண்டவாறு கணக்கிடப்படும் பரப்பு A, குறைக்குறி கொண்டதாக அமையும். எனினும் திணிவு மையத்தின் அச்சுதூரங்கள் இதனால் மாறுவதில்லை.
கூம்பு மற்றும் பிரமிடின் திணிவு மையங்கள்
கூம்பு மற்றும் பிரமிடின் திணிவு மையமானது, முகட்டிலிருந்து அடிப்பக்கத்தின் திணிவு மையத்தை இணைக்கும் கோட்டின் மீது அமைகிறது. திடக்கூம்பு மற்றும் திடப்பிரமிடின் திணிவு மையம் அடிப்பக்கத்திலிருந்து முகட்டின் தூரத்தில் ¼ அளவிலான இடத்தில் அமைகிறது. அடிப்பக்கம் இல்லாத(உள்ளீடற்ற) கூம்பு மற்றும் பிரமிடின் திணிவு மையம் அடித்தளத்திலிருந்து முகட்டின் தூரத்தில் 1/3 அளவில் அமையும்.
மேற்கோள்கள்
- ↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover, 2007 (orig. 1929): p. 173, corollary to #272.
- ↑ Calculating the area and centroid of a polygon
வெளி இணைப்புகள்
- Encyclopedia of Triangle Centers by Clark Kimberling. The centroid is indexed as X(2).
- Characteristic Property of Centroid at cut-the-knot
- Barycentric Coordinates at cut-the-knot
- Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge