பாம்ப்பெயூவின் தேற்றம்
பாம்ப்பெயூவின் தேற்றம் (Pompeiu's theorem) என்பது உருமேனியக் கணிதவியலாளர் திமிட்டிரி பாம்ப்பெயூவால் (Dimitrie Pompeiu) கண்டுபிடிக்கப்பட்ட ஒரு யூக்ளீட் வடிவியல் கூற்றாகும். இது ஒரு எளிய தேற்றம்.
தேற்றத்தின் கூற்று:
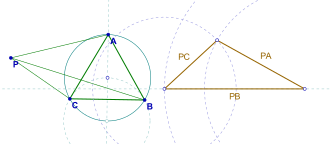
- ABC ஒரு சமபக்க முக்கோணம். இந்த முக்கோணத்தின் தளத்தில் அமைந்த ஒரு புள்ளி P எனில் PA, PB, PC ஆகிய மூன்றும் ஒரு முக்கோணத்தை அமைக்கும்.[1][2]

இத்தேற்றத்தை எளிதாக நிறுவலாம்:
B ஐப் பொறுத்து 60° சுழற்ற, A உச்சியானது C ஆகவும் P ஆனது P ' ஆகவும் இடம் மாறுகிறது என்க. இப்பொழுது,
இவ்விரண்டு முடிவுகளிலிருந்தும் முக்கோணம் PBP ' ஒரு சமபக்க முக்கோணம் என அறியலாம். மேலும்
- ஆக இருக்கும்.
எனவே,
- .
அதாவது PCP ' முக்கோணத்தின் பக்கங்கள் ஒவ்வொன்றும் PA, PB, PC ஆகியவற்றுக்குச் சமமாக இருக்கின்றன. எனவே PA, PB, PC மூன்றும் சேர்ந்து ஒரு முக்கோணத்தை அமைக்கும்.[1][2]
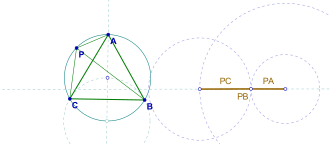
மேலும் புள்ளி P ஆனது முக்கோணத்தின் சுற்று வட்டத்தின் மீது இருந்தால், PA, PB, PC மூன்றும் ஒரு சிதைந்த முக்கோணத்தை அமைக்கும். மூன்று நீளங்களின் பெரியதாகவுள்ளது மற்ற இரு நீளங்களின் கூட்டுத்தொகைக்குச் சமமாக இருக்கும். இக்கூற்று வான் இசுக்கூட்டனின் தேற்றம் ஆகும்.[1]
இத்தேற்றத்தை பாம்ப்பெயூ 1936 இல் வெளியிட்டார். எனினும் செருமானியக் கணிதவியலாளரான மோபியசு 1852 ஆம் ஆண்டிலேயே இதைவிட பொதுமையான தேற்றமாக யூக்ளிடிய தளத்திலுள்ள நான்கு புள்ளிகளுக்கானத் தேற்றத்தை வெளியிட்டிருந்தார். அவர் பாம்ப்பெயூவின் தேற்றத்தின் கூற்றினை தனது தேற்றத்தின் ஒரு சிறப்புவகையாக அளித்திருந்தார். இக்காரணத்தால் இத்தேற்றமானது "மோபியசு-பாம்ப்பெயூ தேற்றம்" எனவும் அறியப்படுகிறது..[3]
மேற்கோள்கள்[தொகு]
- ↑ 1.0 1.1 1.2 Jozsef Sandor: On the Geometry of Equilateral Triangles. Forum Geometricorum, Volume 5 (2005), pp. 107–117
- ↑ 2.0 2.1 Titu Andreescu, Razvan Gelca: Mathematical Olympiad Challenges. Springer, 2008, பன்னாட்டுத் தரப்புத்தக எண் 9780817646110, pp. 4-5
- ↑ D. MITRINOVIĆ, J. PEČARIĆ, J., V. VOLENEC: History, Variations and Generalizations of the Möbius-Neuberg theorem and the Möbius-Ponpeiu. Bulletin Mathématique De La Société Des Sciences Mathématiques De La République Socialiste De Roumanie, 31 (79), no. 1, 1987, pp. 25–38 (JSTOR)
வெளியிணைப்புகள்[தொகு]
- MathWorld's page on Pompeiu's Theorem
- Pompeiu's theorem at cut-the-knot.org




