கணித மாறிலி
கணித நிலையெண் (ஆங்கிலம்: Mathematical constant) அல்லது கணித மாறிலி என்பது ஒரு சில வகையில் இன்றியமையாத பண்புகள் கொண்ட ஒரு சிறப்பு எண் ஆகும். இது பெரும்பாலும் மெய்யெண்ணாகும். அவ்வாறு இன்றியமையாத கணிதப் பண்புகள் இல்லாத சில எண்களும் வரலாற்றுக் காரணங்களால் நிலையெண்களாக விளங்குகின்றன. நிலையெண்கள் பல காலங்களாகப் படித்தும், பலமுறை பதின்ம எண்களாகக் கணிக்கப்பட்டும் உள்ளது.
பெரும்பாலான கணித நிலையெண்கள், விவரிக்கக்கூடிய மெய் எண்களாகவும், கணிக்கக்கூடிய மெய் எண்களாகவும் (சைத்தினின் நிலையெண் விதிவிலக்கு) விளங்குகின்றன.
உதாரணம்:
இங்கு a,b,c என்பன நிலையெண். x மாறெண்: அதாவது x வெவ்வேறு பெறுமானங்கள் எடுக்கலாம், ஆனால் a,b,c என்பன நிலையான பெறுமானம் கொண்டவை. இந்த உதாரணத்தில் நிலையெண்கள் பல்லுறுப்பியின் குணகங்களாக அமைகின்றன. இவற்றில் c ஆனது x0 இன் குணகமாகும்.
கணிதத்தின் நிலையெண்களில் மிகச் சிறப்பானவை மூன்று. அவற்றின் குறியீடுகள் உலகனைத்திலும் எல்லா மொழிகளிலும் ஒரே விதமாக இருப்பதே அவற்றின் முக்கியத்துவத்தைக் காட்டுகின்றன. அவை
• அடுக்குமாறிலி e (the exponential)
• π என்ற கிரேக்க எழுத்தால் அறியப்படும் பை, மற்றும்,
• கற்பனை எண் என்று தவறுதலாகவே குறிக்கப்பட்டு வழக்கில் அப்படியே நிலைபெற்றிருக்கும் i.
பொதுவான கணித நிலையெண்கள்[தொகு]
கணித ஒப்புருக்களுடன் இணைந்துள்ள e, π மற்றும் பைகென்பௌம் நிலையெண்கள் போன்றவை புறநிலைக் கோட்பாடுகளையும், யூக்கிலிடியன் வடிவவியல் பகுப்பாய்வு மற்றும் ஏரண வரைவுகள் போன்றவற்றையும் விளக்கப் பயன்படுகிறது. ஏப்பெரேஸ் நிலையெண்கள் மற்றும் கோல்டன் விகிதம் போன்ற கணித நிலையெண்கள் எதிர்பாரா வண்ணம் கணிதத்தை விட்டு வெளியே பயன்படுகின்றன.
ஆர்சிமிடீஸ் நிலையெண் π[தொகு]

π = 3.14159….
இதை 1767 இல் லாம்பர்ட் ஒரு விகிதமுறா எண் என்று நிறுவினார். 1882 இல் லிண்டெமன் இதுவும் ஒரு விஞ்சிய எண்ணே என்று நிறுவி சாதனை புரிந்தார்.
யூக்கிலிடியன் வடிவவியலில், π நிலையெண்ணின் இயற்கையான விளக்கத்தை "ஓர் விட்டம் கொண்ட ஒரு வட்டத்தின் சுற்றளவே π" எனக் காட்டினாலும், சில வேறு கணிதப் பாடங்களிலும் இது பயன்படுகிறது. எடுத்துக்காட்டாக, சிக்கல் பகுப்பாய்வில் காசியன் தொகையீடு, எண் கோட்பாட்டில் ஒன்றின் வேர்கள் மற்றும் நிகழ்த்தகவில் காசி விரிவரிசை. எப்படியாயினும், இதன் வட்டம் தூய கணிதத்தினுள் மட்டுமே காணப்படுவதில்லை. மாறாக, கெய்சென்பெருக்கின் அறுதியின்மைக் கொள்கை போன்று இயற்பியலில் பல்வேறு வாய்ப்பாடுகளிலும் காணப்படுகிறது. அண்டவியல் நிலையெண் போன்ற நிலையெண்களும் இந்த π நிலையெண்ணைப் பயன்படுத்துகின்றன. இயற்பியலில் காணப்படும் இந்த π நிலையெண், விதிகளிலும், வாய்ப்பாடுகளிலும் மிக எளிதாக விளக்கக்கூடியதாக திகழ்கின்றது. எடுத்துக்காட்டாக, இரண்டு மின்னூட்டுகளின் இடையில் காணப்படும் மின்னிலை விசையின் பருமையும், அதற்கிடையில் உள்ள தொலைவிடமும் கீழ் சதுரமாக்கப்படுவது கூலும் விதியெனப்படும். இதனைப் பின்வருமாறு பை நிலையெண்ணைப் பயன்படுத்தி எழுதலாம்.
வெற்றிடத்தின் மின்காப்பு நிலையெண்ணான -க்கு இடையில் இவ்வாய்ப்பட்டின் கீழுள்ள என்னும் காரணி ஒரு ஆரம் கொண்ட உருண்டையின் மேற்பரப்பினைக் குறிக்கிறது. இதனால் இது தெளிவுறக் காணப்படுகிறது.
ஆய்லர் எண் e[தொகு]
- மேலும் பார்க்க: அடுக்குமாறிலி e ஒரு விகிதமுறா எண்
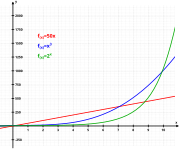
e = 2.718281828459... இது ஒரு விகிதமுறா எண் (irrational number) மட்டுமல்ல; ஒரு விஞ்சிய எண்ணுங்கூட (transcendental number) . இது விகிதமுறா எண் என்பதை ஆய்லர் 1737 இல் நிறுவினார். விஞ்சிய எண் என்பதை 1873 இல் ஹெர்மைட் என்பவர் நிலைநாட்டினார். இதை ஆய்லர் எண் என்று சொல்வது பொருந்தாது என்ற மாற்றுக்கருத்தும் உண்டு.
ஆய்லர் எண் அல்லது அடுக்க வளர்ச்சி நிலையெண் (மாறிலி) பெரும்பாலான கணிதப் பாடங்களிலில் காணப்படுகின்றன. அதில் ஒரு கூடிய பொருள்விளக்கம் பின்வரும் வாய்ப்பாட்டின் மதிப்பாகும்.
பைகென்பௌம் நிலையெண்கள் α மற்றும் δ[தொகு]
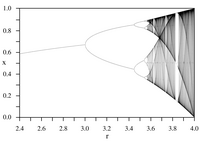
தொடர் மீள்செய்கை குறிப்பிடல் என்பது இயக்கக் கட்டகங்களுக்கு எளிதாக திகழ்கிறது. இது போன்ற மீள்செய்கை செயல்முறையினால் காணப்படும் நிலையெண்கள் இரண்டிற்கும், மிட்செல் பைகென்பௌம் (Mitchell Feigenbaum) என்ற இயற்பியலாளரின் நினைவாக பைகென்பௌம் நிலையெண்கள் என பெயரிடப்பட்டன. அவை இருகூறாக்க வரைப்படமும், இருமடி மீப்புள்ளியும் கொண்ட தகவுப்பொருத்தக் குறிப்புப்படங்களின் கணித வேறுபாடற்றவைகள் ஆகும்.
தகவுப்பொருத்த வரைபடம் என்பது ஒரு எளிய நேரியலற்ற இயக்க கட்டகத்தில் காணப்படும் ஒழுங்கின்மை நிலை எப்படி என்பதற்கு மேற்கோள் காட்டப்படும் பல்லுறுப்பு வரைபடமாகும். இராபருட்டு மே என்னும் அசுதிரேலிய உயிரியலாளரின் 1976-இன் ஆய்வுத்தாளில் இந்த வரைபடும் முதலில் பிரபலமானது. பியர் பிரான்சுவா வேர்கோல்சிட்டு முதலில் உருவாக்கிய தகவுப்பொருத்த சமன்பாட்டிற்கு இணையான தனித்த கால மாதிரி ஓவிய ஒப்புருவாக ஆய்வுத்தாளில் இந்த வரைபடம் வெளியானது ஆகும். இதன் வேறுபாட்டு சமன்பாடு மறுபிறப்பு மற்றும் தேய்தல் ஆகிய இரண்டு விளைவுகளையும் அறிவதற்கு பயன்படுத்தப்படுகிறது.
அப்பெறீயின் நிலையெண் ζ(3)[தொகு]
இரீமன் ஜீட்டா சார்பின் சிறப்பு மதிப்பாக இது விழங்கினாலும், அப்பெறீய் நிலையெண் இயற்கையாக பல்வேறு புறநிலை சிக்கல்களில் காணப்படுகின்றன. துளிம மின்னியக்கவியலைப் பயன்படுத்தி கணிக்கப்பட்ட மின்னணுவின் சுழல்காந்த விகிதத்தின் இரண்டாம் மற்றும் மூன்றாம் நிலை மதிப்பிலும் இது காணப்படுகிறது. ζ(3)-இன் தோராயமான எண்மதிப்பு 1.2020569031595942853997381615114499907649862923404988 என்பதாகும். இதை கணித மென்பொருளான வுஃப்ரேம் நிருவனத்தின் தளத்தில் இணைப்பினால் இயங்கிப்பார்க்கலாம் [1].
அமைகண எண் i[தொகு]
இதை கற்பனை எண் என்றும் சொல்வதுண்டு. ஆனால் இது அப்படியொன்றும் கற்பனையில் மாத்திரம் இருக்கும் எண்ணல்ல. சிக்கல் தளத்தில் (complex plane) ஒவ்வொரு புள்ளிக்கும் இரண்டு ஆயங்கள் உள்ளன. அவைகளில் (0, 1) என்ற புள்ளி தான் அமைகண எண் i . எந்த பலக்கெண்ணையும் i ஆல் பெருக்கினால் பலக்கெண்தளத்தில் அவ்வெண்ணின் இடம் 90 பாகை அல்லது சுழியளவு இடச்சுழியாகத் திரும்பும். அதனால் இதையே மறுபடியும் i ஆல் பெருக்கினால் (0,1) என்ற இடத்தில் இருக்கும் i (-1,0) என்ற இடத்திற்குப் போய்ச் சேரும். இதைத்தான் கீழேயுள்ள சமன்பாடு சொல்கிறது:
ஆய்லருடைய முற்றொருமைச்சமன்பாடு[தொகு]
eiπ = -1
இதுதான் ஆய்லருடைய முற்றொருமைச் சமன்பாடு. இதனில் மூன்று சிறப்பு மாறிலிகளும் சம்பந்தப்படுகின்றன என்பது இதன் முதல் சிறப்பு. இதைத்தவிர இந்த முற்றொருமைக்கு இன்னும் பல சிறப்புகளும் உள்ளன.








