வளைவு (கணிதம்)
கணிதத்தில் வளைவு (curvature) என்பது பொதுவாக ஒரு வடிவவியல் வடிவமானது தட்டையாக இல்லாமல் எவ்வளவு வேறுபட்டுள்ளது என்பதைக் காட்டுகிறது. ஒரு வட்டத்தின் வளைவு வட்டத்தின் மீதுள்ள அனைத்துப் புள்ளிகளிலும் சமமாக இருக்கும். மேலும் அதன் மதிப்பு வட்டத்தின் ஆரத்தின் தலைகீழியாகும். சிறிய (ஆரம்) வட்டங்கள் மிக வளைந்து, அதிகமான வளைவு உடையவையும் பெரிய வட்டங்கள் சிறிதே வளைந்து சிறியளவு அளவு கொண்டவையாகவும் இருக்கும். தளத்தில் (இரு பரிமாணம்) வளைவு ஒரு திசையிலி. ஆனால் முப்பரிமாணத்தில் வளைவு ஒரு திசையானாகும்.
தளத்தில் அமையும் வளைவரைகளின் வளைவு[தொகு]
கணிதவியலாளர் கோஷி, (Cauchy) ஒரு வளைவரையின் வளைவு மையத்தை (C) அவ்வளைவரையின் நுண்ணளவில் நெருக்கமான (infinitely close) செங்கோடுகள் சந்திக்கும் புள்ளி எனவும், ஒரு புள்ளியில் வளைவு ஆரத்தை அப்புள்ளிக்கும் வளைவு மையத்திற்கும் இடைப்பட்ட தூரம் எனவும், வளைவு மதிப்பை ஆரத்தின் தலைகீழி எனவும் வரையறுக்கிறார்.[1]
C என்பது ஒரு தளத்தில் அமைந்த ஒரு வளைவரை எனில், அதன் மீதுள்ள ஒரு புள்ளியானது தனது அண்மையில் நகரும்போது அப்புள்ளியில் வரையப்படும் தொடுகோட்டின் மாறுபாட்டின் அளவைத் தருவது வளைவாகும். இதன் விளக்கம் வெவ்வேறு விதங்களில் அணுகப்படுகிறது.
வடிவவியல் நோக்கில்:
- ஒரு நேர்கோட்டின் வளைவு பூச்சியம் என்பது தெளிவு.
- R அலகு ஆரமுள்ள ஒரு வட்டத்திற்கு, R இன் மதிப்பு அதிகமானால் வளைவு குறைவாகவும் R இன் மதிப்பு குறைவானால் வளைவு அதிகமாகவும் இருக்கும். அதாவது வட்டத்தின் வளைவு அதன் ஆரத்தின் தலைகீழியாக வரையறுக்கப்படுகிறது.
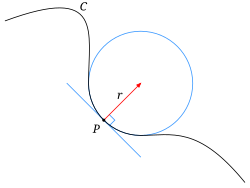
- தரப்பட்ட ஒரு வளைவரை C இன் மீதுள்ள ஒரு புள்ளி P எனில்:
அப்புள்ளியின் அண்மையில் தோராயமாக அவ்வளைவரையை ஒத்து அமையும் ஒரு வட்டமானது (கோடு), அந்த வளைவரைக்கு அப்புள்ளியில் அமையும் ஒட்டு வட்டம் (osculating circle) எனப்படும்.
P புள்ளியில் வளைவரையின் வளைவு என்பது இந்த ஒட்டு வட்டத்தின் (கோட்டின்) வளைவாகும். அதாவது ஒட்டு வட்டத்தின் ஆரத்தின் தலைகீழி.
இயற்பியல் நோக்கில்:
- வளைவினை இயற்பியல் மூலமாகவும் விளக்கலாம்.
ஒரு துகள் சீரான வேகத்தில் ஒரு வளைவரையின் (C) மீது நகர்கிறது எனில்:
நேரம் s -ஐ வளைவரையின் பண்பளவையாகக் கொண்டால், அலகு தொடுகோட்டுத் திசையன் T ஆனதும் நேரத்தைப் பொறுத்ததாக அமையும். வளைவு இந்த தொடுகோட்டுத் திசையனின் மாறுவீதத்தின் எண்ணளவையாக அமையும்.
குறியீட்டில்:

இது அந்தத் துகளின் முடுக்கத்தின் அளவாகவும், முடுக்கத் திசையனாகவும் அமையும்.
வளைவரையின் அலகுத் தொடுகோட்டுத் திசையன் எவ்வளவு வேகமாக சுழல்கிறது என்பதை வளைவு தருகிறது. வளைவரை அதிகத் திசை மாற்றமில்லாது கிட்டத்தட்ட ஒரே திசையில் இருக்குமானால் அலகுத் தொடுகோட்டுத் திசையன் சிறிதளவே மாறும். இதனால் வளைவின் மதிப்பும் மிகச் சிறிதாக இருக்கும். ஆனால் வளைவரை அதிகமான திருப்பம் கொண்டிருந்தால் அலகுத் தொடுகோட்டுத் திசையனின் மாற்றமும் அதிகமாக இருக்கும். அதனால் வளைவின் மதிப்பும் அதிகமாகும்.
குறிப்புகள்[தொகு]
- ↑ *Borovik, Alexandre; Katz, Mikhail G. (2011), "Who gave you the Cauchy--Weierstrass tale? The dual history of rigorous calculus", Foundations of Science, arXiv:1108.2885, எண்ணிம ஆவணச் சுட்டி:10.1007/s10699-011-9235-x
{{citation}}: Italic or bold markup not allowed in:|journal=(help)
மேற்கோள்கள்[தொகு]
- Coolidge, J.L. "The Unsatisfactory Story of Curvature". The American Mathematical Monthly, Vol. 59, No. 6 (Jun. - Jul., 1952), pp. 375–379
- Sokolov, D.D. (2001), "Curvature", in Hazewinkel, Michiel (ed.), Encyclopedia of Mathematics, Springer, பன்னாட்டுத் தரப்புத்தக எண் 978-1556080104
- Morris Kline: Calculus: An Intuitive and Physical Approach. Dover 1998, பன்னாட்டுத் தரப்புத்தக எண் 978-0-486-40453-0, p. 457-461 (restricted online copy, p. 457, கூகுள் புத்தகங்களில்)
- A. Albert Klaf: Calculus Refresher. Dover 1956, பன்னாட்டுத் தரப்புத்தக எண் 978-0-486-20370-6, p. 151-168 (restricted online copy, p. 151, கூகுள் புத்தகங்களில்)
- James Casey: Exploring Curvature. Vieweg+Teubner Verlag 1996, பன்னாட்டுத் தரப்புத்தக எண் 978-3-528-06475-4
வெளி இணைப்புகள்[தொகு]
Graphical illustrations of the curvature of curves
என்பதில் ஊடகங்கள் உள்ளன.
- Create your own animated illustrations of moving Frenet-Serret frames and curvature (Maple-Worksheet)
- The History of Curvature பரணிடப்பட்டது 2007-11-06 at the வந்தவழி இயந்திரம்
- Curvature, Intrinsic and Extrinsic at MathPages






