ரோலின் தேற்றம்
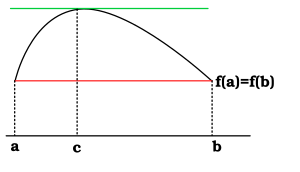
வகை நுண்கணிதத்தில், ரோலின் தேற்றத்தின் (Rolle's theorem) படி, ஒரு வகையிடத்தக்கச் சார்புக்கு, இரு வெவ்வேறு புள்ளிகளில் சமமான மதிப்புகள் இருந்தால், அவ்விரு புள்ளிகளுக்கு இடையே ஏதாவது ஒரு புள்ளியில் அச்சார்பின் முதல் வகைக்கெழு பூச்சியமாக இருக்கும், அதாவது அவ்விரு புள்ளிகளுக்கிடையே சார்பின் வளைவரையின்மீது ஒரு புள்ளியில் (நிலைப் புள்ளி) தொடுகோட்டின் சாய்வு பூச்சியமாகும்.
தேற்றத்தின் திட்ட வடிவம்[தொகு]
- - ஒரு மெய்மதிப்புச் சார்பு. இச்சார்பு,
- மூடிய இடைவெளி [a, b]-ல் தொடர்ச்சியானதாகவும்,
- திறந்த இடைவெளி (a, b)-ல் வகையிடத்தக்கதாகவும்,
- எனவும் இருந்தால்,
- என்றவாறு ஏதாவது ஒரு மதிப்பு, இருக்கும்.
இடைமதிப்புத் தேற்றத்தின் நிறுவலுக்கு,ரோலின் தேற்றம் பயன்படுகிறது. இடைமதிப்புத் தேற்றத்தின் ஒரு சிறப்புவகையாக ரோலின் தேற்றத்தைக் கருதலாம். டெயிலரின் தேற்ற நிறுவலுக்கும் ரோலின் தேற்றம் அடிப்படையாக அமைகிறது.
வரலாறு[தொகு]
முதன்முதலில் பிரெஞ்சு கணிதவியலாளர் மைக்கேல் ரோலால் 1691-ல் இத்தேற்றம் வகை நுண்கணித முறையில் நிறுவப்பட்டது. ரோலின் தேற்றம் என்ற பெயர், 1834-ல் ஜெர்மானிய கணிதவியலாளர் மோரிட்ஸ் வில்லெம் டுரோபிஷ் மற்றும் 1846-ல் இத்தாலிய கணிதவியலாளர் ஜியூஸ்டோ பெல்லாவிட்டில் ஆகிய இருவராலும் பயன்படுத்தப்பட்டது. [1]
எடுத்துக்காட்டுகள்[தொகு]

- சார்பு:
- r > 0
இச் சார்பின் வரைபடம், ஆதிப்புள்ளியை மையமாகக் கொண்ட வட்டத்தின் மேல் அரைவட்டப்பகுதி. இச்சார்பு,
- மூடிய இடைவெளி [−r,r] -ல் தொடர்ச்சியானது,
- திறந்த இடைவெளி (−r,r) -ல் வகையிடத்தக்கது,
ரோலின் தேற்றத்தின் மூன்று நிபந்தனைகளையும் இச்சார்பு சரிசெய்கிறது. எனவே தேற்ற முடிவின்படி (−r,r) -ல் ஏதாவது ஒரு மதிப்பிற்கு முதல்வகைக்கெழு பூச்சியமாகும்.
திறந்த இடைவெளியில் சார்பு வகையிடத்தக்கதாக இருந்தால் போதுமென இத்தேற்றம் கூறுவதால் இந்த எடுத்துக்காட்டின் சார்பு இடைவெளியின் முனைப்புள்ளிகளில் வகையிடத்தக்கதாக இல்லையென்றாலும் இத்தேற்றத்தைப் பயன்படுத்த முடிகிறது.

இச்சார்புக்கு, மூடிய இடைவெளி [-1 , 1]-ல் தொடர்ச்சியாக இருந்தாலும் x = 0 -ல் அதற்கு வகைக்கெழு இல்லை. x = 0 -ல் வகைக்கெழு பூச்சியமாகாமலேயே இருபுறமும் குறி மாறுகிறது. ரோலின் தேற்றத்தின் இரண்டாவது நிபந்தனை பூர்த்தியாகவில்லை. −1 , 1 -க்கிடையே எந்தவொரு புள்ளியிலும் முதல் வகைக்கெழு பூச்சியமாவதில்லை.
பொதுமைப்படுத்தல்[தொகு]
- ஒரு மெய்மதிப்புச் சார்பு. இச்சார்பு,
- மூடிய இடைவெளி [a,b]-ல் தொடர்ச்சியானதாகவும்,
- எனவும்
- ஒவ்வொரு -க்கும்
வலது எல்லை:
இடது எல்லை: ஆகிய இரண்டு எல்லைகளும் நீட்டிக்கப்பட்ட மெய்யெண் கோடு, [−∞, ∞] -ல் இருக்குமானால்,
- ஆகிய இரு எல்லைகளில் ஏதாவது ஒன்று ≥ 0 மற்றது ≤ 0 (நீட்டிக்கப்பட்ட மெய்யெண் கோட்டில்) ஆகவும் இருக்குமாறு ஏதாவது ஒரு மதிப்பு இருக்கும்.
- மேலும் இவ்விரண்டு எல்லைகளும் சமமாக இருப்பின் -க்கு வகைக்கெழு உண்டு. மேலும் அவ்வகைக்கெழு பூச்சியமாக இருக்கும்.
குறிப்பு:
- குழிவு அல்லது குவிவாக இருந்தால் இடைவெளியின் உள்ளே ஒவ்வொரு புள்ளியிலும் வலது மற்றும் இடது வகைக்கெழுக்கள் காணமுடியும். எனவே மேலே குறிப்பிட்ட இரு எல்லைகளும் காணக்கூடியதாகவும் மெய்யெண் மதிப்புடையவையாகவும் இருக்கும்.
- ஒரு பக்க (வலது அல்லது இடது) வகைக்கெழுக்கள் கூடும் சார்பாக அமைந்தால், ஒரு சார்பின் குவிவுத்தன்மையை நிறுவ பொதுமைப்படுத்தப்பட்ட ரோலின் தேற்றம் போதுமானதாக இருக்கும்.:[2]
பொதுமைப்படுத்தப்பட்ட தேற்றத்தின் நிறுவல்[தொகு]
இருவகையான ரோலின் தேற்றத்தின் நிறுவல்களும் கிட்டத்தட்ட ஒரேமாதியானவை என்பதால் பொதுமைப்படுத்தப்பட்ட வகைக்கான நிறுவலைக் காணலாம்.
- மூடிய இடைவெளி [a,b] -ல் தொடர்ச்சியானது என்பதால், அறுதி மதிப்புத் தேற்றத்தின்படி சார்புக்கு இந்த இடைவெளியில் குறைந்த பட்சம் ஒரு பெருமம் மற்றும் சிறுமம் இருக்கும்.
- பெருமம் மற்றும் சிறுமம் இரண்டும் இடைவெளியின் முனைப் புள்ளிகளில் அமைந்தால் சார்பு [a,b] -ல் மாறிலிச் சார்பாகும். எனவே (a,b) -ல் உள்ள ஒவ்வொரு புள்ளியிலும் -ன் வகைக்கெழு பூச்சியம்.
- பெருமம் இடைவெளியினுள் அமைகிறது என்க. -ல் பெருமம். (சிறுமத்திற்கும் இதேபோல் கொண்டு நிறுவலாம்).
ஏதேனும் ஒரு மெய்யெண் h-க்கு , எனில், -ன் மதிப்பு -ன் மதிப்பைவிடச் சிறியதாக இருக்கும்.
h > 0 எனில்:
- ஃ ...........1
இந்த எல்லை மதிப்பு -∞,ஆக அமையலாம்.
இதேபோல் h < 0, எனில்,
- ஃ ............2
இந்த எல்லை மதிப்பு ∞, ஆக அமையலாம்.
இறுதியாக இவ்விரண்டு எல்லைகளும் சமமாக இருந்தால் -ன் வகைக்கெழு c-ல் பூச்சியமாக இருக்கும். எனவே தேற்றம் நிறுவப்படுகிறது.
உயர்வரிசை வகைக்கெழுக்களுக்குப் பொதுமைப்படுத்தல்[தொகு]
சார்பு
- மூடிய இடைவெளி [a,b] -ல் n − 1 தடவைகள் தொடர்ச்சியாக வகையிடத்தக்கதாகவும்,
- திறந்தஇடைவெளி (a,b) -ல் nம் வகைக்கெழு காணமுடியக்கூடியதாகவும்,
- [a,b] -ன் a1 < b1 ≤ a2 < b2 ≤ . . .≤ an < bn -n உள் இடைவெளிகளில், 1 முதல் n வரையிலான ஒவ்வொரு k -க்கும்
எனவும் இருந்தால்:
- -ன் nம் -ஆம் வகைக்கெழு பூச்சியமாக இருக்குமாறு ஒரு மதிப்பு, இருக்கும்.
நிறுவல்[தொகு]
கணிதத் தொகுத்தறிதல் முறையில் இதனை நிறுவலாம்.
n = 1 எனில் இத்தேற்றம், ஏற்கனவே நிறுவப்பட்ட ரோலின் தேற்றத்தின் திட்ட வகையாகிவிடுவதால், உண்மையாகிறது.
எனவே இப்பொழுது இத்தேற்றம் n > 1 -க்கு உண்மையாகும் என நிறுவ வேண்டும்.
ரோலின் தேற்றத்தின் திட்ட வகையின் முடிவிலிருந்து 1 லிருந்து n வரையுள்ள ஒவ்வொரு முழு எண் k -க்கும், என்றவாறு இருக்கும்.
[c1,c2], . . .[cn−1,cn] -ஆகிய (n- 1) மூடிய இடைவெளிகளில் தேற்ற நிபந்தனைகளை நிறைவு செய்வதால், கணிதத் தொகுத்தறிதலின் கொள்கைப்படி, -ல் -ன் (n − 1)ம் -ஆம் வகைக்கெழு பூச்சியமாக இருக்கும்.
மேற்கோள்கள்[தொகு]
- ↑ See Florian Cajori's A History of Mathematics, p. 224 [1].
- ↑ Artin, Emil (1964) [1931], The Gamma Function, trans. Michael Butler, Holt, Rinehart and Winston, pp. 3–4
- Kaplansky, Irving (1972), Fields and Rings
- Craven, Thomas; Csordas, George (1977), "Multiplier sequences for fields", Illinois J. Math., 21 (4): 801–817
- Ballantine, C.; Roberts, J. (2002), "A Simple Proof of Rolle's Theorem for Finite Fields", The American Mathematical Monthly, Mathematical Association of America, 109 (1): 72–74, எண்ணிம ஆவணச் சுட்டி:10.2307/2695770, JSTOR 2695770
{{citation}}: Unknown parameter|month=ignored (|date=suggested) (help)





![{\displaystyle f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/993978def4799776b3421d0f286192f5eaf05442)

![{\displaystyle f(x)=|x|,\qquad x\in [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/106570318bb857ac95a60c075c30a0f40dde84fe)




















