வீட்ஸ்டன் சமனச்சுற்று
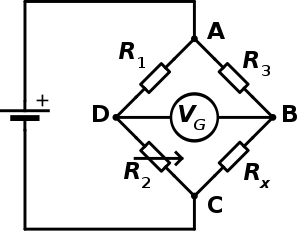
வீட்சுடன் சமனச்சுற்று, வீட்ஸ்டன் சமனி அல்லது வீட்ஸ்டன் பாலம் (Wheatstone Bridge) என்பது மின்தடையினை அளவிடப் பயன்படும் மின்கடத்திகளாலான ஓர் எளிய மின்சுற்றாகும். இது சாமுவேல் ஹன்ட்டர் கிறிஸ்டி என்பவரால் 1833ம் ஆண்டு கண்டுபிடிக்கப்பட்டது. பின் 1843ல் இதனை மேம்படுத்திப் பரவலாகச் செய்தவர் சர் சார்லஸ் வீட்ஸ்டன் ஆவார். முதலில் கண்டுபிடிக்கப்பட்ட பொழுது மண்ணை ஆராய்வதற்கும் ஒப்பிடுவதற்குமே இது மிகவும் பயன்பட்டது.
செயல்முறை[தொகு]
இச்சமனசுற்றில் நான்கு மின்தடையங்கள் , , மற்றும் ஒரு மூடிய சுற்றை உருவாக்கும்படிப் படத்தில் காட்டியவாறு இணைக்கப்பட்டுள்ளன. இங்கு என்னும் மின்தடையத்தின் மின்தடை அளவு தெரியாததாகும். மற்ற மின்தடையங்களின் அளவுகள் தெரிந்ததே. இவற்றுள் என்பது, தக்கவாறு மாற்றிக் கொள்ளக் கூடிய மின்தடை ஆகும்.
இச்சுற்றில் ஒரே கிளையில் உள்ள மின்தடைகளின் தகவுகள் மற்றும் சரிசமமாக இருக்கும்போது B மற்றும் D புள்ளிகளுக்கு இடையிலான மின்னழுத்த வேறுபாடு சுழியமாக இருக்கும். அச்சமயத்தில் கால்வனோமானியின் வழியே மின்னோட்டம் பாயாது. மின்காட்டியில் முள் விலக்கமுறாமல் இருக்கும். இதுவே சுற்றின் சமநிலை எனப்படும்.
மின்தடையம் வின் மின்தடை அளவினைத் தகுந்தவாறு மாற்றியமைப்பதின் மூலம் இத்தகைய சமநிலையினை அடைய இயலும்.
சுற்று சமநிலையில் உள்ளபோது
இச்சமன்பாட்டின் துணையுடன் தெரியாத மின்தடை ஒன்றின் அளவை() மிக எளிதாகக் கணக்கிட முடியும்.
கிர்க்காஃப் விதிகளின்படி விளக்கம்[தொகு]

மின்கலத்திலிருந்து வெளிப்படும் மின்னோட்டம் , , , என நான்கு பகுதிகளாகப் பிரிகிறது. கால்வனோமானியின் வழியே பாயும் மின்னோட்டம் ஆகும்.
கிர்க்காஃப் மின்னோட்ட விதியை B மற்றும் D சந்திகளுக்குப் பயன்படுத்துவதன் மூலம் கீழ்க்காணும் சமன்பாடுகள் பெறப்படுகின்றன.
கிர்க்காஃப் மின்னழுத்த விதியை மூடப்பட்ட பாதைகளான ABD மற்றும் BCD ஆகியவற்றிற்குப் பயன்படுத்துவதன் மூலம் கீழ்க்காணும் சமன்பாடுகள் பெறப்படுகின்றன.
சுற்று சமநிலையில் உள்ளபோது = 0 ஆகும். எனவே மின்னழுத்த விதி மூலம் மேலே பெறப்பட்ட சமன்பாடுகளைக் கீழ்க்காணும் முறையில் மாற்றியமைக்கலாம்.
மேற்கண்ட சமன்பாடுகளைப் பிரித்து மாற்றி அமைக்கும் போது இச்சமன்பாடு பெறப்படுகிறது.
மின்னோட்ட விதியின்படி , என்பதால், இவ்வாறு பெறப்படுகிறது.
பயன்பாடுகள்[தொகு]
வீட்ஸ்டன் சமனச்சுற்றுகள் அளவுக்கருவியியிலில்(instrumentation) இன்றியமையாததாகத் திகழ்கின்றன. விகாரமானிகள் (strain gauges), மின்தடை வெப்பமானி (resistance thermometer) மற்றும் பிற உணரிகள் (sensors), பண்புப்பெயர்ப்பிகள் (transducers) ஆகியவற்றுடன் ஓர் அங்கமாக இவை விளங்குகின்றன.
புவித்தொடுப்பு (earthing) சார்ந்த சோதனைகளிலும்(Murray loop test) வீட்ஸ்டன் சமனச்சுற்றுகள் பயன்படுகின்றன.
மீட்டர் சமனச்சுற்று, மின்னழுத்த வேறுபாட்டை அளவிடப் பயன்படும் மின்னழுத்தமானி(Pontentiometer) ஆகியவை வீட்ஸ்டன் சுற்றின் மற்றொரு வடிவமே ஆகும்.
வீட்ஸ்டன் சுற்றில் சில மாற்றங்களைச் செய்வதன் மூலம் மின்தூண்டம், மின்தேக்கம், மின்னெதிர்ப்பு, அலைவெண் ஆகியவற்றை அளவீடு செய்யும் சுற்றுகளையும் உருவாக்க முடியும். எரியத்தக்க வாயுக்களின் அளவைக் கணக்கெடுக்கும் எக்ஸ்புளோசிமீட்டர் கருவியையும் உருவாக்க முடியும்.
வீட்ஸ்டன் சமனச்சுற்றிலிருந்து வருவிக்கப்பட்ட பிற சுற்றுகள்[தொகு]
1865ல் ஜேம்ஸ் கிளார்க் மக்ஸ்வெல், வீட்ஸ்டன் சுற்றை அடிப்படையாகக் கொண்டு மாறுதிசை மின்சாரம் சார்ந்த அளவீட்டுச்சுற்றுகளை உருவாக்கினார். அவற்றை 1926ல் ஆலன் புளூம்லெய்ன் மேலும் மேம்படுத்தினார்.
மிகச்சிறிய அளவிலான மின்தடைகளை அளவீடு செய்யக்கூடிய சுற்றுகள் கெல்வின்(Kelvin) சமனச்சுற்று, கேரீ ஃபோஸ்டர்(Carey Foster) சமனச்சுற்று போன்றவை ஆகும்.
மின்தூண்டத்தை அளக்கக்கூடிய சமனச்சுற்று மேக்ஸ்வெல்(Maxwell) சமனச்சுற்று ஆகும். மின்தேக்கத்தை அளக்கக்கூடிய சமனச்சுற்று செர்ரிங்(Schering) சமனச்சுற்று ஆகும். அலைவெண்ணை அளக்கப் பயன்படுவது வியன்(Wien) சமனச்சுற்று ஆகும்.
வெளியிணைப்புகள்[தொகு]
- Wheatstone Bridge - Interactive Java Tutorial பரணிடப்பட்டது 2010-06-10 at the வந்தவழி இயந்திரம் National High Magnetic Field Laboratory
- efunda Wheatstone article
- Methods of Measuring Electrical Resistance - Edwin F. Northrup, 1912, full-text on Google Books
- Measuring strain using Wheatstone bridge principles பரணிடப்பட்டது 2014-12-18 at the வந்தவழி இயந்திரம்



















