முப்படியச் சார்பு

முப்படியச் சமன்பாடு உடன் குழப்பிக் கொள்ளாதீர்கள்.

மூன்று [[மெய்யெண்]] மூலங்களைக் கொண்ட கனச் செயல்பாட்டின் வரைபடம் (வளைவரை கிடைமட்ட அச்சைக் கடக்கும் இடம், y = 0 ). மேலே காட்டப்பட்ட வளைவரை இரண்டு [[மாறுநிலை எண்|மாறுநிலைப் புள்ளிகளைக்]] கொண்டுள்ளது. இதன் சார்பு: f(x) = (x³ + 3x² − 6x − 8)/4 .

கணிதத்தில், முப்படியச் சார்பு (Cubic function) என்பது $f(x)=ax^{3}+bx^{2}+cx+d,$ வடிவிலமைந்த சார்பாகும். அதாவது, மூன்றாம் படி பல்லுறுப்புக்கோவைச் சார்பு. . பல நூல்களில், குணகங்கள் a, b, c, மற்றும் d ஆகியவற்றை மெய்யெண்களாகக் கொண்டு, ஒரு மெய்யெண் சார்பாக, மெய்யெண் கணத்திலிருந்து மெய்யெண் கணத்திற்கு அல்லது சிக்கலெண் சார்பாக சிக்கலெண் கணத்திலிருந்து சிக்கலெண் கணத்திற்கும் வரையறுக்கப்படுகிறது. வேறு சிலவற்றில் குணகங்களைச் சிக்கலெண்களாகக் கொண்டு மெய்யெண் கணத்திலிருந்து மட்டுமே சிக்கலெண்கள் கணத்திற்கு வரையறுக்கப்படும் சிக்கலெண் சார்பாக எடுத்துக்கொள்ளப்படுகிறது. அதாவது இரண்டாவதில் சார்பின் ஆட்களம் மெய்யெண் கணமாக மட்டுமே இருந்து இணையாட்களம் சிக்கலெண் கணமாக அமைகிறது.

f(x) = 0 எனக் கொண்டால் கீழ்வரும் முப்படியச் சமன்பாடு கிடைக்கிறது:

$ax^{3}+bx^{2}+cx+d=0,$

மெய்யெண் குணகங்களைக் கொண்ட முப்படியச் சார்புக்கு ஒன்று அல்லது மூன்று மெய்யெண் மூலங்கள் உண்டு (அவை வெவ்வேறானவையாக இருக்க வேண்டியதில்லை); மெய்யெண் குணகங்களைக் கொண்ட அனைத்து ஒற்றையெண் படியுள்ள அனைத்து பல்லுறுப்புக்கோவைகளுக்கும் குறைந்தபட்சம் ஒரு மெய்யெண் மூலம் இருக்கும்.

ஒரு முப்படியச் சார்பின் வரைபடம் எப்போதும் ஒரேயொரு வளைவு மாற்றப்புள்ளியைக் கொண்டுள்ளது. இது இரண்டு மாறுநிலைப் புள்ளிகள், ஒரு இடஞ்சார் பெருமம், ஒரு இடஞ்சார் சிறுமம் கொண்டிருக்கலாம்; . இல்லையெனில், ஒரு முப்படியச் சார்பு ஓரியல்பானதாக இருக்கும். முப்படியச் சமன்பாட்டின் வரைபடம் அதன் வளைவுமாற்றப் புள்ளியைப் பொறுத்து சமச்சீராக இருக்கும்; அதாவது, இந்தப் புள்ளியைப் பொறுத்த அரைத் திருப்ப சுழற்சியின்கீழ் வரைபடம் எந்த மாற்றமும் அடையாது.

முப்படிய இடைக்கணிப்பிற்கு முப்படியச் சமன்பாடு அடிப்டையாக அமையும்.

வரலாறு

x3 − 3x2 − 144x + 432 (கருப்புக் கோடு) என்ற முப்படியச் சார்பின் மூலங்கள், நிலைப்புள்ளிகள், வளைவுமாற்றப் புள்ளி, குழிவு, முதலாம், இரண்டாம் வகைக்கெழுகள் (சிவப்பு, நீலம்).

ஒரு முப்படியச் சார்பின் மாறுநிலைப் புள்ளிகள் அதன் நிலைப் புள்ளிகள் ஆகும், அதாவது சார்பின் சாய்வு பூச்சியமாக இருக்கும் புள்ளிகள். முப்படியச் சார்பு f இன் மாறுநிலைப் புள்ளிகள் பின்வருமாறு வரையறுக்கப்படுகின்றன.

f(x) = ax³ + bx² + cx + d இன் வகைக்கெழு $3ax^{2}+2bx+c=0$ ஆக உள்ள சமன்பாட்டிலிருந்து பெறப்படும் x இன் மதிப்புகளில் மாறுநிலைப் புள்ளிகள் அமையும்.

மேற்படி இருபடிச் சமன்பாட்டில், இருபடி சூத்திரத்தைப் பயன்படுத்தக் கிடைக்கும் தீர்வுகள்:

$x_{\text{critical}}={\frac {-b\pm {\sqrt {b^{2}-3ac}}}{3a}}.$

வர்க்க மூலத்திற்குள் உள்ள குறி, மாறுநிலைப் புள்ளிகளின் எண்ணிக்கையை தீர்மானிக்கிறது.

• நேர்மமாக இருந்தால், இரண்டு மாறுநிலை புள்ளிகள் உள்ளன, ஒன்று இடஞ்சார் பெருமமாகவும் மற்றது இடஞ்சார் சிறுமமாகவும் இருக்கும்.
• b² – 3ac = 0 எனில், ஒரேயொரு மாறுநிலைப் புள்ளி மட்டுமே இருக்கும், அது ஒரு வளைவுமாற்றப் புள்ளி
• b² – 3ac < 0 எனில், (மெய்) மாறுநிலைப் புள்ளிகள் எதுவும் இல்லை.

பிந்தைய இரண்டு நிகழ்வுகளில், அதாவது, b² – 3ac நேர்மமாக இருந்தால், முப்படியச் சார்பு கண்டிப்பாக ஓரியல்புச் சார்பு ஆகும். (Δ₀ > 0 என்பதற்கு எடுத்துக்காட்டாகப் படத்தைக் காணவும்)

ஒரு சார்பு அதன் வளைவுமாற்றப் புள்ளியில் குழிவுத்தன்மையை மாற்றுகிறது. மேலும் அப்புள்ளியில், சார்பின் இரண்டாவது வகைக்கெழு பூச்சியமாகவும் மூன்றாவது வகைக்கெழு பூச்சியமற்றதாகவும் இருக்கும். எனவே ஒரு முப்படியச் சார்புக்கு எப்போதும் ஒரேயொரு வளைவுமாற்றப்புள்ளி இருக்கும்:

$x_{\text{inflection}}=-{\frac {b}{3a}}.$

வகைப்பாடு

$y=x^{3}+cx.$ வடிவ முப்படியச் சார்புகள் கன செயல்பாடுகள். எந்தவொரு முப்படியச்ச் சார்பின் வரைபடமும் இதுபோன்ற வளைவரைக்கு வடிவொத்ததாக இருக்கும்.

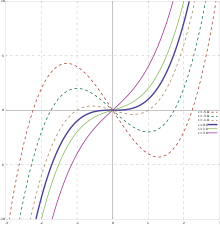
எல்லா முப்படிய வளைவரைகளும் ஒரு முப்படியச் சார்பைக் குறிக்காவிட்டாலும், ஒரு முப்படியச் சார்பின் வரைபடம் ஒரு முப்படிய வளைவரையாகும்.

முப்படியச் சார்புகள் நான்கு அளவுருக்களைச் சார்ந்திருந்தாலும், அவற்றின் வரைபடம் மிகக் குறைவான வடிவங்களை மட்டுமே கொண்டிருக்கும். உண்மையில், ஒரு முப்படியச் சார்பின் வரைபடம் எப்போதும் பின்வரும் சார்பின் வரைபடத்தை ஒத்திருக்கும்:

$y=x^{3}+px.$

சமச்சீர்மை

$y=x^{3}+px,$ வடிவ முப்படியச் சார்புகளின் வளைவுமாற்றப் புள்ளிகள் ஆதிப்புள்ளியாக இருக்கும். மேலும் இத்தகைய சார்பு [[ஒற்றைச் சார்பு|ஒற்றைச் சார்பாக]] இருக்குமென்பதால் ஆதிப்புள்ளியைப் பொறுத்து வரைபடம் சமச்சீர்மையுடையதாகவும் அரைத் திருப்பச் சுழற்சியில் மாற்றமில்லாமலும் இருக்கும். இந்த பண்புகள் வடிவொப்புமையால் மாறாதவையாக இருப்பதால், பின்வருபவை அனைத்தும் முப்படியச் சமன்பாடுகளுக்குப் பொருந்தும்.

வளைவுமாற்றப் புள்ளியைப் பொறுத்து முப்படியச் சார்பின் வரைபடம் சமச்சீர்மையுடையதாகவும் அரைத் திருப்பச் சுழற்சியில் மாறாதததாகவும் இருக்கும்.

வெளி இணைப்புகள்

விக்கிமீடியா பொதுவகத்தில்,
முப்படியச் சார்புகள்
என்பதில் ஊடகங்கள் உள்ளன.

• Hazewinkel, Michiel, ed. (2001), "Cardano formula", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104
• History of quadratic, cubic and quartic equations on MacTutor archive.