இருபடி வாய்பாடு
அடிப்படை இயற்கணிதத்தில் இருபடி வாய்பாடு (quadratic formula) என்பது ஒரு இருபடிச் சமன்பாட்டின் தீர்வுகளைக் காண உதவும் வாய்பாடாகும். இந்த இருபடி வாய்பாடு மட்டுமின்றி ஒரு இருபடிச் சமன்பாடின் தீர்வுகளை காரணிப்படுத்துதல், வர்க்க நிரப்பி முறை, வரைபடம் போன்ற முறைகளிலும் கண்டுபிடிக்கலாம்.[1]
ஒரு இருபடிச் சமன்பாட்டின் பொதுவடிவம்:
- (x மாறி, a, b and c மாறிலிகள்; a ≠ 0)
இச்சமன்பாட்டின் தீர்வுகளைத் தரும் இருபடி வாய்பாடு:
கூட்டல்-கழித்தல் குறிகள் சமன்பாட்டிற்கு இரு தீர்வுகள் உள்ளதைக் காட்டுகிறது[2]
இரு தீர்வுகளையும் தனித்தனியாக எழுத:
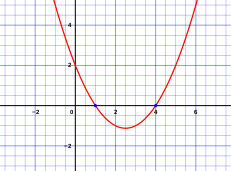
இவ்விரு தீர்வுகளும் இருபடிச் சமன்பாட்டின் வலப்புறமுள்ள பல்லுறுப்புக்கோவையின் மூலங்கள் என அழைக்கப்படுகின்றன. வடிவவியல்ரீதியாக இந்த மூலங்கள் y = ax2 + bx + c என்ற சமன்பாட்டின் வரைபடமாக அமையும் பரவளைவானது x-அச்சைச் சந்திக்கும் இரு புள்ளிகளின் x-மதிப்புகளைக் குறிக்கின்றன[3]
பரவளைவு x-அச்சைச் சந்திக்கும் புள்ளிகளை அறியத்தருவதோடு இவ்வாய்பாடு பரவளைவின் சமச்சீர் அச்சைக் காண்பதற்கும் பயன்படுகிறது.[4] மேலும் இவ்வாய்பாட்டினைக் கொண்டு இருபடிச் சமன்பாட்டிற்கு எத்தனை மெய்யெண் மூலங்கள் உள்ளன என்பதையும் தீர்மானிக்க முடிகிறது.[5]
வாய்பாட்டைத் தருவித்தல்[தொகு]
பல வழிகளில் இருபடி வாய்ப்பாட்டினைப் பெறலாம். அவற்றுள் எளியது வர்க்க நிரப்பி முறை ஆகும்.[6][7][8][9]
வர்க்க நிரப்பி முறை[தொகு]
- என்ற இயற்கணித வாய்ப்பாட்டைப் பயன்படுத்தி வர்க்க நிரப்பி முறையில் இருபடிச் வாய்ப்பாட்டைக் காணலாம்.[10]
வழி 1[தொகு]
இச்சமன்பாட்டை a -ஆல் வகுக்க, (a பூச்சியமல்லாததால் வகுத்தல் சாத்தியம்.)
அல்லது
- , பயன்படுத்த:
- வலதுபுறத்தில் பொதுவகுத்தியாக 4a2 -ஐக் கொள்ள:
- இருபுறமும் வர்க்கமூலம் காண:
வழி 2[தொகு]
வர்க்க நிரப்பி முறையை கீழ்க்காணும் வழியிலும் செய்யலாம்:[11]
- இருபுறமும் ஆல் பெருக்க வேண்டும்
- மாறியைச் சாரா உறுப்பை வலப்புறம் நகர்த்த வேண்டும்,
- இருபுறமும் ஐக் கூட்டிய பின்னர் இடப்புறத்தை முழு வர்க்கமாக மாற்றியெழுத வேண்டும்.
- பின்னர் இருபுறமும் வர்க்கமூலம் காண வேண்டும்.
- இறுதியில் ஐ மட்டும் இடப்புறத்தில் தனிமைப்படுத்தினால் வாய்பாடு கிட்டும்.
இது மிகவும் பழமையான வழிமுறையாகும். 1025 களிலேயே இந்தியாவில் இவ்வழிமுறை அறியப்பட்டிருந்தது.[12] வழி 1 ஐவிட குறைந்தளவு படிநிலைகளைக் கொண்டு இந்த இரண்டாம் வழிமூலம் இருபடிவாய்பாட்டை அடைய முடிகிறது. [11]
வழி 3[தொகு]
இச்சமன்பாட்டை a -ஆல் வகுக்க, (a பூச்சியமல்லாததால் வகுத்தல் சாத்தியம்.)
- எனப் பதிலிட:
- முதல் இரு உறுப்புகளுடன் ஐக் கூட்டி பின்னர் மூன்றாம் உறுப்பிலிருந்து அதைக் கழித்து, முதல் மூன்றையும் முழுவர்க்கமாக எழுத:
- இடப்புறத்தை இரு வர்க்கங்களின் வித்தியாசமாக எழுதிக் காரணிப்படுத்த:
அல்லது
அல்லது
இவற்றுக்கு என மறுபதிலிட இருபடி வாய்பாடு கிடைக்கிறது.
பதிலிடல் முறை[தொகு]
இருபடி வாய்பாடு காணும் மற்றொரு முறை பதிலிடல் முறையாகும்[13]
- எனப் பதிலிட:
- இதனை விரித்து இல் அமைந்த இருபடிச் சமன்பாடாக எழுத:
- இதில் உறுப்பு பூச்சியமாகும்வண்ணம் இன் மதிப்பை எடுத்தால்:
- அல்லது .
- இருபுறமும் மாறிலி உறுப்பைக் கழித்து ஆல் வகுக்க:
- இன் மதிப்பைப் பதிலிட:
- எனவே:
- மீண்டும் இன் மதிப்பை இன் வாயிலாகப் பதிலிட ( எனவே இருபடி வாய்பாடு கிடைக்கிறது:
இயற்கணித முற்றொருமைகளைப் பயன்படுத்தல்[தொகு]
இருபடி வாய்பாட்டைக் காண்பதற்குக் கீழ்க்காணும் முறை பல வரலாற்றுக் கணிதவியலாளர்களால் பயன்படுத்தப்பட்டுள்ளது.[14]
இருபடிச் சமன்பாட்டின் மூலங்கள் r1 மற்றும் r2.
முற்றொருமை:
இருபுறமும் வர்க்கமூலம் காண:
a ≠ 0 என்பதால் இருபடிச்சமன்பாட்டின் வலப்புறக்கோவையை a ஆல் வகுக்கக் கிடைக்கும் கோவை:
r1 மற்றும் r2 இக்கோவைக்கும் மூலங்களாக இருக்கும் என்பதால்:
இருபுறமும் ஒத்த உறுப்புகளின் குணங்களை ஒப்பிட:
இம்மதிப்புகளை இல் பதிலிட:
r2 = −r1 − ba என்பதால் மற்றும் எனப் பதிலிடக் கிடைக்கும் : இன் மதிப்புகள் முறையே:
இவற்றை இணைக்க இருபடிச் சமன்பாட்டின் தீர்வுகள்:
லாக்ரெஞ்சி கூறாக்கிகள் முறை[தொகு]
இருபடி வாய்ப்பாட்டைக் காணும் மற்றொரு முறை லாக்ராஞ்சி கூறாக்கிகள் முறையாகும்.(Lagrange resolvents]) இது கால்வா கோட்பாட்டின் ஆரம்பப் பகுதியாகும்.[15] இம்முறையானது, முப்படி பல்லுறுப்புக்கோவைகளுக்கும் நான்குபடி பல்லுறுப்புக்கோவைகளுக்கும் தீர்வு காணும் முறையைப் பொதுமைப்படுத்துகிறது. எனவே, ஒரு பல்லுறுப்புக்கோவையின் அடுக்கு எத்தனையாக இருந்தாலும் அக்கோவையின் மூலங்களின் சமச்சீர் குலத்தின் வாயிலாக அம்மூலங்களைப் பற்றித் தெரிந்துகொள்ள வழிவகுக்கும் கால்வாகோட்பாட்டிற்கு இது ஆரம்பமாக அமைகிறது. மூலங்களின் சமச்சீர் குலம் கால்வா குலம் எனப்படும்.
இந்த அணுகுமுறை மூலச்சமன்பாட்டின் வடிவத்தை மாற்றி அமைப்பதை விட மூலங்களின் மேல் அதிக கவனம் கொண்டுள்ளது.
- என்ற தலையொற்றை இருபடிப் பல்லுறுப்புக்கோவையை எடுத்துக் கொள்க.
அதன் காரணிகள்,
- எனக் கொள்க.
வலதுபுறத்தை விரித்தெழுத,
இங்கு
மற்றும்
பெருக்கலில் உறுப்புகளின் வரிசை அவசியமில்லாததால் α மற்றும் β இரண்டையும் அவற்றுக்குள்ளாக மாற்றுவதால் p மற்றும் q -ன் மதிப்புகள் மாறாது. p மற்றும் q இரண்டும் α , β -ல் அமைந்த சமச்சீர் பல்லுறுப்புக்கோவைகள் எனப்படும். அவை அடிப்படை சமச்சீர் பல்லுறுப்புக்கோவைகள் ஆகும். α, β -ல் அமைந்த எந்தவொரு பல்லுறுப்புக்கோவையையும் α + β மற்றும் αβ வாயிலாக எழுதலாம்.
பல்லுறுப்புக்கோவைகளைப் பகுப்பாய்தலுக்கும் தீர்ப்பதற்குமான கால்வா கோட்பாட்டின் அணுகுமுறை:
மூலங்களின் சமச்சீர் சார்புகளில் சமச்சீர்தன்மையை உடைத்து மூலங்களை மீளப்பெறமுடியக் கூடியவை எவை?
எனவே n படிகொண்ட பல்லுறுப்புக்கோவையைத் தீர்ப்பது என்பது, n எழுத்துக்களின் சமச்சீர் குலமான -லுள்ள n உறுப்புகளை வரிசைமாற்றப்படுத்தும் வழிகளுடன் தொடர்புடையதாகும். இருபடி பல்லுறுப்புக்கோவையில் இரு உறுப்புகளை வரிசைமாற்றுவது என்பது அவற்றை ஒன்றுக்கொன்று மாற்றிக் கொள்வதாகும். எனவே இருபடி பல்லுறுப்புக்கோவையைத் தீர்ப்பது எளிதானது.
மூலங்கள் α , β காண:
இவை பல்லுறுப்புக்கோவையின் லெக்ரெஞ்சி கூறாக்கிகள் எனப்படும். மூலங்களின் வரிசை இதில் மிகவும் முக்கியம். இச்சமன்பாடுகளைத் தீர்த்து மூலங்களைப் பெறலாம்:
முன்பு இக்கூறாக்கிகள் இரண்டாம் வரிசை கொண்ட தனித்த வூரியே மாற்று என அழைக்கப்பட்டன.(discrete Fourier transform (DFT) of order 2)
இம்மாற்றின் அணி வடிவம்:
இந்த அணியின் நேர்மாறு:
α , β -ல் அமைந்த சமச்சீர் சார்பாகும். எனவே அதை p , q வாயிலாக எழுத முடியும்.
இதில் α , β இரண்டையும் ஒன்றுக்கொன்று மாற்றக் கிடைப்பது:
ஃ சமச்சீர் சார்பு கிடையாது. எனவே மூலங்களின் சமச்சீர் சார்பாக அமையும் p , q வாயிலாக இதை எழுத முடியாது. எனினும் வரிசையை மாற்றுவதால் ல் ஏற்படும் மாற்றம் காரணி என்பதால்,
- என்பது மூலங்களின் சமச்சீர் சார்பாகும். இதை p , q வாயிலாக எழுதலாம்.
வர்க்கமூலம் காண,
- .
நேர்ம வர்க்க மூலத்தைமட்டும் எடுத்துக்கொண்டால்,
எனவே மூலங்கள்:
இதுவே இருபடி வாய்ப்பாடு.
- என பதிலிட தலையொற்றை அல்லாத வழக்கமான வடிவம் கிடைக்கும்.
கூறாக்கிகளைப் பின்வருமாறு கருதலாம்.
- : உச்சிப்புள்ளி.
- : தலையொற்றைப் பல்லுறுப்புக்கோவையின் தன்மைகாட்டி
வடிவவியல் பயன்பாடு[தொகு]

ஆயபகுமுறை வடிவவியலின் படி ஒரு இருபடி பல்லுறுப்புக்கோவையானது ஒரு பரவளைவைக் குறிக்கும். பரவளைவின் பொதுச் சமன்பாடு:
y =p(x) = y = ax² + bx + c
p ஒரு இருபடிக்கோவை, a, b, c மூன்றும் மாறிலிக் கெழுக்கள். இக்கோவையின் மூலங்கள் கோவையின் பரவளைவானது x-அச்சைச் சந்திக்கும் புள்ளிகளைக் குறிக்கின்றன. மேலும் இருபடி வாய்ப்பாட்டை இரு உறுப்புகளாகக் பிரித்தெழுத:
x = −b2a என்ற கோடு பரவளைவின் சமச்சீர் அச்சுக்கோடாகவும், √b2 − 4ac2a என்பது சமச்சீர் அச்சிலிருந்து , x-அச்சைச் சந்திக்கும் புள்ளிகளமையும் தொலைவைக் காட்டுகின்றன. கூட்டல் குறி சமச்சீர் அச்சிலிருந்து வலப்புறத் தொலைவையும் கழித்தல் குறி இடப்புறத் தொலைவையும் தருகின்றன.
தொலைவைக் குறிக்கும் பகுதி பூச்சியமானால், சமச்சீர் அச்சின் மதிப்பு மட்டுமே ஒரேயொரு தீர்வாக அமையும். அதாவது √b2 − 4ac = 0 அல்லது b2 − 4ac = 0 எனில் இருபடிச் சமன்பாட்டிற்கு ஒரேயொரு தீர்வு மட்டுமே உண்டு. அதாவது பரவளைவு x-அச்சை ஒரேயொரு புள்ளியில் மட்டுமே சந்திக்கும். √b2 − 4ac என்பது இருபடிச் சமன்பாட்டின் தீர்வுகளின் "தன்மைகாட்டி" என அழைக்கப்படுகிறது. தன்மைகாட்டியின் மதிப்பு:
- பூச்சியமாக இருந்தால் ஒரேயொரு தீர்வு உண்டு. அதாவது பரவளைவு x-அச்சை ஒரேயொரு புள்ளியில் மட்டுமே சந்திக்கும்.
- பூச்சியமற்றதாக, நேர்மமாக இருந்தால் இரு மெய்யெண் தீர்வுகள். பரவளைவு x-அச்சை இரு புள்ளிகளில் சந்திக்கும்.
- எதிர்மமாக இருந்தால் தீர்வுகள் சிக்கலெண்களாக இருக்கும். இச்சிக்கலெண் தீர்வுகள் ஒன்றுக்கொன்று இணையெண்களாக இருக்கும். பரவளைவு x-அச்சை சந்திக்கும் மெய்யெண் மதிப்புகள் கிடையாது.
வரலாறு[தொகு]
இருபடிச் சமன்பாட்டுக்குத் தீர்வுகாணும் பண்டைய முறைகள் வடிவவியல் வழிமுறைகளாக இருந்தன. பாபிலோனியர்களிடம் இருபடிச் சமன்பாடுகளைத் தீர்க்கும் கணக்குகளாகக் குறைக்கக்கூடிய கணக்குகள் காணப்படுகின்றன.[16] எகிப்திய பெர்லின் பாப்பிரசு மத்தியகால இராச்சிய காலத்தைச் சேர்ந்தது (கிமு 2050 - கிமு 1650). இதில் இரு உறுப்புகளைக் கொண்ட இருபடிச் சமன்பாட்டின் தீர்வு காணப்படுகிறது.[17]
கிரேக்கக் கணிதவியலாளர் யூக்ளிடு (circa 300 BC) தனது எலிமென்ட்சு புத்தகம் 2 இல் இருபடிச் சமன்பாடுகளைத் தீர்ப்பதற்கு வடிவவியல் முறைகளைப் பயன்படுத்தியிருக்கிறார்.[18] "கணிதக் கலையின் ஒன்பது அத்தியாயங்கள்" (The Nine Chapters on the Mathematical Art, கிமு 200) என்ற சீனப் படைப்பில் இருபடிச் சமன்பாடுகளின் விதிகள் உள்ளன.[19][20] கிரேக்கக் கணிதவியலாளர் டையோபண்டசு தனது "அரித்மெட்டிக்கா"வில் (கிபி 250) யூக்ளிடின் வடிவவியல் இயற்கணித முறையைவிட இயற்கணிதத்தை ஒத்த வழிமுறையில் இருபடிச் சமன்பாட்டிற்குத் தீர்வு கண்டுள்ளார்.[18] அவரது முறையில் இருபடிச் சமன்பாட்டிற்கு இரு நேர்மத் தீர்வுகள் இருந்தபோதும் ஒரு தீர்வுதான் கண்டுபிடிக்கப்பட்டது.[21]
இந்தியக் கணிதவியலாளர் பிரம்பகுப்தரின் (கிபி 597–668) படைப்பான பிரம்மசுபுட்தசித்தாந்தம் (Brāhmasphuṭasiddhānta) கிபி 628 இல் வெளியிடப்பட்டது. இந்நூலில் இருபடி வாய்பாடு காணப்படுகிறது.[22] ஆனால் குறியீடுகளுக்குப் பதிலாக சொற்களில் விளக்கப்பட்டுள்ளது.[23][24]
ஒன்பதாம் நூற்றாண்டின் பாரசீகக் கணிதவியலாளர் முகம்மது இப்னு மூசா அல்-குவாரிஸ்மி இருபடிச் சமன்பாட்டை இயற்கணித முறையில் தீர்வு கண்டுள்ளார்.[25] 1594 இல் சைமன் ஸ்டீவின் என்ற கணிதவியலாளர் இருபடி வாய்ப்பாட்டை முதலாவதாக அனைத்து வகைப்பாட்டுகளுடனும் கண்டுபிடித்தார்.[26] 1637 இல் ரெனே டேக்கார்ட் இருபடி வாய்பாட்டின் தற்போதைய வடிவில் சிறப்பு வகைகளுக்கான குறிப்புகளுடன் தனது புத்தகத்தில் (La Géométrie) வெளியிட்டார்.[27]
மேற்கோள்கள்[தொகு]
- ↑ "Quadratic Factorisation: The Complete Guide". Math Vault (in அமெரிக்க ஆங்கிலம்). 2016-03-13. பார்க்கப்பட்ட நாள் 2019-11-10.
- ↑ Sterling, Mary Jane (2010), Algebra I For Dummies, Wiley Publishing, p. 219, ISBN 978-0-470-55964-2
- ↑ "Understanding the quadratic formula". Khan Academy (in ஆங்கிலம்). பார்க்கப்பட்ட நாள் 2019-11-10.
- ↑ "Axis of Symmetry of a Parabola. How to find axis from equation or from a graph. To find the axis of symmetry ..." www.mathwarehouse.com. பார்க்கப்பட்ட நாள் 2019-11-10.
- ↑ "Discriminant review". Khan Academy (in ஆங்கிலம்). பார்க்கப்பட்ட நாள் 2019-11-10.
- ↑ Rich, Barnett; Schmidt, Philip (2004), Schaum's Outline of Theory and Problems of Elementary Algebra, The McGraw–Hill Companies, ISBN 0-07-141083-X, Chapter 13 §4.4, p. 291
- ↑ Li, Xuhui. An Investigation of Secondary School Algebra Teachers' Mathematical Knowledge for Teaching Algebraic Equation Solving, p. 56 (ProQuest, 2007): "The quadratic formula is the most general method for solving quadratic equations and is derived from another general method: completing the square."
- ↑ Rockswold, Gary. College algebra and trigonometry and precalculus, p. 178 (Addison Wesley, 2002).
- ↑ Beckenbach, Edwin et al. Modern college algebra and trigonometry, p. 81 (Wadsworth Pub. Co., 1986).
- ↑ Rich, Barnett; Schmidt, Philip (2004), Schaum's Outline of Theory and Problems of ELEMENTARY ALGEBRA, The McGraw-Hill Companies, ISBN 0-07-141083-X, Chapter 13 §4.4, p. 291
- ↑ 11.0 11.1 Hoehn, Larry (1975). "A More Elegant Method of Deriving the Quadratic Formula". The Mathematics Teacher 68 (5): 442–443. doi:10.5951/MT.68.5.0442. https://archive.org/details/sim_mathematics-teacher_1975-05_68_5/page/442.
- ↑ Smith, David E. (1958). History of Mathematics, Vol. II. Dover Publications. பக். 446. பன்னாட்டுத் தரப்புத்தக எண்:0486204308.
- ↑ Joseph J. Rotman. (2010). Advanced modern algebra (Vol. 114). American Mathematical Soc. Section 1.1
- ↑ Debnath, Lokenath (2009). "The legacy of Leonhard Euler – a tricentennial tribute". International Journal of Mathematical Education in Science and Technology 40 (3): 353–388. doi:10.1080/00207390802642237.
- ↑ Prasolov, Viktor; Solovyev, Yuri (1997), Elliptic functions and elliptic integrals, AMS Bookstore, ISBN 978 0 82180587 9, §6.2, p. 134
- ↑ Irving, Ron (2013). Beyond the Quadratic Formula. MAA. பக். 34. பன்னாட்டுத் தரப்புத்தக எண்:978-0-88385-783-0. https://books.google.com/books?id=CV_UInCRO38C&pg=PA39.
- ↑ The Cambridge Ancient History Part 2 Early History of the Middle East. Cambridge University Press. 1971. பக். 530. பன்னாட்டுத் தரப்புத்தக எண்:978-0-521-07791-0. https://books.google.com/books?id=slR7SFScEnwC&pg=PA530.
- ↑ 18.0 18.1 Irving, Ron (2013). Beyond the Quadratic Formula. MAA. பக். 39. பன்னாட்டுத் தரப்புத்தக எண்:978-0-88385-783-0. https://books.google.com/books?id=CV_UInCRO38C&pg=PA39.
- ↑ Aitken, Wayne. "A Chinese Classic: The Nine Chapters" (PDF). Mathematics Department, California State University. பார்க்கப்பட்ட நாள் 28 April 2013.
- ↑ Smith, David Eugene (1958). History of Mathematics. Courier Dover Publications. பக். 380. பன்னாட்டுத் தரப்புத்தக எண்:978-0-486-20430-7. https://archive.org/details/historyofmathema0002smit.
- ↑ Smith, David Eugene (1958). History of Mathematics. Courier Dover Publications. பக். 134. பன்னாட்டுத் தரப்புத்தக எண்:0-486-20429-4. https://archive.org/details/historyofmathema0002smit.
- ↑ Bradley, Michael. The Birth of Mathematics: Ancient Times to 1300, p. 86 (Infobase Publishing 2006).
- ↑ Mackenzie, Dana. The Universe in Zero Words: The Story of Mathematics as Told through Equations, p. 61 (Princeton University Press, 2012).
- ↑ Stillwell, John (2004). Mathematics and Its History (2nd ed.). Springer. பக். 87. பன்னாட்டுத் தரப்புத்தக எண்:0-387-95336-1.
- ↑ Irving, Ron (2013). Beyond the Quadratic Formula. MAA. பக். 42. பன்னாட்டுத் தரப்புத்தக எண்:978-0-88385-783-0. https://books.google.com/books?id=CV_UInCRO38C&pg=PA39.
- ↑ Struik, D. J.; Stevin, Simon (1958), The Principal Works of Simon Stevin, Mathematics (PDF), vol. II–B, C. V. Swets & Zeitlinger, p. 470
- ↑ Rene Descartes (in en). The Geometry. http://archive.org/details/TheGeometry.

























































































