கோட்டுருவியல்

கணிதத்தில், கோட்டுருவியல் (graph theory) என்பது கோட்டுருக்களைப் பற்றிய ஆய்வு ஆகும். கோட்டுருக்கள், பொருள்களுக்கு இடையிலான சோடிவரிசை உறவுகளை மாதிரிப்படுத்த உதவும் கணிதக் கட்டமைப்புகள் ஆகும். கோட்டுருக்கள் முனைகள் என அழைக்கப்படும் புள்ளிகளாலும், விளிம்புகள் என அழைக்கப்பயும் இரு முனைகளை இணைக்கும் விளிம்புகளாலும் ஆனது. முனைகள் "கணு"க்கள் என்றும் விளிம்புகள் "இணைப்பு"கள் அல்லது "கோடு"கள் எனவும் அழைக்கப்படுவதும் உண்டு. அடிப்படையில் திசையற்ற கோட்டுருக்கள் மற்றும் திசையுள்ள கோட்டுருக்களென இருவகைப்படுத்தப்படுகின்றன. திசையற்ற கோட்டுருக்களில் இரண்டு முனைகள் விளிம்புகளால் சமச்சீராக இணைக்கப்படுகின்றன. திசை கோட்டுருக்களில் இருமுனைகளை விளிம்புகள் அசமச்சீராக இணைக்கின்றன.
வரையறைகள்
[தொகு]கோட்டுருவியலின் வரையறைகள் வேறுபடுகின்றன. பின்வருபவை கோட்டுருக்கள் மற்றும் தொடர்புடைய கணித கட்டமைப்புகளை வரையறுக்கும் சில அடிப்படை வழிகளாகும்.
கோட்டுரு
[தொகு]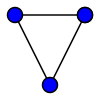
வழக்கமாகக் "கோட்டுரு" என்பது G = (V, E) என்ற வரிசைச் சோடியாகும்.[1][2] இதில்:
- V - "முனை"களின் கணம்
- E - விளிம்புகளின் கணம்
E ⊆ {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} என்பது வரிசையற்ற இரு வெவ்வேறு முனைகளாலான "விளிம்பு"களின் கணம்.
இக்கோட்டுருக்கள் "திசையற்ற எளிய கோட்டுருக்கள்" என அழைக்கப்படுகின்றன.
{x, y} என்ற விளிம்பில், x , y இரண்டும் விளிம்பின் இறுதிப்புள்ளிகள் எனப்படும். மேலும் இந்த விளிம்பானது x , y முனைகளை இணைக்கிறது அல்லது அம்முனைகளில் "படு"கிறது எனவும் x , y முனைகளின் "படுகை விளிம்பு" எனவும் அழைக்கப்படும்.
- பல்விளிம்புகள்
ஒரே வரிசைச் சோடி முனைகளை இணைக்கும் பல விளிம்புகள் பல இருக்குமானால் அவை "பல்விளிம்புகள் (கோட்டுருவியல்)" எனப்படுகின்றன.
- பல்கோட்டுருக்கள்
பல்விளிம்புகளைக் கணக்கில் கொள்வதற்காகக் கோட்டுருவானது ஒரு வரிசை மும்மையாக G = (V, E, ϕ) வரையறுக்கப்படுகிறது:[3][4]
ϕ: E → {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} என்பது ஒவ்வொரு விளிம்பையும் ஒரு வரிசையற்ற சோடி முனைகளுடன் (வெவ்வேறான இரு முனைகள்)கோர்க்கும் "படுகைச் சார்பு" (incidence function) ஆகும்.
குழப்பம் தவிர்க்க முதல் வகையான கோட்டுருக்கள் "திசையற்ற எளிய கோட்டுரு"க்கள் எனவும் பல்விளிம்புகளுடைய கோட்டுருக்கள் "திசையற்ற பல்கோட்டுருக்கள்" எனவும் அழைக்கப்படுகிறன.
- கண்ணி
ஒரு முனையை அதனுடனேயே இணைக்கும் விளிம்பானது கண்ணி என அழைக்கப்படும். மேலே தரப்பட்ட இரு வரையறைகளில் கண்ணிகள் இருக்க முடியாது. கண்ணிகள் அனுமதிக்கப்படுவதற்கு அவ்வரையறைகள் பின்னுள்ளவாறு நீட்டிக்கப்பட வேண்டும்.
திசையற்ற எளிய கோட்டுருக்களின் வரயறையிலுள்ள E ⊆ {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} என்பது E ⊆ {{x, y} | (x, y) ∈ V2} என நீட்டிக்கப்பட வேண்டும். இக்கோட்டுருக்கள் "கண்ணிகளை அனுமதிக்கும் திசையற்ற எளிய கோட்டுருக்கள்" எனக் குறிப்பிடப்படுகின்றன.
திசையற்ற பல்கோட்டுருக்கள் வரையறையிலுள்ள ϕ: E → {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} என்பது ϕ: E → {{x, y} | (x, y) ∈ V2} என நீட்டிக்கப்பட வேண்டும். இக்கோட்டுருக்கள் "கண்ணிகளை அனுமதிக்கும் திசையற்ற பல்கோட்டுருக்கள்" எனக் குறிப்பிடப்படுகின்றன.
- வரிசை, அளவு, படி
பொதுவாக V மற்றும் E ஆகிய இரண்டும் முடிவுற்ற கணங்களாகவே கொள்ளப்படுகின்றன. முடிவுறா கோட்டுருக்களுக்கு பல முடிவுகள் பொருத்தமற்றவையாகவும் வேறானவையாகவும் அமையும். கோட்டுருக்களில் பெரும்பாலும் முனைகளின் கணமான V வெற்றற்ற கணமாகக் கொள்ளப்படுகிறது. ஆனால் விளிம்புகளின் கணமான E வெற்றுக் கணமாக இருக்கலாம்.
- |V| ஆனது கோட்டுருவின் "வரிசை" எனவும் |E| ஆனது கோட்டுருவின் "அளவு" எனவும் அழைக்கப்படுகிறது.
- ஒரு முனையின் படுகை விளிம்புகளின் எண்ணிக்கை அம்முனையின் "படி" அல்லது "வலு" (degree or valency) எனப்படுகிறது. ஒரு முனையின் படியைக் கணக்கிடும்போது அதிலமையும் கண்ணி இருமுறை கணக்கிடப்படுகிறது.
- n வரிசையுடைய திசையற்ற எளிய கோட்டுருவில், ஒவ்வொரு முனையின் பெருமப் படி n − 1 ஆகவும் கோட்டுருவின் பெரும அளவு n(n − 1)/2 ஆகவும் இருக்கும்.
G என்ற கண்ணிகளை அனுமதிக்கும் திசையற்ற எளிய கோட்டுருவின் விளிம்புகள், G இன் முனைகளின் மீது "அடுத்தமையும் உறவை"த் தூண்டுகின்றன. ஒவ்வொரு விளிம்பு {x, y இன் இறுதிப்புள்ளிகள் x , y இரண்டும் அடுத்தடுத்த முனைகளாகும்; இது குறியீட்டில் x ~ y என எழுதப்படுகிறது.
திசை கோட்டுரு
[தொகு]
ஒரு கோட்டுருவின் ஒவ்வொரு விளிம்பும் திசையுடையதாக இருந்தால் அக்கோட்டுரு "திசை கோட்டுரு" அல்லது "திசையுள்ள கோட்டுரு" எனப்படும்.
திசை கோட்டுரு என்பது G = (V, E) என்ற வரிசைச் சோடிகளைக் குறிக்கும்:
- V - முனைகளின் கணம்;
E ⊆ {(x, y) | (x, y) ∈ V2 ∧ x ≠ y} - வரிசைச் சோடியாக அமையும் இரு வெவ்வேறான முனைகளை இணைக்கும் விளிம்புகளின் கணம். இவ்விளிம்புகள் திசை விளிம்புகள், திசை இணைப்புகள், அம்புகள் அல்லது விற்கள் எனவும் அழைக்கப்படுகின்றன. விளிம்புகளின் இறுதிமுனைகள் வெவ்வேறானவை.
இக்கோட்டுருக்கள் "திசையுள்ள எளிய கோட்டுருக்கள்" எனப்படுகின்றன.
(x, y) விளிம்பு x இலிருந்து y நோக்கி திசை கொண்டுள்ளது. x , y ஆகிய இருமுனைகளும் விளிம்பின் "இறுதிப்புள்ளிகள்" எனவும், x விளிம்பின் "வால்" மற்றும் y விளிம்பின் "தலை" எனவும் அழைக்கப்படுகின்றன. விளிம்பானது x , y முனைகளை இணைக்கிறது அல்லது அவற்றில் "படு"கிறது எனப்படுகிறது. (y, x) என்ற விளிம்பானது (x, y) விளிம்பின் நேர்மாறு விளிம்பாகும். எந்தவொரு விளிம்புடனும் இணைக்கப்படாத முனைகள் ஒரு கோட்டுருவில் இருக்கலாம். ஒரே தலை மற்றும் ஒரே வாலைக் கொண்ட விளிம்புகள் "பல்விளிம்புகள்"ஆகும்.
- திசையுள்ள பல்கோட்டுருக்கள்
பல்விளிம்புகளைக் கணக்கில் கொள்வதற்காகத் திசை கோட்டுருவானது ஒரு வரிசையுள்ள மும்மையாக G = (V, E, ϕ) வரையறுக்கப்படுகிறது:[3][5]
ϕ: E → {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} என்பது ஒவ்வொரு விளிம்பையும் ஒரு வரிசைச் சோடி முனைகளுடன் (வெவ்வேறான இரு முனைகள்)கோர்க்கும் "படுகைச் சார்பு" (incidence function) ஆகும்.
குழப்பம் தவிர்க்க முதல் வகையான கோட்டுருக்கள் "திசையுள்ள எளிய கோட்டுரு"க்கள் எனவும் பல்விளிம்புகளுடைய கோட்டுருக்கள் "திசையுள்ள பல்கோட்டுருக்கள்" எனவும் அழைக்கப்படுகிறன.
- கண்ணி
ஒரு முனையை அதனுடனேயே இணைக்கும் விளிம்பானது கண்ணி என அழைக்கப்படும். மேலே தரப்பட்ட இரு வரையறைகளில் கண்ணிகள் இருக்க முடியாது. கண்ணிகள் அனுமதிக்கப்படுவதற்கு அவ்வரையறைகள் பின்னுள்ளவாறு நீட்டிக்கப்பட வேண்டும்.
திசையுள்ள எளிய கோட்டுருக்களின் வரையறையிலுள்ள E ⊆ {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} என்பது E ⊆ {{x, y} | (x, y) ∈ V2} என நீட்டிக்கப்பட வேண்டும். இக்கோட்டுருக்கள் "கண்ணிகளை அனுமதிக்கும் திசையுள்ள எளிய கோட்டுருக்கள்" எனக் குறிப்பிடப்படுகின்றன.
திசையுள்ள பல்கோட்டுருக்கள் வரையறையிலுள்ள ϕ: E → {{x, y} | (x, y) ∈ V2 ∧ x ≠ y} என்பது ϕ: E → {{x, y} | (x, y) ∈ V2} என நீட்டிக்கப்பட வேண்டும். இக்கோட்டுருக்கள் "கண்ணிகளை அனுமதிக்கும் திசையுள்ள பல்கோட்டுருக்கள்" எனக் குறிப்பிடப்படுகின்றன.
கண்ணிகளை அனுமதிக்கும் திசையுள்ள எளிய கோட்டுருவின் விளிம்புகள், அக்கோட்டுருவின் முனைகளின் மீது "அண்மை உறவை"த் தூண்டுகின்றன. ஒவ்வொரு விளிம்பு {x, y} இன் இறுதிப்புள்ளிகள் x , y இரண்டும் "அடுத்தமையும் முனைகள்" அல்லது "அண்மை முனைகள்" ஆகும்; இவ்வுறவானது குறியீட்டில் x ~ y என எழுதப்படுகிறது.
கோட்டுரு வரைபடம்
[தொகு]கோட்டுருக்களின் முனைகளை புள்ளிகள் அல்லது சிறு வட்டங்களைக் கொண்டும் விளிம்புகளை இணைப்புள்ள முனைகளை இணைக்கும் கோடுகளைக் கொண்டும் வரைந்து ஒரு கோட்டுருவானது காட்சிப்படுத்தப்படுகிறது. கோட்டுரு திசையுள்ளதாக இருந்தால் அம்புக்குறிகள் மூலம் திசைகள் காட்டப்படுகின்றன.
ஒரு கோட்டுருவை பலவழிகளில் வரைந்து காட்சிப்படுத்த முடியுமென்பதால், கோட்டுருவின் வரைபடத்தை காட்சியற்ற நுண்புல அமைப்பான அக்கோட்டுருவுடன் குழப்பிக்கொள்ளக் கூடாது. ஒரு கோட்டுருவைப் பொறுத்தவரை, எந்தெந்த முனைகள் எந்தெந்த முனைகளோடு எத்தனை விளிம்புகளால் இணைப்புடையவை என்பதுதான் முக்கியமானதே தவிர அதன் வரைபடமல்ல. பெரும்பாலும் நடைமுறையில் இரு வரைபடங்கள் ஒரே கோட்டுருவுக்கானவையா இல்லையா என்பதைத் தீர்மானிப்பது கடினமானது. கோட்டுருக்களின் அமைவு களங்களைப் பொறுத்து சில வரைமுறைகள் மற்றவற்றைவிடச் சிறந்தவையாகவும் புரிந்துகொள்ள எளிதானவையாகவும் இருக்கலாம்.
வில்லியம். தா. தட்டு (W.T. Tutte) என்ற பிரித்தானியக் கணிதவியலாரின் முன்னோடி ஆய்வுகள் கோட்டுரு வரைதலுக்கு மிகவும் உதவியாகவுள்ளன. நேரியல் இயற்கணித முறைகளைக் கொண்டு கோட்டுரு வரைதலை அவர் அறிமுகப்படுத்தினார். தளமாக இல்லாத பிற மேற்பரப்புகளிலும் கோட்டுரு வரைதலுக்கான ஆய்வுகள் மேற்கொள்ளப்பட்டுகின்றன.
பயன்பாடுகள்
[தொகு]
இயற்பியல், உயிரியல், தகவற்துறை போன்ற பல துறைகளில் பல்வகையானத் தொடர்புகளையும் செய்முறைகளையும் மாதிரிப்படுத்தக் கோட்டுருக்கள் பயன்படுத்தப்படுகின்றன.[7][8] பல நடைமுறைக் கணக்குகளைக் கோட்டுருக்களைக் கொண்டு உருவகிக்கலாம். நடைமுறை உலக அமைப்புகளில் கோட்டுருக்களின் பயன்பாட்டை வலியுறுத்தும்விதமாக கோட்டுருவைக் குறிப்பதற்கு "வலையமைப்பு" (network) என்ற சொல் பயன்படுத்தப்படுகிறது.
மேற்கோள்கள்
[தொகு]- ↑ Bender & Williamson 2010, ப. 148.
- ↑ See, for instance, Iyanaga and Kawada, 69 J, p. 234 or Biggs, p. 4.
- ↑ 3.0 3.1 Bender & Williamson 2010, ப. 149.
- ↑ See, for instance, Graham et al., p. 5.
- ↑ See, for instance, Graham et al., p. 5.
- ↑ Hale, Scott A. (2013). "Multilinguals and Wikipedia Editing". Proceedings of the 2014 ACM Conference on Web Science - WebSci '14: 99–108. doi:10.1145/2615569.2615684. பன்னாட்டுத் தரப்புத்தக எண்:9781450326223. Bibcode: 2013arXiv1312.0976H.
- ↑ Mashaghi, A. (2004). "Investigation of a protein complex network". European Physical Journal B 41 (1): 113–121. doi:10.1140/epjb/e2004-00301-0. Bibcode: 2004EPJB...41..113M.
- ↑ Shah, Preya; Ashourvan, Arian; Mikhail, Fadi; Pines, Adam; Kini, Lohith; Oechsel, Kelly; Das, Sandhitsu R; Stein, Joel M et al. (2019-07-01). "Characterizing the role of the structural connectome in seizure dynamics" (in en). Brain 142 (7): 1955–1972. doi:10.1093/brain/awz125. பன்னாட்டுத் தர தொடர் எண்:0006-8950.
