எங்கிருந்து வந்தது சதுரம் (புதிர்)
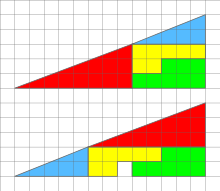
எங்கிருந்து வந்தது ஒரு சதுரம்? (Missing Square puzzle) என்பது ஒரு காட்சி மயக்க விளைவாகும் கணித வகுப்புக்களில் மாணவர்களுக்கு கேத்திர கணித உருக்களின் பண்புகளை தர்க்க ரீதியான சிந்தனை மூலம் விளங்கி கொள்ள பயன்படுத்தப்படுகின்ற ஒரு பிரசினமாகும். இங்கு இரண்டு செங்கோண முக்கோணங்கள், இரண்டு ஒழுங்கற்ற அறுகோணிகள் என நான்கு கேத்திர கணித உருக்கள் எடுத்துக் கொள்ளப்பட்டுள்ளன. இந்த நான்கு உருக்களையும் கொண்டு ஒரே அளவிலான (13 x 5) ஆனால் இரு வெவ்வேறு விதங்களில் இணைக்கப்பட்ட செங்கோண முக்கோணங்களாகத் தோற்றமளிக்கும் வடிவங்கள் ஒழுங்கமைக்கப்பட்டுள்ளன. ஆனால் அவற்றில் இரண்டாவதில் 1 x 1 எனும் ஒரு சதுரம் எஞ்சுகின்றது.
தீர்வு
[தொகு]

இந்த புதிருக்கான தீர்வுக்கு அடிப்படையாக அமைவது யாதெனில் இரண்டு 13 x 5 'செங்கோண முக்கோணங்களும்' உண்மையில் முக்கோணங்கள் இல்லை. ஏனெனில் அவற்றின் செம்பக்கங்கள் நேர்கோடுகளாக இல்லாமல் வளைவாக உள்ளன. சுருக்கமாகச் சொல்வதானால் நமது கண்களிற்கு 13 x 5 முக்கோணத்தின் சாய்வு ஒரே சீரானதாக இருப்பதாகத் தோன்றினாலும் உண்மையில் 13 x 5 முக்கோணத்தின் சாய்வு ஒரே சீரானதாக இல்லை. ஒரு 13 x 5 முக்கோணமானது மேற்படி அளவுகளில் உருவாக்கப்பட முடியாது.
நான்கு வடிவங்களின் (மஞ்சள், சிவப்பு, நீலம், பச்சை வண்ண வடிவங்கள்) உண்மையான மொத்தப் பரப்பு 32 சதுர அலகுகள்.
- சிவப்புச் செங்கோண முக்கோணத்தின் பரப்பு = 1/2 x 8 x 3 = 12
- நீலச் செங்கோண முக்கோணத்தின் பரப்பு = 1/2 x 5 x 2 = 5
- மஞ்சள் வடிவின் பரப்பு = 7
- பச்சை வடிவின் பரப்பு = 8
மொத்தப்பரப்பு = 12 + 5 + 7 + 8 = 32.
ஆனால் நம் கண்களுக்கு 13 x 5 அளவில் செங்கோண முக்கோணமாகத் தோற்றமளிக்கும் வடிவின் பரப்பு:
- அலகுகள்.
நீல நிற செங்கோண முக்கோணத்தின் பக்க விகிதம் 5:2 (=2.5:1),
சிவப்பு நிற செங்கோண முக்கோணத்தின் பக்க விகிதம் 8:3 (≈2.667:1),
இவ்விரண்டு விகிதங்களும் சமமில்லை.
எனவே எடுத்துக்கொள்ளப்பட்ட நான்கு வடிவங்களைக் கொண்டு அமைக்கப்பட்ட இருவிதமான அமைப்புகளிலும் செங்கோண முக்கோணங்களாகத் தோன்றும் வடிவங்களின் செம்பக்கங்கள் நேர்கோடாக இல்லாமல் உண்மையில் வளைவுடன் அமைகிறது.
இந்த வளைவின் அளவு கிட்டத்தட்ட ஒரு அலகில் 1/28 பங்காக (1.245364267°) இருக்கும். இதனால்தான் இந்த வளைவு கண்களுக்குத் தெரிவதில்லை.
படத்திலிருந்து இருவிதமான அமைப்பிலும், நீல மற்றும் சிவப்பு செம்பக்கங்கள் இரண்டும் ஒன்றின் மேலாக (அல்லது கீழாக) மற்றது என அமைகிறன. இதனால் கிடைக்கும் மெல்லிய இணைகரத்தைப் படத்தில் காணலாம். இந்த இணைகரத்தின் பரப்பு சரியாக, இரண்டாவது அமைப்பில் காணாமற்போன சதுரத்தின் (ஒரு கட்டம்) பரப்புக்குச் சமமாக இருக்கும்.
கணிதம் மற்றும் அறிவியல் எழுத்தாளரான மார்ட்டின் கார்டனரின் (அமெரிக்கா) கருத்துப்படி, 1953 இல் நியூயார்க் நகர பொழுதுபோக்கு மந்திரவாதியான பால் கர்ரி என்பவரால் இப்புதிர் கண்டறியப்பட்டது.[1] எனினும் 16 ஆம் நூற்றாண்டின் தொடக்கத்திலேயே கூறிடல் முரண்பாடு அறியப்பட்டிருந்தது.
இப்புதிரில் வரக்கூடிய முழு எண் அளவுகள் 2, 3, 5, 8, 13 பிபனாச்சி எண்கள். வேறு பல கூறிடல் புதிர்கள், ஃபிபனாச்சி எண்களின் எளிய பண்புகளின் அடிப்படையில் அமைந்துள்ளன.[2]
ஒத்த புதிர்கள்
[தொகு]புதிர்-1
[தொகு]
மேலே தரப்பட்டதைப் போன்ற மற்றுமொரு புதிர் இது. நான்கு சர்வசம நாற்கரங்களையும் ஒரு சிறு சதுரத்தையும் கொண்டு அமைக்கப்பட்ட ஒரு பெரிய சதுரத்தைக் கொண்டுள்ளது. நாற்கரங்களை அவற்றின் மையங்களைப் பொறுத்து சுழற்ற அவை நான்கும் சேர்ந்து நடுவிலுள்ள சிறு சதுரத்தையும் சேர்த்து அடைத்துக் கொண்டது போலத் தோற்றமளிக்கின்றன. எனவே நடுவில் அமைந்திருந்த சிறிய சதுரம் காணாமல் போய்விட்ட மாதிரி ஒரு மாயத் தோற்றம் ஏற்படுகிறது.
இதற்குக் காரணம் சுழற்சிக்கு முன்பும் பின்னரும் உள்ள பெரிய சதுரங்களின் பரப்பளவுகள் சமமாக உள்ளது போல் தோன்றினாலும், உண்மையில் சுழற்சிக்குப் பின் அமையும் பெரிய சதுரத்தின் பரப்பு முன்னதன் பரப்பைவிட சற்றே குறைவானதாக இருக்கும்.
பெரிய சதுரத்தின் பக்கம் a, ஒவ்வொரு நாற்கரத்தின் எதிரெதிர் பக்கங்களுக்கு இடையேயுள்ள கோணம் θ எனில்:
சுழற்சிக்கு முன்னும் பின்னும் உள்ள பெரிய சதுரங்களின் பரப்பளவுகளின் ஈவு sec2θ − 1. θ = 5° எனில், இதன் மதிப்புத் தோராயமாக 1.00765. எனவே இரு சதுரங்களின் பரப்பளவுகளுக்கு இடையேயுள்ள வித்தியாசம் 0.8% ஆக அமையும்.
புதிர்-2
[தொகு]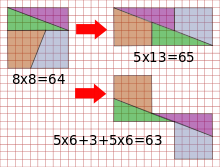
முதலிலுள்ள சதுர அமைப்பின் சிறு பகுதிகளைக் கொண்டு, இரண்டு வெவ்வேறுவிதமாக வடிவங்கள் உருவாக்கப்படுகின்றன. அவற்றில் பெரியதாக உள்ள அமைப்பில் பகுதிகளுக்கு இடையேயுள்ள இடைவெளிகள், மூலச் சதுர அமைப்பின் இடைவெளிகளைவிட ஒரு அலகு சதுரப் பரப்பளவை அதிகமாகவும், இரண்டாவது அமைப்பில் ஒன்று குறைவாகவும் கொண்டுள்ளதே இப்புதிரின் முரண்பாடு.
மேற்கோள்கள்
[தொகு]- ↑ Martin, Gardner (1956). Mathematics Magic and Mystery. Dover. pp. 139–150.
- ↑ Weisstein, Eric. "Cassini's Identity".
{{cite web}}: More than one of|author=and|last=specified (help)
வெளி இணைப்புகள்
[தொகு]- Missing Square variant காணொளி செய்விளக்கத்துடன்.
- Curry's Paradox: How Is It Possible? at cut-the-knot
- Triangles and Paradoxes at archimedes-lab.org
- The Triangle Problem or What's Wrong with the Obvious Truth பரணிடப்பட்டது 2007-06-21 at the வந்தவழி இயந்திரம்
- Jigsaw Paradox
- The Eleven Holes Puzzle
- Very nice animated Excel workbook of the Missing Square Puzzle
- Curry's Paradox and Area காணொளி விளக்கம்

