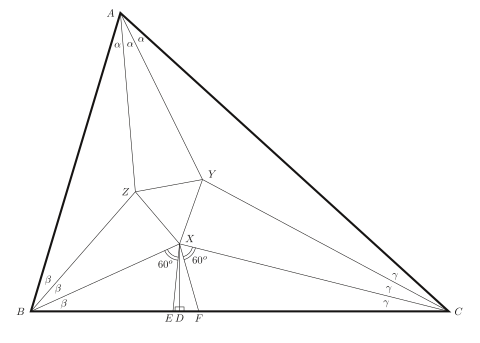
மோர்லியின் தேற்றப்படி, வெளி முக்கோணத்தின் ஒவ்வொரு உச்சிக்கோணத்தையும் முச்சமக் கூறிட்டால் செவ்வூதா நிற முக்கோணம் சமபக்க முக்கோணமாக இருக்கும். யூக்ளிடிய வடிவவியலில் எந்தவொரு முக்கோணத்தின் அடுத்தடுத்தமையும் கோண முச்சமவெட்டிகள் வெட்டிக்கொள்ளும் மூன்று புள்ளிகள், ஒரு சமபக்க முக்கோணத்தை அமைக்கும் என்று மோர்லியின் முச்சமவெட்டித் தேற்றம் (Morley's trisector theorem ) கூறுகிறது. அச்சமபக்க முக்கோணமானது "மோர்லி முக்கோணம்" என அழைக்கப்படுகிறது. இத் தேற்றம் 1899 ஆம் ஆண்டில் ஆங்கிலோ- அமெரிக்கக் கணிதவியலாளரான பிராங்க் மோர்லியால் கண்டறியப்பட்டது. எல்லா முச்சமவெட்டிகளும் வெட்டிக்கொண்டால் மேலும் நான்கு சமபக்க முக்கோணங்கள் கிடைக்கும்.
நிறுவல்கள் [ தொகு ] மோர்லியின் தேற்றத்திற்கு நுட்பமான சில நிறுவல்கள் உட்படப் பல நிறுவல்கள் உள்ளன.[1] முக்கோணவியல் கணக்கீடுகளைக் கொண்டிருந்தன. அண்மைக்கால நிறுவல்கள், பிரெஞ்சுக் கணிதவியலாளர் ஆலன் கானின் இயற்கணித நிறுவலையும்(Alain Connes (1998 , 2004 )) ஆங்கிலக் கணிதவியலாளர் ஜான் கான்வேயின் வடிவவியல் நிறுவலையும் கொண்டுள்ளன.[2] [3] [4]
Fig 1. மோர்லியின் முச்சமவெட்டித் தேற்றத்திற்கான நிறுவல் படம் எளிய நிறுவல் [ தொகு ] முக்கோணவியல் முற்றொருமையைப் பயன்படுத்தி மோர்லியின் தேற்ற நிறுவல்:
பயன்படுத்தப்படும் முக்கோணவியல் முற்றொருமை:
sin
(
3
θ
)
=
4
sin
θ
sin
(
60
∘
+
θ
)
sin
(
120
∘
+
θ
)
{\displaystyle \sin(3\theta )=4\sin \theta \sin(60^{\circ }+\theta )\sin(120^{\circ }+\theta )}
( 1 )
sin
(
3
θ
)
=
−
4
sin
3
θ
+
3
sin
θ
.
{\displaystyle \sin(3\theta )=-4\sin ^{3}\theta +3\sin \theta .}
முக்கோணம் ABC இன் பக்கம்
B
C
¯
{\displaystyle {\overline {BC}}}
D
,
E
,
F
{\displaystyle D,E,F}
3
α
+
3
β
+
3
γ
=
180
∘
{\displaystyle 3\alpha +3\beta +3\gamma =180^{\circ }}
⟹
α
+
β
+
γ
=
60
∘
.
{\displaystyle \implies \alpha +\beta +\gamma =60^{\circ }.}
△
X
E
F
{\displaystyle \triangle XEF}
∠
E
X
F
=
α
{\displaystyle \angle {EXF}=\alpha }
∠
X
E
F
=
(
60
∘
+
β
)
,
{\displaystyle \angle {XEF}=(60^{\circ }+\beta ),}
∠
X
F
E
=
(
60
∘
+
γ
)
.
{\displaystyle \angle {XFE}=(60^{\circ }+\gamma ).}
△
X
E
F
{\displaystyle \triangle XEF}
sin
(
60
∘
+
β
)
=
D
X
¯
X
E
¯
{\displaystyle \sin(60^{\circ }+\beta )={\frac {\overline {DX}}{\overline {XE}}}}
( 2 )
sin
(
60
∘
+
γ
)
=
D
X
¯
X
F
¯
.
{\displaystyle \sin(60^{\circ }+\gamma )={\frac {\overline {DX}}{\overline {XF}}}.}
( 3 )
மேலும்,
△
A
Y
C
,
{\displaystyle \triangle AYC,}
△
A
Z
B
{\displaystyle \triangle AZB}
∠
A
Y
C
=
180
∘
−
(
α
+
γ
)
=
180
∘
−
(
60
∘
−
β
)
=
120
∘
+
β
{\displaystyle \angle {AYC}=180^{\circ }-(\alpha +\gamma )=180^{\circ }-(60^{\circ }-\beta )=120^{\circ }+\beta }
∠
A
Z
B
=
120
∘
+
γ
.
{\displaystyle \angle {AZB}=120^{\circ }+\gamma .}
( 4 )
△
A
Y
C
{\displaystyle \triangle AYC}
சைன் விதியைப் பயன்படுத்த:
A
C
¯
sin
(
120
∘
+
β
)
=
A
Y
¯
sin
γ
{\displaystyle {\frac {\overline {AC}}{\sin(120^{\circ }+\beta )}}={\frac {\overline {AY}}{\sin \gamma }}}
⟹
sin
(
120
∘
+
β
)
=
A
C
¯
A
Y
¯
sin
γ
{\displaystyle \implies \sin(120^{\circ }+\beta )={\frac {\overline {AC}}{\overline {AY}}}\sin \gamma }
( 5 )
△
A
Z
B
{\displaystyle \triangle AZB}
சைன் விதியைப் பயன்படுத்த:
A
B
¯
sin
(
120
∘
+
γ
)
=
A
Z
¯
sin
β
.
{\displaystyle {\frac {\overline {AB}}{\sin(120^{\circ }+\gamma )}}={\frac {\overline {AZ}}{\sin \beta }}.}
sin
(
120
∘
+
γ
)
=
A
B
¯
A
Z
¯
sin
β
.
{\displaystyle \sin(120^{\circ }+\gamma )={\frac {\overline {AB}}{\overline {AZ}}}\sin \beta .}
( 6 )
A
B
C
{\displaystyle ABC}
h
{\displaystyle h}
h
=
A
B
¯
sin
(
3
β
)
=
A
B
¯
⋅
4
sin
β
sin
(
60
∘
+
β
)
sin
(
120
∘
+
β
)
{\displaystyle h={\overline {AB}}\sin(3\beta )={\overline {AB}}\cdot 4\sin \beta \sin(60^{\circ }+\beta )\sin(120^{\circ }+\beta )}
h
=
A
C
¯
sin
(
3
γ
)
=
A
C
¯
⋅
4
sin
γ
sin
(
60
∘
+
γ
)
sin
(
120
∘
+
γ
)
.
{\displaystyle h={\overline {AC}}\sin(3\gamma )={\overline {AC}}\cdot 4\sin \gamma \sin(60^{\circ }+\gamma )\sin(120^{\circ }+\gamma ).}
β
{\displaystyle \beta }
γ
{\displaystyle \gamma }
h
=
4
A
B
¯
sin
β
⋅
D
X
¯
X
E
¯
⋅
A
C
¯
A
Y
¯
sin
γ
{\displaystyle h=4{\overline {AB}}\sin \beta \cdot {\frac {\overline {DX}}{\overline {XE}}}\cdot {\frac {\overline {AC}}{\overline {AY}}}\sin \gamma }
h
=
4
A
C
¯
sin
γ
⋅
D
X
¯
X
F
¯
⋅
A
B
¯
A
Z
¯
sin
β
{\displaystyle h=4{\overline {AC}}\sin \gamma \cdot {\frac {\overline {DX}}{\overline {XF}}}\cdot {\frac {\overline {AB}}{\overline {AZ}}}\sin \beta }
h
{\displaystyle h}
X
E
¯
⋅
A
Y
¯
=
X
F
¯
⋅
A
Z
¯
{\displaystyle {\overline {XE}}\cdot {\overline {AY}}={\overline {XF}}\cdot {\overline {AZ}}}
X
E
¯
X
F
¯
=
A
Z
¯
A
Y
¯
.
{\displaystyle {\frac {\overline {XE}}{\overline {XF}}}={\frac {\overline {AZ}}{\overline {AY}}}.}
எனவே,
△
X
E
F
∼
△
A
Z
Y
{\displaystyle \triangle XEF\sim \triangle AZY}
வடிவொத்த முக்கோணங்கள் )வடிவொத்த முக்கோணங்களின் பண்பின்படி, அவற்றின் ஒத்த கோணங்கள் சமம்.
∠
A
Y
Z
=
∠
X
F
E
=
(
60
∘
+
γ
)
{\displaystyle \angle {AYZ}=\angle {XFE}=(60^{\circ }+\gamma )}
∠
A
Z
Y
=
∠
X
E
F
=
(
60
∘
+
β
)
.
{\displaystyle \angle {AZY}=\angle {XEF}=(60^{\circ }+\beta ).}
∠
B
X
Z
=
∠
C
Y
X
=
(
60
∘
+
α
)
{\displaystyle \angle {BXZ}=\angle {CYX}=(60^{\circ }+\alpha )}
படத்திலிருந்து
∠
A
Z
Y
+
∠
A
Z
B
+
∠
B
Z
X
+
∠
X
Z
Y
=
360
∘
{\displaystyle \angle {AZY}+\angle {AZB}+\angle {BZX}+\angle {XZY}=360^{\circ }}
இதில் தெரிந்த கோணங்களின் மதிப்புகளைப் பதிலிட்டுச் சுருக்க:
(
60
∘
+
β
)
+
(
120
∘
+
γ
)
+
(
60
∘
+
α
)
+
∠
X
Z
Y
=
360
∘
{\displaystyle (60^{\circ }+\beta )+(120^{\circ }+\gamma )+(60^{\circ }+\alpha )+\angle {XZY}=360^{\circ }}
⟹
∠
X
Z
Y
=
60
∘
.
{\displaystyle \implies \angle {XZY}=60^{\circ }.}
இதேபோல
△
X
Y
Z
{\displaystyle \triangle XYZ}
60
∘
.
{\displaystyle 60^{\circ }.}
△
X
Y
Z
{\displaystyle \triangle XYZ}
தேற்றம் நிறுவப்பட்டது.
பக்கமும் பரப்பளவும் [ தொகு ] முதல் மோர்லி முக்கோணத்தின் பக்க நீளம்:
a
′
=
b
′
=
c
′
=
8
R
sin
(
A
/
3
)
sin
(
B
/
3
)
sin
(
C
/
3
)
,
{\displaystyle a^{\prime }=b^{\prime }=c^{\prime }=8R\sin(A/3)\sin(B/3)\sin(C/3),\,}
[5] இதில் R என்பது மூல முக்கோணம் ABC இன் சுற்றுவட்ட ஆரம் .
பரப்பளவு:
ஒரு சமபக்க முக்கோணத்தின் பரப்பளவுக்கான வாய்பாடு:
A
=
3
4
a
′
2
,
{\displaystyle {\text{A}}={\tfrac {\sqrt {3}}{4}}a'^{2},}
A
=
16
3
R
2
sin
2
(
A
/
3
)
sin
2
(
B
/
3
)
sin
2
(
C
/
3
)
.
{\displaystyle {\text{A}}=16{\sqrt {3}}R^{2}\sin ^{2}(A/3)\sin ^{2}(B/3)\sin ^{2}(C/3).}
குறிப்புகள் [ தொகு ]
↑ Bogomolny, Alexander , Morley's Miracle Cut-the-knot , பார்க்கப்பட்ட நாள் 2010-01-02 ↑ Bogomolny, Alexander , J. Conway's proof Cut-the-knot , பார்க்கப்பட்ட நாள் 2021-12-03 ↑ Conway, John (2006), "The Power of Mathematics", in Blackwell, Alan; Mackay, David (eds.), Power (PDF) , Cambridge University Press, pp. 36–50, ISBN 978-0-521-82377-7 , பார்க்கப்பட்ட நாள் 2010-10-08 ↑ Morley's Theorem in Spherical Geometry , Java applet.↑ Weisstein, Eric W., "First Morley Triangle" , MathWorld .
மேற்கோள்கள் [ தொகு ] Connes, Alain (1998), "A new proof of Morley's theorem" , Publications Mathématiques de l'IHÉS , S88 : 43–46Connes, Alain (December 2004), "Symmetries" (PDF) , European Mathematical Society Newsletter54 Coxeter, H. S. M. ; Greitzer, S. L. (1967), Geometry Revisited , அமெரிக்கக் கணிதவியல் சங்கம் , LCCN 67-20607 Francis, Richard L. (2002), "Modern Mathematical Milestones: Morley's Mystery" (PDF) , Missouri Journal of Mathematical Sciences , 14 (1), doi :10.35834/2002/1401016 Guy, Richard K. (2007), "The lighthouse theorem, Morley & Malfatti—a budget of paradoxes" (PDF) , American Mathematical Monthly 114 (2): 97–141, doi :10.1080/00029890.2007.11920398 , JSTOR 27642143 , MR 2290364 , archived from the original (PDF) on 2010-04-01Oakley, C. O.; Baker, J. C. (1978), "The Morley trisector theorem", American Mathematical Monthly , 85 (9): 737–745, doi :10.2307/2321680 , JSTOR 2321680 Taylor, F. Glanville; Marr, W. L. (1913–14), "The six trisectors of each of the angles of a triangle", Proceedings of the Edinburgh Mathematical Society , 33 : 119–131, doi :10.1017/S0013091500035100 வெளியிணைப்புகள் [ தொகு ]