ஆள்கூற்று முறைமை
ஆய முறை (Coordinate system) அல்லது ஆள்கூற்று முறைமை என்பது பகுமுறை வடிவவியலில் ஓர் பகுப்பாய்வு முறைமையாகும். இம்முறையில் யூக்ளிடிய வடிவவியல் போன்ற பன்மடிவெளியில் அமைந்துள்ள புள்ளி மற்றும் பிற வடிவவியல் பொருள்களின் நிலைகள், ஒன்று அல்லது அதற்குமேற்பட்ட எண்கள் அல்லது ஆயங்களைக் கொண்டு குறிக்கப்படுகின்றன.[1][2] இவ்வாறு கணிக்கப்படும் ஆயங்களின் வரிசைமுறை மிகவும் முதன்மையானது. சில சமயங்களில் வரிசைப்படுத்தப்பட்ட ஆயங்கள் ஒவ்வொன்றும் அவை ஏற்கும் இடங்களாலும், சில சமயங்களில் x - ஆயம் , y - ஆயம் என்பது போல எழுத்துக்களாலும் குறிக்கப்படுகின்றன. ஆயங்கள் அடிப்படைக் கணிதத்தில் மெய்யெண்களாக அமைகின்றன. ஆயங்கள் சிக்கலெண்களாகவும் அமையலாம். மேலும் இவை இணைபெயர்வு வலயத்தின் நுண்ணாக்கங்களாகவும் அமைதல் உண்டு. ஆய முறையின் பயன்பாடு வடிவியல் கணக்குகளை எண்சார் கணக்குகளாக மாற்றுகிறது. அதேபோல, எண்ணியல் கணக்குகளை வடிவியல் கணக்குகளாகவும் மாற்றலாம்; பகுமுறை வடிவியலின் அடிப்படையே இது தான். [3]
ஆய முறையில் கார்ட்டீசிய ஆய முறை மற்றும் வட்ட ஆய முறை என்ற இருவகைகளும் பரவலான பயன்பாட்டில் உள்ளன. புவி மேற்பரப்பில் வரையப்படுகின்ற கற்பனைக் கோடுகளான நிலநிரைக்கோடு அல்லது நெடுவரை அல்லது நெட்டாங்கு, நிலநேர்க்கோடு அல்லது கிடைவரை அல்லது அகலாங்கு ஆகிய இரண்டும் புவிக்கோள அல்லது நிலக்கோள ஆய முறையில் பயன்படுகின்றன.
நேர்க்கோட்டு ஆய முறைகள்[தொகு]
ஆய முறைமையின் ஒரு எளிய எடுத்துக்காட்டு நேர்க்கோட்டு ஆயமுறை ஆகும். நேர்க் கோட்டின் மீதமையும் ஒவ்வொரு புள்ளியும் ஒரு மெய்யெண்ணால் குறிக்கப்படுகிறது.
இம்முறைமையில் மாறத்தக்க ஏதாவதொரு புள்ளி Oயாக (தோற்றப் புள்ளியாக) தரப்பட்டக்கோட்டின் மீது தேர்ந்தெடுக்கப்படுகிறது. இதில் இருந்து நேர்க்கோட்டின் மீதுள்ள வேறொரு புள்ளி P இன் ஆயம், புள்ளிகள் O , P இரண்டிற்கும் இடையிலுள்ள திசையுள்ள தொலைவால் வரையறுக்கப்படுகிறது. திசையுள்ள தொலைவு ஆரம் எனப்படும். ஆரம் என்பது அப்புள்ளி தோற்றப் புள்ளிக்கு எந்தப்பக்கம் அமைகிறது என்பதைப் பொறுத்தது. இடப்புறம் அமைந்தால் ஆரம் எதிர்க்குறியுடனும் வலப்பக்கம் அமைந்தால் ஆரம் நேர்க்குறியுடனும் தரப்படுகிறது. நேர்க்கோட்டின் மீதமையும் ஒவ்வொரு புள்ளிக்கும் ஒரு தனித்த மெய்யெண் ஆயம் உண்டு. அதேபோல ஒவ்வொரு மெய்யெண்ணுக்கும் அதனை ஆயமாகக் கொண்ட ஒரு தனித்த புள்ளி நேர்க்கோட்டின் மீது உண்டு.[4].[5]
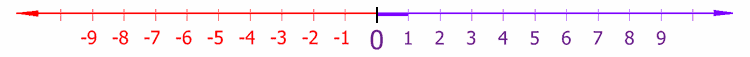
கார்ட்டீசிய ஆய முறைகள்[தொகு]

ஆய முறையின் முன்வடிவத்துக்கான சிறந்த எடுத்துக்காட்டு கார்ட்டீசிய ஆய முறையாகும். ஒரு தளத்தில் இரு செங்குத்துக் கோடுகளை தேர்ந்தெடுத்து, ஒரு இருப்புப் புள்ளியின் ஆயங்களாக கோடுகளில் இருந்து அமையும் குறியமைந்த தொலைவுகளாகும். இது ஒரு தளத்தில் உள்ள ஒவ்வொரு புள்ளியையும் துல்லியமாய்க் குழப்பம் ஏதும் இன்றிக் குறிக்கப் பயன்படும் ஒரு முறை.

முப்பருமானத்தில், மூன்று செங்குத்துத் தளங்கள் தேர்ந்தெடுக்கப்படுகின்றன. இதில் அமையும் ஓர் இருப்புப் புள்ளியைன் ஆயங்கள் அந்தத் தளங்களில் இருந்து அமையும் குறியிட்ட தொலைவுகள் ஆயங்களாக அமைகின்றன.[6] பல பருமான அல்லது n பருமான யூக்கிளிடிய வெளியில் அமையும் ஓர் இருப்புப் புள்ளியின் ஆயங்கள் n குறியிட்ட தொலைவுகளால் குறிக்கப்படும்.
திசையையும் ஆயங்களின் அச்சுகளின் வரிசைமுறையையும் பொறுத்து இது வலஞ்சுழி அமைப்பாகவோ இடஞ்சுழி அமைப்பாகவோ அமையலாம். பலவகை ஆய முறைகளில் இதுவும் ஒன்றாகும்.
வட்ட ஆய முறைகள்[தொகு]

மற்றொரு தள ஆய முறை முனைய அல்லது வட்ட ஆய முறையாகும்.[7] வட்ட ஆய முறை என்பது ஒரு சமதளத்தில் அமைந்துள்ள எப்புள்ளியையும் முறையாகக் குறிப்பிடும் ஒரு முறைமை ஆகும். இம்முறையில் சமதளத்தில் உள்ள எந்தவொரு புள்ளியும் ஒரு ஆரம், ஒரு கோணம் ஆகிய இரண்டு ஆயங்களால் குறிக்கப்பெறுகின்றது.இதில் ஓர் இருப்புப் புள்ளி முனை என வழங்குகிறது. இதில் இருந்து தோற்றத்தினை இணைக்கும் கதிர் அல்லது கோடு முனைய அச்சு எனப்படுகிறது. தரப்பட்டுள்ள θ கோணத்துக்கு முனை வழியாக ஒரே கோடு மட்டுமே அமையும். Θ கோணம் அச்சில் இருந்து கோடு வரை இடஞ்சுழி முறையில் அளக்கப்படுகிறது. இந்தக் கோட்டில் தோற்றத்தில் இருந்து r குறியிட்ட தொலைவில் ஒரே புள்ளி மட்டுமே அமையும்r. குறிப்பிட்ட இணை ஆயங்களுக்கு (r, θ) ஒரு தனிப் புள்ளி அமையும். அன்னல் ஒவ்வொரு புள்லியும் பல இணை ஆயங்களால் குறிப்பிடப்படிகிறது. எடுத்த்காட்டாக, (r, θ), (r, θ+2π), (−r, θ+π) ஆகிய அனைத்துமே ஒரே புள்ளிக்கான இணை முனையவகை ஆயங்கள் ஆகும். தரப்பட்ட θ மதிப்புக்கு, முனை (0, θ) ஆல் குறிக்கப்படும்.
கோள ஆய முறைகள்[தொகு]

கணிதவியலில் கோள ஆய முறை (spherical coordinate system) என்பது முப்பருமான வெளிக்கான ஆய முறையாகும். இதில் உள்ள இருப்புப் புள்ளிகள் மூன்று எண்களால் குறிக்கப்படும். அவை தோற்றத்தில் இருந்து அப்புள்ளிக்குள்ள ஆரத் தொலைவு, அதன் முனையக் கோணம், கிடைக்கோணம் என்பனவாகும். முனையக் கோணம் அல்லது ஏற்றக்கோணம் என்பது நிலையான தோற்றத்தின் ஊடே செல்லும் அடித் திசையில் இருந்து அளக்கப்படுகிறது. கிடைக்கோணம் அல்லது திசைக்கோணம் என்பது முனையக் கோணத்துக்குச் செங்குத்தாகவும் தோற்றத்தின் ஊடாகச் செல்லும் நிலையான தளத்தில் உள்ள அதன் வீழல் கோனமாகும். இது அந்த்த் தளத்தில் அமைந்த நிலையான மேற்கோள் திசையில் இருந்து அளக்கப்படுகிறது. இது முனைய ஆய முறையின் முப்பருமான வகையாகும்.
ஆரத் தொலைவு ஆரம் அல்லது ஆர ஆயம் எனப்படுகிறது. முனையக் கோணம், உச்சிக் கோணம் அல்லது செங்கோணம் அல்லது சரிவுக்கோணம் அல்லது இணையகலாங்கு என வழங்கப்படுகிறது.
ஆயவரிசைகளும் அவற்றின் குறியீடுகளும் நூலுக்கு நூல் மாறுபடுவதால் மிகக் கவனமாக எவ்வகையில் ஆயங்கள் அமைந்துள்ளன என்பதை அறிதல் வேண்டும். இயற்பியலில் அடிக்கடி பயன்படும் ஒரு முறையில் (r, θ, φ) ஆகியன, ஆரத்த் தொலைவையும் முனையக்கோணத்தையும் கிடக்கோணத்தையும் குறிக்க, கணிதவியலில் பயன்படும் மற்றொரு முறையில் (r, θ, φ) ஆரத் தொலைவையும் முனையக்கோணத்தையும் கிடைக்கோணத்தையும் குறிக்கிறது.இரு முறைகளிலுமே ρ is often used instead of r குறியீட்டுக்குப் பதிலாக ρ எனும் குறியீடு அடிக்கடி பயன்படுகிறது.
உருளை ஆய முறைகள்[தொகு]

உருளை ஆய முறை (cylindrical coordinate system) என்பது ஒரு முப்பருமான ஆய முறையாகும் இது இருப்புப் புள்ளியைத் தேர்ந்தெடுத்த மேற்கோள் அச்சில் இருந்துள்ள தொலைவாலும் தேர்ந்தெடுத்த மேற்கோள் திசையில் இருந்து அச்சுக்குள்ள சார்புத் திசையாலும், அச்சுக்குச் செங்குத்தாக தேர்ந்தெடுத்த மேற்கோள் தளத்தில் இருந்தமையும் தொலைவாலும் குறிக்கிறது. இருப்புப் புள்ளி மேற்கோள் தளத்துக்கு எந்தபக்கம் உள்ளது என்பதைப் பொறுத்து பின் குறிப்பிட்ட தொலைவு நேர் அல்லது எதிர்க் குறியைப் பெறும்.
அனைத்து ஆயங்களும் சுழியாக உள்ள இருப்பு தோற்றமாக அமையும். இது அச்சும் மேற்கோள் தளமும் வெட்டிக்கொள்ளும் பகுதியாகும்.
இம்முறையின் அச்சு, முனய அச்சில் இருந்து வேறுபடுத்த, உருளை அச்சு அல்லது நெடுக்கு அச்சு எனப்படுகிறது. இது தோற்றத்தில் இருந்து தொடங்கி, மேற்கோள் தளத்தில் அமைந்தவண்னம் மேற்கோள் திசையில் செல்லுகிறது.
ஒருபடித்தான ஆய முறை[தொகு]
ஒருபடித்தான ஆயங்களில் ஓர் இருப்புப் புள்ளி மும்மை எண்களால் (x, y, z) குறிக்கப்படுகின்றன. இங்கு x/z , y/z ஆகியவை அப்புள்ளியின் கார்ட்டீசிய ஆயங்கள் ஆகும்.[8] தளப்புள்ளியைக் குற்ப்பிட இரு புள்லிகளே போதும் என்றாலும் இம்முறை ஒரு கூடுதலான ஆயத்தை அறிமுகப்படுத்துகிறது. ஆனால், இம்முறை ஈறிலியைப் பயன்படுத்தாமலே வீழல் தளத்தில் எந்தவொரு புள்ளியையும் குறிப்பிடுவதால் மிகவும் பயன்மிக்கதாக அமைகிறது. பொதுவாக, இம்முறையில் ஆயங்களின் விகிதங்கள் தாம் ஆயங்களின் உண்மை மதிப்புகளை விட முதன்மையானவையாக அமைகின்றன.
வழக்கில் உள்ள பிற ஆய முறைகள்[தொகு]
வழக்கில் பின்வரும் ஆய முறைகளும் அமைகின்றன:
- வளைகோட்டு ஆயங்கள்: இந்த ஆய முறை வளைவுகள் இடைவெட்டும்போது உருவாகிறது. இது ஆய முறைகளின் பொதுமையாக்கமாக்க் கருதப்படுகிறது.
- செஞ்சரிவு ஆயங்கள்: [[ஆய மேற்பரப்புகள் செங்கோணங்களில் சந்திக்கின்றன.
- சரிவுநிலை ஆயங்கள்: இம்முறையில், ஆயப் பரப்புகள் செங்கோணத்தில் வெட்டிக் கொள்வதில்லை.
- மடக்கை-முனைய ஆய முறை ஓர் இருப்புப் புள்ளியைக் குறிக்க, தொடக்கத்தில் இருந்து புள்ளிவரை உள்ள மடக்கை தொலைவையும் தோற்றத்தை வெட்டும் மேற்கோள் கோட்டில் இருந்து அளக்கப்படும் கோணத்தையும் பயன்படுத்துகிறது.
- புளூக்கர் ஆயங்கள் முப்பருமான யூக்கிளிடிய வெளியில் ஒருபடித்தான ஆயங்களைப் பின்பற்ரி நேர்க்கோடுகளைக் குறிப்பிடப் பயன்படுகின்றன. இதற்கு ஆறு தொகுதி எண்கள் பயன்படுத்தப்படுகின்றன.
- பொதுமையாக்க ஆயங்கள் இலாகுரேஞ்சியமுறையில் இயக்கவியலை ஆய்வுசெய்ய பயன்படுகின்றன.
- வரன்முறை ஆயங்கள் ஆமில்டன் முறையில் இயக்கவியலை ஆய்வுசெய்ய பயன்படுகின்றன.
- பருமைய ஆயங்கள் மும்மை வரைவுகளில், குறிப்பாக முக்கோணங்களின் பகுப்பாய்வில் பயன்படுகின்றன.
- முக்கோட்டு ஆயங்கள் முக்கோணச் சூழலில் பயன்படுகின்றன.
ஆயங்களைப் பயன்படுத்தாமலே வளைவை இயல்பான சமன்பாடுகளால் விவரிக்கும் முறைகளும் உள்ளன. இவை மாறாத அளவுகளாகிய வளைமை, வட்டவில் நீளம் ஆகியவற்றைப் பயன்படுத்துகின்றன. பின்வரும் சமன்பாடுகள் இவ்வகைமையில் அடங்கும்.
- வேவல் சமன்பாடு வட்டவில் நீளத்தையும் தொடுகோட்டுக் கோணங்களையும் உறவுபடுத்துகிறது.
- செசாரோ சமன்பாடு வளைமையையும் வட்டவில் நீளத்தையும் சார்பு படுத்துகிறது.
சார்பியல் ஆய முறைகள்[தொகு]
- எடிங்டன்–பிங்கல்சுட்டீன் ஆயங்கள்
- காசிய முனைய ஆயங்கள்
- குல்சுடிராண்டு–பைன்லெவே ஆயங்கள்
- செஞ்சரிவு ஆயங்கள்
- குரூசுகால்–சுசேகெரெசு ஆயங்கள்
- சுவார்சுசைல்டு ஆயங்கள்
மேலும் பார்க்க[தொகு]
- கார்ட்டீசிய ஆய முறை
- வட்ட ஆய முறை
- கோள ஆய முறை
- உருளை ஆய முறை
- பகுமுறை வடிவவியல்
- விண்கோள ஆய முறைகள்
- பகவுநிலை ஆயங்கள்
- மேற்கோள் சட்டகம்
- கலீலிய உருமாற்றம்
- புவிக்கோள ஆய முறை
மேற்கோள்கள்[தொகு]
- ↑ Woods p. 1
- ↑ Weisstein, Eric W., "Coordinate System", MathWorld.(ஆங்கில மொழியில்)
- ↑ Weisstein, Eric W., "Coordinates", MathWorld.
- ↑ Woods p. 8
- ↑ James Stewart (mathematician); Redlin, Lothar; Watson, Saleem (2008). College Algebra (5th ). Brooks Cole. பக். 13–19. பன்னாட்டுத் தரப்புத்தக எண்:0-495-56521-0.
- ↑ "Rectangular Coordinates (x, y, z)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd, 3rd print ). New York: Springer-Verlag. 1988. பக். 9–11 (Table 1.01). பன்னாட்டுத் தரப்புத்தக எண்:978-0-387-18430-2.
- ↑ Finney, Ross; George Thomas; Franklin Demana; Bert Waits (June 1994). Calculus: Graphical, Numerical, Algebraic (Single Variable Version ). Addison-Wesley Publishing Co.. பன்னாட்டுத் தரப்புத்தக எண்:0-201-55478-X.
- ↑ Jones, Alfred Clement (1912). An Introduction to Algebraical Geometry. Clarendon.
வெளி இணைப்புகள்[தொகு]
உசாத்துணைகள்[தொகு]
- Voitsekhovskii, M.I.; Ivanov, A.B. (2001), "Coordinates", in Hazewinkel, Michiel (ed.), Encyclopedia of Mathematics, Springer, ISBN 978-1556080104
- Woods, Frederick S. (1922). Higher Geometry. Ginn and Co.. பக். 1ff. https://books.google.com/books?id=3ZULAAAAYAAJ&pg=PA1#v=onepage&q&f=false.
- Shigeyuki Morita; Teruko Nagase; Katsumi Nomizu (2001). Geometry of Differential Forms. AMS Bookstore. பக். 12. பன்னாட்டுத் தரப்புத்தக எண்:0-8218-1045-6. https://books.google.com/books?id=5N33Of2RzjsC&pg=PA12.

