நம்பக இடைவெளி
இக்கட்டுரை கூகுள் மொழிபெயர்ப்புக் கருவி மூலம் உருவாக்கப்பட்டது. இதனை உரை திருத்த உதவுங்கள். இக்கருவி மூலம்
கட்டுரை உருவாக்கும் திட்டம் தற்போது நிறுத்தப்பட்டுவிட்டது. இதனைப் பயன்படுத்தி இனி உருவாக்கப்படும் புதுக்கட்டுரைகளும் உள்ளடக்கங்களும் உடனடியாக நீக்கப்படும் |
புள்ளியியலில் நம்பக இடைவெளி (சிஐ ) என்பது ஒருவகைப்பட்ட இன அளவுருவின் இடைவெளி மதிப்பீடாகும். அளவுருவை ஒரு ஒற்றை மதிப்பைக் கொண்டு அளவிடுவதற்கு பதிலாக கொடுக்கப்பட்ட அளவுருவை இடைவெளி சேர்த்துக்கொள்கிறது. எனவே, நம்பக இடைவெளிகள் மதிப்பீட்டின் நம்பகத்தன்மையை குறிப்பிடுவதற்கு பயன்படுத்தப்படுகின்றன. எந்த அளவிற்கு இந்த இடைவெளி அளவுருவை உள்ளிட்டிருக்கிறது என்றால் இது நம்பக அளவு அல்லது நம்பக குணகத்தினால் தீர்மானிக்கப்படுகிறது. விரும்பிய நம்பக அளவை அதிகரிப்பது நம்பக இடைவெளியை அகலப்படுத்தும்.
நம்பக இடைவெளி எப்போதும் ஒரு குறிப்பிட்ட நம்பக அளவால் தகுதிபெறச் செய்யப்படுகிறது, வழக்கமாக சதவிகிதத்தில் வெளிப்படுத்தப்படுகிறது; எனவே ஒருவர் "95 சதவிகித நம்பக அளவு" என்று கூறலாம். நம்பக இடைவெளியின் முடிவுப் புள்ளிகள் நம்பக வரம்புகள் என்று குறிப்பிடப்படுகின்றன. கொடுக்கப்பட்ட சூழ்நிலையிலான கொடுக்கப்பட்ட மதிப்பீட்டிற்கு அதிகப்படியான நம்பக அளவு நம்பக இடைவெளியை அகலப்படுத்தச்செய்வதாக இருக்கும்.
நம்பக இடைவெளியின் கணக்கீடு பொதுவாக மதிப்பீட்டு நிகழ்முறையின் இயல்பிற்கு அனுமானங்கள் தேவைப்படுகின்றன - இது பிரதானமாக ஒரு அளவுரு முறையாகும் - உதாரணத்திற்கு, மாதிரியிலிருந்து வந்துள்ள இனப் பகிர்மானம் இயல்பானதாக இருக்கிறது என்ற அனுமானத்தைப் பொறுத்திருக்கிறது. இதனால், கீழே விவாதிக்கப்படும் நம்பக இடைவெளிகள் தன்முனைப்பான புள்ளிவிவரங்கள் அல்ல, இருப்பினும் தன்முனைப்பிற்கான மேம்படுத்தல்களை உருவாக்க முடியும் - பார்க்க தன்முனைப்பு நம்பக இடைவெளிகள்.
நம்பக இடைவெளிகள் நேமன்-பியர்ஸன் (பொதுநிலைவாத) புள்ளிவிவரங்களுக்குள்ளாக பயன்படுத்தப்படுகின்றன; பேஸியன் புள்ளிவிவரத்தில் இதேபோன்ற ஒரு பாத்திரம் நம்பகமான இடைவெளியால் நிகழ்த்தப்படுகிறது, ஆனால் நம்பகமான இடைவெளி மற்றும் நம்பக இடைவெளி வேறுபட்ட கருத்தாக்க அடித்தளங்களைக் கொண்டிருக்கின்றன என்பதோடு பொதுவாக அவை வேறுபட்ட மதிப்புக்களையே எடுத்துக்கொள்கின்றன. பொதுநிலைவாதத்திற்கும் பேஸியன் புள்ளிவிவரங்களுக்கும் இடையிலுள்ள பொதுவான விவாதத்தின் ஒரு பகுதியாக இந்த புள்ளிவிவரங்களில் உள்ள உடன்பாடின்மை மிகவும் பயன்மிக்கது என்பதோடு பொருத்தமானதுமாகும், மாற்றுக்கள் மற்றும் விமர்சனங்களில் விவாதிக்கப்பட்டுள்ளதுபோல்.
கருத்தாக்க அடிப்படை[தொகு]

இடைவெளி மதிப்பீடுகள் மைய மதிப்பீடுகளோடு முரண்படக்கூடும். ஒரு மைய மதிப்பீடு என்பது ஆர்வம் காட்டப்படுகின்ற இன அளவுருவின் மதிப்பீடாக கொடுக்கப்பட்ட ஒரு ஒற்றை மதிப்பீடாகும். ஒரு இடைவெளி மதிப்பீடானது அளவுரு இருக்கவேண்டிய இடமாக மதிப்பிடப்பட்ட இடத்திற்குள்ளாக அதற்கு மாற்றாக குறிப்பிடப்படுகிறது. நம்பக இடைவெளிகள் மதிப்பீடுகளின் நம்பகத்தன்மையைக் காட்டுவதற்கு பொதுவாக அட்டவணைகள் அல்லது வரைபடங்கள் அதே அளவுருக்களின் மைய மதிப்பீடுகளோடு குறிப்பிடப்படுகிறது.
உதாரணத்திற்கு, ஒரு நம்பக இடைவெளி கணக்கெடுப்பு முடிவுகள் எவ்வளவு நம்பகமானவை என்பதை விளக்குவதற்கு பயன்படுத்தப்படலாம். தேர்த்ல் வாக்களிப்பில் முடிவானது, ஒரு குறிப்பிட்ட கட்சிக்கு வாக்களிக்கவிருக்கும் 40 சதவிகிதத்தினராக இருக்கலாம். மொத்த இனத்திலும் சரிவிகிதத்திற்கான 90 சதவிகித நம்பிக்கை இடைவெளியானது அந்த கணக்கெடுப்பு நாளில் அதே நோக்கத்தைக் கொண்டிருப்பது 38 முதல் 42 சதவிகிதமாக இருக்கலாம். இதே தரவிலிருந்து ஒருவர் இந்த நிகழ்வில் 34 முதல் 44 சதவிகிதம் வரை இருக்கக்கூடிய 95 சதவிகித நம்பக இடைவெளியைக் கணக்கிடலாம். கொடுக்கப்பட்ட நம்பக அளவு மற்றும் பிற எல்லாமும் சமமானதாக இருக்கின்றவிடத்தில் சிறிய சிஐ உடனான முடிவு பெரிய சிஐ உடனான முடிவைக் காட்டிலும் மிகவும் நம்பத்தகுந்ததாக இருக்கும். நம்பக இடைவெளியின் அகலத்தை தீர்மானிக்கும் ஒரு முக்கியமான காரணி மதிப்பீட்டு நடவடிக்கையில் பயன்படுத்தப்பட்ட மாதிரியின் அளவாகும், உதாரணத்திற்கு இந்த கணக்கெடுப்பில் பங்கேற்பவர்களின் எண்ணிக்கை.
நம்பக இடைவெளிகள் புள்ளிவிவர சிறப்பு சோதித்தலோடு நெருக்கமான உறவு கொண்டிருக்கின்றன. பல சூழ்நிலைகளிலும், அளவுருவின் மைய மதிப்பீடு நம்பக அளவு P இல் நம்பக இடைவெளி [a ,b ] உடன் X என்றால் இடைவெளிக்கு வெளியிலான எந்த இடைவெளியும் [a ,b ] நம்பக இடைவெளியை உருவாக்குவதற்கென்று செய்யப்பட்ட அதே பகிர்மான அனுமானங்களின் கீழ் சிறப்பு அளவு α = 1 − P இல் X இல் இருந்து குறிப்பிடத்தகுந்த அளவிற்கு வேறுபட்டிருக்கும். அதாவது, இரண்டாவது அளவுருவின் மதிப்பீட்டில் a க்கு குறைவான அல்லது b க்கு அதிகமான மதிப்பை நாம் காண்கிறோம், α சிறப்பு அளவில் இந்த அளவுருவின் மதிப்பீடு X க்கு சமமான நிக மதிப்பாக இருக்கும் பூஜ்ஜிய கருதுகோளை நாம் நிராகரிக்கிறோம்; மாற்றாக, இரண்டாவது அளவுருவின் மதிப்பீடு இடைவெளிக்கு [a ,b ] உள்ளாக இருந்தால் அளவுரு X ஐ சமமானதாக்குகின்ற பூஜ்ஜிய கருதுகோளை நம்மால் நிராகரிக்க முடியாது. இதன் தொடர்ச்சியாக, இரண்டு அளவுருக்களின் மதி்ப்பீடுகள் (உதாரணத்திற்கு, இரண்டு தனிப்பட்ட பொருள் குழுக்களின் மதிப்பிலான மாறுபாட்டின் இடைநிலை மதிப்புக்கள்) மேல்கவியாத கொடுக்கப்பட்ட P மதிப்பில் நம்பக இடைவெளிகளைக் கொண்டிருக்கும், இரண்டு மதிப்புக்கள் α இன் தொடர்புடைய மதிப்பில் குறிப்பிடத்தகுந்த அளவிற்கு மாறுபட அதிக சாத்தியமுள்ளது. இருப்பினும், இது இரண்டு சராசரிகளுக்கு இடையிலான வேறுபாட்டின் சிறப்பம்சத்தினுடைய சோதனை அந்த வேறுபாட்டின் மாதிரியாக்க பகிர்மானத்தைச் சார்ந்திருக்கிறது என்பதால் இது முற்றிலும் உண்மையல்ல, அதேசமயத்தில் நம்பக இடைவெளிகள் இரண்டு முழு மதிப்புக்களின் மாதிரியாக்க பகிர்மானத்திற்கு தொடர்புடையவை அல்ல.[1][2]
நம்பகப் பகுதிகள் பலதரப்ட்ட அளவுகளைக் கையாள நம்பக இடைவெளியை பொதுமைப்படுத்துகிறது. இதுபோன்ற பகுதிகள் சாத்தியமுள்ள மதிப்பீட்டுப் பிழைகளை மட்டும் நீட்டிக்கச்செய்வதில்லை, ஆனால் இது ஒரு அளவு நம்பத்தகுந்ததாக இல்லாமல், மற்றொன்றும் நம்பத்தகுந்ததாக இல்லாமல் இருந்தால் இது ஒரு பிரச்சினையாகுமா (உதாரணத்திற்கு) என்பதையும் வெளிக்காட்டுகிறது. மேலும் பார்க்க நம்பகப் பட்டைகள்.
பயன்பாட்டு நடைமுறையில், நம்பக இடைவெளிகள் வகைமாதிரியாக 95 சதவிகித நம்பக அளவில் குறிப்பிடப்படுகின்றன.[3] இருப்பினும், வரைபடம் மூலம் அளிக்கப்படும்போது, நம்பக இடைவெளிகளை சில நம்பக அளவுகளில் காட்ட முடியும், உதாரணத்திற்கு 50%, 95% மற்றும் 99%.
புள்ளிவிவர கோட்பாடு[தொகு]
வரையறை[தொகு]
தற்போக்கு இடைவெளிகளாக உள்ள நம்பக இடைவெளிகள்[தொகு]
கொடுக்கப்பட்ட தரவுத்தொகுதியின் அடிப்படையில் நம்பக இடைவெளிகள் கட்டமைக்கப்படுகின்றன: x தரவுத்தொகுதியில் உள்ள கண்டுபிடிப்புகளின் தொகுதியைக் குறிப்பிடுகிறது, அத்துடன் X = x என்று கண்டுபிடிக்கப்பட்ட முடிவைக் கொண்டிருக்கும் தற்போக்கு மாறுபாட்டாக X கருதப்படுமிடத்தில் அதே இனத்திலிருந்து முடிவுகள் கண்டுபிடிக்கப்பட்டிருக்கலாம் என்று கருதும்போது X பயன்படுத்தப்படுகிறது. நம்பக இடைவெளியானது u (.) மற்றும் v (.) என்ற செயல்பாட்டு இணைகளின் மூலம் குறிப்பிடப்படுகிறது, கொடுக்கப்பட்ட தரவுத் தொகுதிக்கான நம்பக இடைவெளி (u (x ), v (x )) இடைவெளியாக வரையறுக்கப்பட்டிருக்கிறது. நம்பக இடைவெளியின் வரையறையை முழுமைப்படுத்துவதற்கு, சிஐ உள்ளார்ந்த மதிப்பீட்டை வழங்குவதற்கான அளவைப் புரிந்துகொள்ள வேண்டியிருக்கிறது. ஒருவேளை இந்த அளவு w என்று இருக்கிறது. w க்கான நம்பக இடைவெளி என்னவாக இருக்கும் என்பதற்கு நெருக்கமான (u (x ), v (x )) இடைவெளியை உருவாக்கும் u (.) மற்றும் v (.) விதிகளின் உடைமைப்பொருள் (u (X ), v (X )) என்று வழங்கப்பட்டிருக்கும் தற்போக்கு இடைவெளிகளின் தொகுப்பின் உடைமைப்பொருள்களுக்கு தொடர்புடையதாக இருக்கிறது: அதாவது தற்போக்கு மாறுபாடுகளாக முடிவுப் புள்ளிகளை கருதுதல். இந்த உடைமைப்பொருள் உள்ளடக்கு நிகழ்தகவாக இருக்கிறது அல்லது w ஐ உள்ளிட்டிருக்கும் தற்போக்கு இடைவெளி c நிகழ்தகவு,
இங்கே முடிவுப்புள்ளிகளான U = u (X ) மற்றும் V = v (X ) ஆகியவை தரவுத்தொகுதியில் உள்ள மதிப்புக்களிலிருந்து பெறப்படும் புள்ளிவிவரங்களாகும் (அதாவது, கண்டுபிடிக்கக்கூடிய தற்போக்கு மாறுபாடு). தற்போக்கு இடைவெளியானது (U , V ).
அனுமானத்திற்கான நம்பக இடைவெளி[தொகு]
மேலை குறிப்பிடப்பட்டவற்றிற்கு புள்ளிவிவர அனுமானத்திற்கான நீடிக்கவல்ல சராசரிகளை வழங்குவதற்கு மேற்கொண்டு ஏதோ ஒன்று தேவைப்படுகிறது: மதிப்பிடப்பட்ட அளவு மற்றும் முடிவு X இன் நிகழ்தகவு பகிர்மானத்திற்கு இடையிலுள்ள இணைப்பு மதிப்பிடப்படவேண்டிய அளவான கண்டுபிடிக்கப்பட முடியாத அளவுரு θ மற்றும் உடனடி ஆர்வமுள்ளதாக இல்லாத பிற கண்டுபிடிக்கப்பட முடியாத அளவுருக்கள் φ ஆலும் இந்த நிகழ்தகவு பகிர்மானம் விளக்கப்பட வேண்டிவரலாம் . உடனடி ஆர்வம் காட்டப்படாத இந்த பிற அளவுகள் φ என்பது தொந்தரவு அளவுருக்கள் எனப்படுகின்றன, இவற்றைக் கையாளுவதற்கு புள்ளிவிவர கோட்பாடு சில வழியைக் கண்டுபிடிக்க வேண்டியிருக்கிறது.
0 மற்றும் 1க்கு இடையிலான எந்த αக்கும் இடையிலான θக்கான நம்பக இடைவெளியின் வரையறை பின்வரும் இடைவெளி
எதற்கானதென்றால்
மற்றும் u (X ) மற்றும் v (X ) ஆகியவை கண்டுபிடிக்கப்படக்கூடிய தற்போக்கு மாறுபாடுகள், அதாவது, ஒருவர் u (X ) மற்றும் v (X ) இன் மதிப்புக்களை தெரிந்துகொள்ளும் விதமாக θ , φ கண்டுபிடிக்க இயலாத அளவுகளின் மதி்ப்பை தெரிந்துகொள்ள வேண்டியதில்லை.
எண் 1 − α (சிலபோது சதவிகிதமாக குறிப்பிடப்படுவது 100%·(1 − α )) நம்பக அளவாக இருக்கிறது, சிலபோது நம்பக குணகம் என்றழைக்கப்படுகிறது. α சிறிய எண்ணாக இருக்கக்கூடியவிடத்தில் பெரும்பாலான புத்தகங்கள் இந்த உடன்பாட்டை ஏற்றுக்கொண்டிருக்கின்றன. இங்கே தற்போக்கு மாறுபாடு X ஆனது (θ , φ ) ஆல் விளக்கப்பட்ட பகிர்மானத்தைக் கொண்டிருக்கும்போது நிகழ்தகவைக் குறிப்பிடுவதற்கு Prθ ,φ பயன்படுத்தப்படுகிறது. இந்த விவரக்குறிப்பின் ஒரு முக்கியமான பாகம் என்னவெனில் தற்போக்கு இடைவெளி (U , V ) θ இன் அசல் மதிப்பு என்ன என்ற பொருட்டின்றி உயர் நிகழ்தகவுடனான அறியப்படாத மதிப்பு θ ஐ உள்ளிட்டிருக்கிறது என்பதுதான்.
இங்கே Prθ ,φ வெளிப்படையாக கொடுக்கப்பட்ட அளவுருவாக்க பகிர்மான இனத்தை குறிப்பிட வேண்டியதில்லை, இருப்பினும் அவ்வாறுதான் செய்கிறது. மாறுபாடு X , உண்மையின் அதே இனத்திலிருந்து அல்லது அதே பதிப்பிலிருந்து x இன் பிற சாத்தியமுள்ள உணர்தல்களோடு கற்பிதமாக மட்டுமே தொடர்புகொண்டிருக்கிறது என்பதால், (θ , φ ) அளவுருக்கள் X இன் பகிர்மானம் வேறுபட்ட விளக்கங்களைக் கொண்டிருக்கக்கூடிய பிற உண்மைப் பதிப்புக்களை நாம் பரிசீலிக்க வேண்டும் என்பதைக் குறிப்பிடுகிறது.
தற்போக்கு முடிவுகளுக்கான இடைவெளிகள்[தொகு]
நம்பக இடைவெளிகளை தற்போக்கு அளவுகள் மற்றும் மேலே குறிப்பிடப்பட்டதில் உள்ளபடி நிலைப்படுத்தப்பட்ட அளவுகளுக்கானவை என்று வரையறுக்கலாம் பார்க்க முன்னூகிப்பு இடைவெளி. பின்வருமாறு என்றால், இதற்காக, X புள்ளிவிவரரீதியில் சார்ந்திருக்கவோ அல்லது சார்ந்திருக்கவோ செய்யாத கூடுதலான ஒற்றை-மதிப்பீட்டு தற்போக்கு மாறுபாடு Y ஐ கவனத்தில் கொள்ளவும். பின்னர் (u (x ), v (x )) இடைவெளியைக் கட்டமைப்பதற்கான விதி இன்னும் கண்டுபிடிக்கப்பட வேண்டியதாக இருக்கின்ற Y இன் y க்கான நம்பக இடைவெளியை வழங்குகிறது
இங்கே அளவுருக்கள் (θ , φ ) ஆல் விளக்கப்படும்போது தற்போக்கு மாறுபாடுகள் (X , Y ) இன் கூட்டுப் பகிர்மானத்திற்கும் மேலான நிகழ்தகவைக் குறிப்பிட Prθ ,φ பயன்படுத்தப்படுகிறது.
தோராயமான நம்பக இடைவெளிகள்[தொகு]
தரநிலையற்ற பயன்பாடுகளுக்கு, தேவையான உடைமைப்பொருள்களைக் கொண்டிருக்கும் நம்பக இடைவெளிகளைக் கட்டமைப்பதற்கான விதிகளைக் கண்டுபிடிப்பது சிலபோது சாத்தியமில்லாததாக இருக்கிறது. ஆனால் நடைமுறையில் பயன்மிக்க இடைவெளிகளை இப்போதும் கண்டுபிடிக்க முடியும். தற்போக்கு இடைவெளிக்கான உள்ளடக்கு நிகழ்தகவு c (θ , φ ) வரையறுக்கப்படுவது
அத்துடன் இந்த இடைவெளியைக் கட்டமைப்பதற்கான விதி பின்வருமாறு இருந்தால் நம்பக இடைவெளியை அளிப்பதாக ஏற்றுக்கொள்ளப்படலாம்
தோராயமாக்கலின் ஏற்றுக்கொள்ளக்கூடிய அளவிற்கு.
பேஸியன் இடைவெளி மதிப்பீடுகள்[தொகு]
ஒரு பேஸியன் இடைவெளி மதி்ப்பீடு நம்பத்தகுந்த இடைவெளி எனப்படுகிறது. மேலே குறிப்பிடப்பட்டுள்ளபடி இதேபோன்ற குறிப்புரையை பெருமளவிற்கு பயன்படுத்தி, θ இன் அறியப்படாத உண்மை மதிப்பிற்கான நம்பத்தருந்த இடைவெளியின் வரையறை, கொடுக்கப்பட்ட α [4] க்கு,
இங்கே θ இன் அறியப்படாத மதிப்பு தற்போக்கு மாறுபாடாக பயன்படுத்தப்படுகிறது என்பதை வலியுறுத்த θ பயன்படுத்தப்படுகிறது. இடைவெளிகளின் இந்த இரண்டு வகைகளினுடைய வரையறைகள் பின்வருமாறு ஒப்பிடப்படலாம்.
- நம்பக இடைவெளியின் வரையறை கொடுக்கப்பட்ட (θ , φ )க்கு (அல்லது இந்த மதிப்புக்களிலான நிபந்தனை) X இன் பகிர்மானத்திலிருந்து நிகழ்தகவுகள் கணக்கிடப்படுவதோடு சம்பந்தப்பட்டிருக்கிறது என்பதுடன் இந்த நிபந்தனை (θ , φ ) இன் எல்லா மதிப்புக்களுக்காகவும் வைத்துக்கொள்ளப்பட வேண்டியிருக்கிறது.
- நம்பத்தகுந்த இடைவெளியின் வரையறை X = x இன் கண்டுபிடிக்கப்பட்ட மதிப்புக்களில் Θ நிபந்தனையின் பகிர்மானத்திலிருந்தும், இந்த கடைசி அளவு φ இல் உள்ள தொந்தரவு அளவுருக்கள் குறித்த நிச்சமின்மையோடு தொடர்புடைய தற்போக்கு மாறுபாடாக இருக்குமிடத்திலான Φ மதிப்புக்களுக்கும் மேற்பட்ட விளிம்பாக்கப்பட்டதிலிருந்து (அல்லது சராசரியாக்கப்பட்டதிலிருந்து) நிகழ்தகவுகள் கணக்கிடப்படுவதோடு சம்பந்தப்பட்டிருக்கிறது.
மேலே உள்ள தொந்தரவு அளவுருக்களின் கையாளுதல் நம்பக மற்றும் நம்பத்தகுந்த இடைவெளிகலை ஒப்பிடும் விவாதங்களிலிருந்து தொடர்ந்து நீக்கப்பட்டுவிடுகிறது என்பதை கவனிக்கவும், ஆனால் இது குறிப்பிடத்தகுந்த அளவிற்கு இந்த இரண்டு நிகழ்வுகளுக்கும் இடையில் வேறுபட்டிருக்கிறது.
சில எளிய தரநிலை நிகழ்வுகளில், ஒரே தரவுத் தொகுதியிலிருந்து நம்பக மற்றும் நம்பத்தகுந்த இடைவெளிகளாக உருவாக்கப்படும் இடைவெளிகள் சமமானவையாக இருக்கலாம். மிதமான அல்லது வலுவான முந்தையத் தகவல் பேஸியன் பகுப்பாய்வில் உள்ளிடப்பட்டால் அவை எப்போதும் மிகவும் வேறுபட்டதாக இருக்கும்.
விரும்பத்தகுந்த உடைமைப்பொருள்கள்[தொகு]
நிலையான புள்ளிவிவர நடைமுறைகளைப் பயன்படுத்தும்போது, நம்பக இடைவெளிகளைக் கட்டமைப்பதற்கான நிலையான வழிகள் இருந்துகொண்டிருக்கும். இவை இந்த நடைமுறை நம்பியிருப்பது உண்மை என்ற அனுமானத்தை வழங்கும் சில விரும்பத்தகுந்த உடைமைப்பொருள்களை எதிர்கொள்ளும்விதமாக இவை திட்டமிடப்படலாம். இந்த விரும்பத்தகுந்த உடைமைப்பொருள்கள் பின்வருமாறு விளக்கப்படலாம்: ஏற்றுக்கொள்ளக்கூடியது, அனுகூலமாக்கக்கூடியது மற்றும் மாறுபடாதது. இந்த "ஏற்பு" மிகவும் முக்கியமானது, இது "அனுகூலத்தால்" நெருக்கமாக பின்பற்றப்படுகிறது. "மாறுபடாதது" இடைவெளியைக் கட்டமைப்பதற்கான விதியைக் காட்டிலும் நம்பக இடைவெளியின் பெறுதல் முறையின் உடைமைப்பொருளாக கருதப்படலாம். தரநிலை அல்லாத பயன்பாடுகளில், இதே விரும்பத்தகுந்த உடைமைப்பொருள்கள் கண்டுபிடிக்கப்படலாம்.
- ஏற்பு. துல்லியமாகவோ அல்லது சிறந்த தோராயமாகவோ நம்பக இடைவெளி பின்பற்றப்பட வேண்டும் என்பதன் பெயரளவு உள்ளிடல் நிகழ்தகவு (நம்பக அளவு) கொண்டிருக்க வேண்டும் என்பதை இது குறிப்பிடுகிறது.
- அனுகூலமாக்கம். நம்பக இடைவெளியைக் கட்டமைப்பதற்கான விதி முடிந்தவரை தரவுத் தொகுதியில் உள்ள தகவலை பயன்படுத்திக்கொள்ள வேண்டும் என்பதை இது குறிக்கிறது. இந்த ஒன்றை மீண்டும் கொண்டுவருவது தரவுத்தொகுதியின் பாதியை தூக்கியெறிந்துவிடுகிறது என்பதுடன் ஏற்புடைய நம்பக இடைவெளியைப் பெறும் திறனுள்ளதாகவும் இருக்கிறது. அனுகூலமாக்கலை மதிப்பிடுவதற்கான ஒரு வழி இடைவெளியின் நீளத்தினால் ஆகும், எனவே நம்பக இடைவெளியை கட்டமைப்பதற்கான விதியானது இடைவெளிகளின் அகலங்கள் வகைமாதிரியாக சுருக்கமாக இருப்பதற்கு வழியமைக்கும் என்றால் சிறந்த முறையில் தீர்மானிக்கப்பட வேண்டும்.
- மாற்றமின்மை. பல பயன்பாடுகளிலும் மதிப்பிடப்படும் அளவு இந்தளவிற்கு இறுக்கமாக வரையறுக்கப்படாமல் போகலாம். உதாரணத்திற்கு, ஒரு கணக்கெடுப்பு ஒரு இனத்திலான நடுவூடான வருமானத்தின் மதிப்பீட்டிற்கு காரணமாக அமையலாம், ஆனால் இது நடுவூடான வருமானத்தின் மடக்கையினுடைய மதி்ப்பீட்டை வழங்குவதாக சமமான அளவிற்கு கருதப்படலாம், இது வழங்கப்படுவது வரைபட முடிவுகளை வழங்குவதற்கான பொதுவான அளவையாக இருக்கிறது. நடுவூடான வருமானத்திற்கு நம்பக இடைவெளியை கட்டமைப்பதற்கு பயன்படுத்தப்படும் முறையானது நடுவூடான வருமானத்தின் மட்கைக்கான நம்பக இடைவெளியைக் கட்டமைப்பதற்கு பயன்படுத்தப்படுகையில் சமமான முடிவுகளை வழங்குவது விரும்பத்தகுந்ததாகும்: குறிப்பாக பிந்தைய இடைவெளியின் முனைகளில் உள்ள மதிப்புக்கள் முந்தைய இடைவெளியின் முனைகளினுடைய மடக்கையாக இருக்கலாம்.
பெறுதல் முறைகள்[தொகு]
தரநிலை அல்லாத பயன்பாடுகளுக்கு, நம்பக இடைவெளிகளைக் கட்டமைப்பதற்கான விதியைப் பெறுவதற்கு எடுத்துக்கொள்ளக்கூடிய சில வழிகள் இருக்கின்றன. தரநிலைப்படுத்தப்பட்ட நடைமுறைகளுக்கான நிறுவப்பட்ட விதிகள் உண்மையென்று நிரூபிக்கப்பட வேண்டும் அல்லது இந்த வழிகள் சிலவற்றின் வழியாக விளக்கப்பட வேண்டும். வகைமாதிரியாக நம்பக இடைவெளிகளைக் கட்டமைப்பதற்கான விதியானது பரிசீலி்க்கப்படும் அளவின் மைய மதிப்பீட்டைக் கண்டுபிடிக்கும் குறிப்பிட்ட வழியோடு நெருக்கமாக இணைக்கப்பட வேண்டும.
- புள்ளிவிவரங்கள்
- இது மதிப்பீட்டிற்கான கணங்கள் முறைக்கு நெருக்கமான தொடர்புகொண்டிருக்கிறது. மதிப்பிடப்படும் அளவு சராசரியாக இருக்குமிடத்தில் ஒரு உதாரணம் தோன்றுகிறது, இந்த நிகழ்வில் இயல்பான மதிப்பீடு மாதிரி சராசரியாக இருக்கிறது. வழக்கமான வாதங்கள் மாதிரி மாறுபாடு மாதிரி சராசரியின் மாறுபாட்டைக் கணக்கிடுவதற்கு பயன்படுத்தப்படலாம். நிஜ சராசரிக்கான ஒரு எளிய நம்பக இடைவெளி கட்டமைக்கப்படுவது மாதிரி மாறுபாட்டின் இருமடி மூலத்தின் பெருக்கமாக இருக்கும் அகலத்தோடு மாதிரி சராசரியில் மையப்படுத்தப்படுகிறது.
- சாத்தியப்பாட்டு கோட்பாடு
- அதிகபட்ச சாத்தியக் கொள்கையைப் பயன்படுத்தி மதிப்பீடுகள் கணக்கிடப்படுமிடத்தில், இதற்கான கோட்பாடு மதிப்பீடுகளுக்கான நம்பக இடைவெளிகள் அல்லது நம்பகப் பிரதேசங்களைக் கட்டமைக்கும் இரண்டு வழிகளை வழங்குகிறது.
- சமன்பாடுகளை மதிப்பிடுதல்
- இங்குள்ள மதிப்பீட்டு அணுகுமுறை தருணங்களின் முறையை பொதுமைப்படுத்துதல் மற்றும் அதிகபட்ச சாத்தியப்பாட்டு அணுகுமுறையை பொதுமைப்படுத்துதல் ஆகிய இரண்டையும் பரிசீலிக்கலாம். மதிப்பிடுதல் சமன்பாடுகளிலிருந்து பெறப்பட்டட மதிப்பீடுகளின் அடிப்படையில் கட்டமைப்பதற்கான நம்பக இடைவெளிகளை அனுமதிக்கும் அதிகபட்ச சாத்தியப்பாட்டு கோட்பாட்டின் முடிவுகளின் சம்பந்தப்பட்ட பொதுமைப்படுத்தல்கள் இருக்கின்றன.
- வழியாக சிறப்பு சோதனை
- சிறப்பு சோதனைகள் அளவுருக்களின் பொது மதிப்பீடுகளுக்கு இருக்கின்றன என்றால் பின்னர் நம்பக இடைவெளிகள்/பிரதேசங்கள், (1-p) இன் சிறப்பு அளவில் நிராகரிக்கப்படாத கொடுக்கப்பட்ட மதிப்பாக உள்ள நிஜ மதிப்பு பூஜ்ஜிய கருதுகோள் சிறப்பு சோதனைக்கான எல்லா விஷயங்களும் 100p% நம்பகப் பிரதேசத்தில் உள்ளிடப்படுவதன் மூலம் கட்டமைக்கப்படுகின்றன.
எடுத்துக்காட்டுகள்[தொகு]
நடைமுறை உதாரணம்[தொகு]
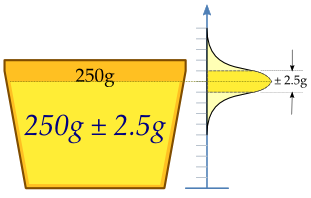
ஒரு இயந்திரம் வெண்ணெயை கோப்பைகளில் நிரப்புகிறது, கோப்பையின் கொள்ளளவு 250 மில்லிகிராம் வெண்ணெயாக இருக்க சரிசெய்யப்படக்கூடியதாக இருக்கிறது. இயந்திரமானது எல்லாக் கோப்பைகளையும் துல்லியமாக 250 கிராம்கள் நிரப்ப முடியாது என்றால் கோப்பையின் கொள்ளளவு சில மாறுபாட்டைக் காட்டும், அத்துடன் இது தற்போக்கு மாறுபாடு X என்று கருதப்படும். இந்த மாறுபாடு 2.5 கிராம் என்ற நியமச்சாய்வோடு ஏறத்தாழ 250 கிராம் சராசரி என்ற விரும்பிய இயல்பான பகி்ர்மானமாக இருப்பதாக யூகிக்கப்படுகிறது. இந்த இயந்திரம் போதுமான அளவிற்கு சரிசெய்துகொள்ளக்கூடியதா என்பதைத் தீர்மானிப்பதற்கு, n = 25 கோப்பைகள் விளிம்பின் மாதிரி தற்போக்காக தேர்ந்தெடுக்கப்பட்டு கோப்பைகள் எடையிடப்படும். வெண்ணெயின் எடைகள் X 1, ..., X 25, X ஐச் சேர்ந்த தற்போக்கு மாதிரி.
எதிர்பார்ப்பு μ இன் தாக்கத்தைப் பெறுவதற்கு ஒரு மதிப்பீட்டைத் தருவதே போதுமானது. சரிவிகிதமான மதிப்பிடுவான் மாதிரி சராசரி:
இந்த மாதிரி காட்டும் முற்றான எடைகள் x 1, ..., x 25, சராசரி:
நாம் மற்றொரு 25 கோப்பைகள் மாதிரியை எடுத்துக்கொண்டால், 250.4 அல்லது 251.1 கிராம்கள் போன்ற மதிப்புக்களை கண்டுபிடிக்க நாம் சுலபமாக எதிர்பார்க்கலாம். இருப்பினும், கோப்பைகளின் சராசரி உள்ளடக்கம் கி்ட்டத்தட்ட 250 கிராம்களுக்கு இருந்தால் 280 கிராம்களின் ஒரு மாதிரி சராசரி மதிப்பு அதிபட்ச அளவிற்கு அரிதானது. முழு இன சராசரியும் உண்மையில் இதே அளவிலான மதிப்பை எடுத்துக்கொள்கிறது என்றால், கண்டுபிடிக்கப்பட்ட தரவு குறிப்பாக வழக்கத்திற்கு மாறானது என்று கருதப்படாததற்குள்ளாக மாதிரி சராசரியின் கண்டுபிடிக்கப்பட்ட 250.2 மதிப்பிற்கு கிட்டத்தட்ட முழு இடைவெளியும் இருக்கும். இதுபோன்ற இடைவெளி μ அளவுருக்கான நம்பக இடைவெளி என்று அழைக்கப்படுகிறது. இதுபோன்ற இடைவெளியை நாம் எவ்வாறு கணக்கிடலாம்? இடைவெளியின் முடிவுப்புள்ளிகள் மாதிரியிலிருந்து கணக்கிடப்பட வேண்டும், இதனால் அவை புள்ளிவிவரங்கள், X 1, ..., X 25 மாதிரியின் செயல்பாடுகள் என்பதோடு அவ்வகையில் அவற்றிற்குள்ளேயான தற்போக்கு மாறுபாடுகளாக இருக்கின்றன.
நம்முடைய விவகாரத்தில், அதே எதிர்பார்ப்பு μ உடன் இயல்பாக பகிர்ந்தளிக்கப்பட்ட இயல்பான பகிர்வு மாதிரியிலிருந்து வரும் X மாதிரி சராசரியை பரிசீலிப்பதன் மூலம் நாம் முடிவுப்புள்ளிகளை தீர்மானிக்கலாம், ஆனால் நிலைப்படுத்தப்பட்ட பிழை σ /√n = 0.5 (கிராம்கள்). நிலைப்படுத்துவதன் மூலம் நாம் பெறும் தற்போக்கு மாறுபாடு
அளவுரு μ மதிப்பிடப்பட வேண்டிதன் அடிப்படையில் அமைந்திருக்கிறது, ஆனால் அளவுரு μ இன் நிலையான இயல்பு பகிர்மான சார்பற்ற நிலையுடன் இருக்கிறது. ஆகவே, μ இன் சார்புநிலையற்ற எண்கள் −z மற்றும் z ஐக் கண்டுபிடிப்பது சாத்தியம், இங்கே Z நம்பக இடைவெளியின் அளவீடு எப்படி இருக்க வேண்டும் என்று நாம் விரும்புகிறோமோ அதன்படி நிகழ்தகவு 1 − α உடன் இடைப்பட்ட நிலையில் இருக்கிறது. நாம் எடுத்துக்கொள்வது 1 − α = 0.95. அதனால் நாம் பெறுவது:
எண் z குவிவு பகிர்மான செயல்பாட்டிலிருந்து பின்பற்றப்படுகிறது:
மேலும் நாம் பெறுவது:
இது பின்வருமாறு விளக்கப்படலாம்: நிகழ்தகவு 0.95 உடன் தற்போக்கு மாறுபாடுகளுக்கு இடையில் உள்ள அளவுரு μ ஐ நாம் எதிர்கொள்வதிலான நம்பக இடைவெளியை நாம் கண்டுபிடிக்கலாம்
அத்துடன்
கணக்கிடப்பட்ட இடைவெளியில் அளவுரு μ ஐ எதிர்கொள்வதன் நிகழ்தகவு 0.95 இருக்கிறது என்பதை இது குறிக்காது. இந்த அளவீடுகள் திரும்ப நிகழ்த்தப்படுகின்ற ஒவ்வொரு முறையும், மாதிரியின் X சராசரிக்கான மற்றொரு மதிப்பாக இருக்கும். 95 சதவிகித நிகழ்வுகளில் μ இந்த சராசரியிலிருந்து கணக்கிடப்படும் முடிவுப்புள்ளிகளுக்கிடையில் இருக்கிறது, ஆனால் 5 சதவிகித நிகழ்வுகளில் இவ்வாறு இல்லை. உண்மையான நம்பக இடைவெளி சூத்திரத்தில் உள்ள அளவிட்ட எடைமானங்களை உள்ளிடுவதன் மூலம் கணக்கிடப்படுகிறது. நம்முடைய 0.95 நம்பக இடைவெளி:

μ இன் விரும்பத்தகுந்த மதிப்பு 250 முடிவாகப் பெற்ற நம்பக இடைவெளிக்குள்ளாக இருக்கிறது, இயந்திரம் தவறாக சரிசெய்துகொள்கிறது என்பதை நம்புவதற்கு எந்தக் காரணமும் இல்லை.
கணக்கிடப்பட்ட இடைவெளியானது μ இடைநிலையில் (அல்லது இல்லாமல்) இருக்கக்கூடியவிடத்தில் நிலையான முடிவுப்புள்ளிகளைக் கொண்டிருக்கிறது. ஆகவே இந்த நிகழ்வு 0 அல்லது 1 என்ற நிகழ்தகவைக் கொண்டிருக்கிறது. "(1 − α) நிகழ்தகவால் அளவுரு μ நம்பக இடைவெளியில் இருந்துகொண்டிருக்கிறது" என்றும் நம்மால் கூற முடியாது . μ கணக்கிடப்பட்ட இடைவெளிக்குள்ளாக இருக்கும் என்ற நிகழ்வுகளின் 100(1 − α) % இல் திரும்ப நிகழ்த்தல்கள் மூலமே என்பதை மட்டுமே நாம் தெரிந்துகொள்கிறோம். இருப்பினும் 100α % நிகழ்வுகளில் இப்படி இருப்பதில்லை. அத்துடன் எதிர்பாராதவிதமாக இந்த நிகழ்வுகளில் உள்ள எதில் இது நடக்கிறது என்பதும் நமக்குத் தெரிவதில்லை. அதனால்தான் நாம் கூறுகிறோம்: "நம்பக இடைவெளி 100(1 − α) % உடன், μ நம்பக இடைவெளியில் இருந்துகொண்டிருக்கிறது."
வலதுபக்கம் இருக்கும் எண்கள் கொடுக்கப்பட்ட இன சராசரி μக்கான நம்பக இடைவெளியின் 50 மெய்ப்படுத்தல்களைக் காட்டுகிறது. நாம் தற்போக்காக ஒரு மெய்ப்படுத்தலை தேர்வுசெய்தால், நிகழ்தகவு 95% இல் நாம் முடிக்கிறோம் என்பது அளவுருவைக் கொண்டிருக்கும் இடைவெளியை தேர்வுசெய்கிறது; இருப்பினும் நாம் அதிர்ஷ்டமில்லாவதவர்களாகவும், தவறான வழியைத் தேர்வுசெய்பவர்களாகவும் இருக்கிறோம். நமக்குத் தெரியப்போவதில்லை; நாம் நம்முடைய இடைவெளியில் மாட்டிக்கொண்டிருக்கிறோம்.
கோட்பாட்டு உதாரணம்[தொகு]
ஒருவேளை X 1, ..., X n ஆகியவை (அளவுருக்கள்) சராசரி μ மற்றும் மாறுபாடு σ2 உடன் இயல்பு பகிர்மான இனத்திலிருந்து பெறப்படும் சார்பற்ற மாதிரி என்றால். கொள்க
நன்கறியப்பட்ட புள்ளிவிவரங்களில், மாதிரி சராசரி மற்றும் மாதிரி மாறுபாடு.
பின்னர்
n − 1 பாகைகள் தனிப்பட்டதோடு மாணாக்கரின் டி-பகிர்மானத்தைக் கொண்டிருக்கிறது. T இன் பகிர்மானம் கண்டுபிடிக்கப்படாத அளவுருக்கள் μ மற்றும் σ 2 இன் மதிப்புக்களை சார்ந்திருக்காது என்பதை கவனிக்கவும்; அதாவது., இது ஒரு இருசு அளவு. ஒருவேளை நாம் μ க்கான 90% நம்பக இடைவெளியைக் கணக்கிட வேண்டும் என்றால். எனவே, c ஐ பகிர்மானத்தின் 95வது சதவிகிதத்திலானது என்று குறிப்பிடுவது.
- பாகுபடுத்தல் தோல்வி (தொடரமைப்புத் தவறு): {\displaystyle \Pr\left(-c}
(குறிப்பு: "95வது" மற்றும் "0.9" ஆகியவை முந்தைய வெளிப்பாடுகளில் சரியாக இருக்கின்றன. T ஆனது −c ஐக் காட்டிலும் குறைவாக இருக்கும் என்பதற்கு 5 சதவிகித வாய்ப்பு இருக்கிறது, இது +c ஐக் காட்டிலும் பெரிதாக இருக்கும் என்பதற்கு 5 சதவிகித வாய்ப்பிருக்கிறது. ஆகவே, T ஆனது −c மற்றும் +c க்கு இடையில் இருக்கும் என்பதற்கான நிகழ்தகவு is 90%.)
தொடர்விளைவாக
- பாகுபடுத்தல் தோல்வி (தொடரமைப்புத் தவறு): {\displaystyle \Pr\left(\overline{X} - \frac{cS}{\sqrt{n}} }
நமக்கு μ க்கான கோட்பாட்டு 90% நம்பக இடைவெளி இருக்கிறது.
இந்த மாதிரியைக் கண்டுபிடித்த பின்னர் Xக்கான x மதிப்புக்களையும், S க்கான s ஐயும் நாம் கணக்கிட்ட நம்பக இடைவெளியிலிருந்து கணக்கிடுகிறோம்.
முடிவுப்புள்ளிகளாக உள்ள நிலையான எண்களுடனான இடைவெளி, இதில் அளவுரு μ ஐக் கொண்டிருக்கும் ஒரு குறிப்பிட்ட நிகழ்தகவு இருக்கிறது என்றும் நம்மால் இனிமேலும் கூறமுடியாது. μ இந்த இடைவெளியில் இருக்கலாம் அல்லது இல்லாமல் இருக்கலாம்.
கருதுகோள் சோதனைக்குள்ள உறவு[தொகு]
நம்பக இடைவெளிகள் மற்றும் புள்ளிவிவர கருதுகோள் சோதனை கருத்தாக்கங்களின் உருவாக்கங்கள் தனித்துவமாக இருக்கையில் அவை ஒருசில அளவிற்கு சார்புள்ளவையாகவும் ஒருசில அளவிற்கு குறைநிரப்பலாகவும் இருக்கிறது. இதே முறையில் எல்லா நம்பக இடைவெளிகளையும் கட்டமைக்க முடியாது என்ற நிலையில், நம்பக இடைவெளிகளைக் கட்டமைப்பதற்கான ஒரு பொது நோக்க அணுகுமுறை 100α% சிறப்பு அளவில் நிராகரிக்கப்படாத கருதுகோள் θ=θ0 இன் சோதனைக்குரிய θ0 மதிப்புக்கள் அனைத்தையும் உள்ளிட்டிருக்கும் 100(1−α)% நம்பக இடைவெளியை வரையறுப்பதேயாகும். இதுபோன்ற அணுகுமுறையானது பொருத்தமான சிறப்பு சோதனையின் நடைமுறை கிடைப்புத்தன்மையை முன்னூகிக்கிறது என்பதால் எப்போதும் கிடைக்கக்கூடியவையாக இல்லாமல் போகலாம். இயல்பாகவே, சிறப்பு சோதனைக்கு தேவைப்படும் எந்த அனுமானங்களும் நம்பக இடைவெளிகளுக்கு மேலாகவே எடுத்துச்செல்லப்படும்.
நம்பக இடைவெளிக்குள்ளாக இருக்கும் அளவுரு மதிப்புக்கள் கருதுகோள் சோதனையால் நிராகரிப்பட முடியாத மதிப்புக்களுக்கு சமமானதாக இருக்கும் என்ற பொதுத் தொடர்பியலை உருவாக்கிக்கொள்வது சௌகரியமானதாக இருக்கலாம், ஆனால் இது அபாயகரமானது. பல நிகழ்வுகளிலும் மேற்கோளாக காட்டப்படும் நம்பக இடைவெளிகள் தோராயமான ஏற்பை மட்டுமே கொண்டிருக்கின்றன, அநேகமாக "நிலையான பிழைக்கு இருமடங்காக கூட்டுதல் அல்லது கழித்தலிலிருந்து" பெறப்படுவதாக இருக்கிறது, அத்துடன் கருதுகோள் சோதனைகளுக்கு தொடர்புகொண்டதாயிருக்கக்கூடிய இதனுடைய தாக்கங்கள் வழக்கமாக அறியப்படாததாக இருக்கிறது.
பொருளும் விளக்கமும்[தொகு]
பொதுமைப்படுத்தல் முறைகளின் பயன்பாட்டாளர்களுக்கு, நம்பக இடைவெளி குறித்த பல்வேறு விளக்கங்கள் வழங்கப்படுகின்றன.
- நம்பக இடைவெளி மாதிரிகள் வெளிப்படுத்தப்படுவதாக இருக்கலாம் (அல்லது திரும்ப நிகழும் மாதிரிகள்): "இந்த நடைமுறை பலதரப்பட்ட மாதிரிகளில் திரும்ப நிகழ்த்தப்பட்டதாக இருந்தால், கணக்கிடப்பட்ட நம்பக இடைவெளி (ஒவ்வொரு மாதிரிக்கும் மாறுபடுவது) நேரத்தின் 90% உண்மை அளவுருவை உடனிணைத்துக்கொண்டதாக இருக்கும்". [5] இது அதே இனத்தைச் சேர்ந்த திரும்ப நிகழும் மாதிரியாக்கமாக இருக்க வேண்டியதில்லை, திரும்ப நிகழும் மாதிரியாக்கம் மட்டுமே என்பதை கவனிக்கவும் [6].
- நம்பக இடைவெளியின் விளக்கம் பின்வருவதுபோன்ற ஒன்றிற்கு சேர்த்துக்கொள்ளப்படுவதாக இருக்கலாம்: "10% அளவில் புள்ளிவிவரரீதியில் முக்கியத்துவம் அல்லாத அளவுரு மற்றும் கண்டுபிடிக்கப்பட்ட மதிப்பீட்டிற்கு இடையிலான வித்தியாசத்திற்குரிய இன அளவுவிற்கேற்ற மதிப்புக்களை நம்பக இடைவெளி குறிக்கிறது" [7]. உண்மையில், இது நம்பக இடைவெளி கட்டமைக்கப்படுகின்ற ஒரு குறிப்பிட்ட வழியோடு இது தொடர்புகொண்டதாக இருக்கிறது.
- இதே பொருளில் ஆய்வுப் பொருள்கள் உருவாக்கப்படுவதற்கான கையாளுதல்களின் தற்போக்கு ஒதுக்கீட்டிற்குரிய விவாதங்களில் நம்பக இடைவெளியோடு தொடர்புகொண்டுள்ள நிகழ்தகவும் முன்-பரிசோதனை கண்ணோட்டத்தைச் சேர்ந்ததாக கருதப்படலாம். இங்கே பரிசோதனையாளரானவர் நம்பக இடைவெளியை கணக்கிடுவதற்கான வழியை அமைக்கிறார் என்பதோடு, அவர்கள் உண்மையான பரிசோதனையை மேற்கொள்ளும் முன்பு அவர்கள் முடிவிற்கு வந்த நம்பக இடைவெளி உண்மையான ஆனால் அறியப்படாத மதிப்பை உள்ளிடுவதற்கான வாய்ப்பைக் கொண்டிருக்கிறது என்பதை அறிந்துகொள்கின்றனர்.[8] இது மேலே உள்ள "திரும்ப நிகழும் மாதிரி" விளக்கத்தோடு மிகவும் ஒத்துப்போவதாக இருக்கிறது, எந்த அர்த்தமுள்ள பொருளிலும் திரும்ப நிகழ்த்தப்பட இயலாததாக இருக்கும் மாதிரியாக்க நடைமுறையின் அனுமான திரும்ப நிகழ்தல்களை பரிசீலப்பதில் நம்பிக்கை வைப்பதை தவிர்ப்பது தவிர்த்து. பார்க்க நேமன் கட்டமைப்பு.
மேலே உள்ள ஒவ்வொன்றிற்கும் பின்வருவது பொருந்துகிறது: கணக்கிடப்பட்டவுடன் அளவுருவின் உண்மை மதிப்பு 90% நம்பக இடைவெளிக்கு வெளியில் இருக்கிறது என்றால், பின்னர் இந்த நிகழ்வு எதிர்பாராமல் நிகழும் 10% (அல்லது குறைவான) நிகழ்தகவைக் கொண்டிருக்கும் நிகழ்வு ஏற்படலாம்.
"நம்பகம்" என்ற சொற்பதத்தின் பொருள்[தொகு]
"நம்பகம்" என்ற வார்த்தையின் பொதுவான பயன்பாட்டிற்கும் புள்ளிவிவர பயன்பாட்டிற்கும் இடையில் வித்தியாசம் இருக்கிறது, இது துறைசாராதவர்களுக்கு எப்போதுமே குழப்பமான ஒன்றுதான் என்பதோடு இது நம்பக இடைவெளிகளின் விமர்சனங்களுள் ஒன்றாக இருக்கிறது, அதாவது புள்ளிவிவர துறை அல்லாதவர்களின் பயன்பாட்டில் இந்த "நம்பகம்" என்பது தவறாக வழிகாட்டுவதாகவே இருக்கிறது.
பொதுவான பயன்பாட்டில், ஏதோ ஒன்றிலான 95% நம்பகம் என்பது வழக்கமாக தோற்றவியல் நிச்சயத்தன்மையைக் குறிப்பிடுவதாகவே எடுத்துக்கொள்ளப்படுகிறது. புள்ளிவிவரங்களில், 95% நம்பகம் என்பது இருபது அல்லது அதற்கும் குறைவானவற்றில் ஒருமுறை மட்டுமே நிகழ்கின்ற ஏதோ ஒரு நிகழ்வை ஆராய்ச்சியாளர் காண்கின்றார் என்பதை மட்டுமே குறிக்கிறது. ஒரு இரண்டு தாயங்களை உருட்டி இரட்டை ஆறுகளைப் பெறுகிறார் என்றால் (1/36 என்ற மடங்கில் ஏற்படுவது, அல்லது ஏறத்தாழ 3%), ஒருசிலர் அந்த தாயம் நிர்ணயிக்கப்பட்டது என்பதையே நிரூபிக்கிறது என்று கூறலாம், இருப்பினும் புள்ளிவிவரரீதியில் பேசினால் அவை இருக்கும் 97% நம்பக இடைவெளியைக் கொண்டிருக்கலாம். இதேபோல், 95% நம்பகத்தில் ஒரு புள்ளிவிவர இணைப்பு நிரூபணம் அல்லது, சிறந்த ஆதாரமும் அல்ல, அதாவது இணைக்கப்பட்டுள்ள விஷயங்களுக்கிடையில் எந்த உண்மையான தொடர்பும் இல்லை.
ஒரு ஆய்வு பலதரப்பட்ட புள்ளிவிவர சோதனைகளோடு சம்பந்தப்பட்டிருக்கும்போது, சில துறைசாராதவர்கள் தனிப்பட்ட சோதனைகள் என்பவை ஒருவர் ஆய்விலேயே கொண்டிருக்க வேண்டிய முடிவுகளில் உள்ள நம்பகம் என்பதோடு தொடர்புகொண்டிருக்கிறது என்று அனுமானிக்கலாம். உண்மையில், ஒரு ஆய்வின்போது நடத்தப்படும் புள்ளிவிவர சோதனைகள் அனைத்தின் முடிவுகளும் அது உருவாக்கும் நேர்மறை இணைப்புகளில் எந்த நம்பகத்தை ஒருவர் அமைக்கிறார் என்ற தீர்மானத்தில் முழுமையாக தீர்மானிக்கப்பட வேண்டும். உதாரணத்திற்கு, 95% நம்பகத்தில் 40 புள்ளிவிவர சோதனைகளோடு சம்பந்தப்பட்டிருக்கிற, 3 நேர்மறை முடிவுகளை உருவாக்குகின்ற ஆய்வு மேற்கொள்ளப்படுகிறது என்போம். ஒவ்வொரு சோதனையும் தவறான நேர்மறைகளை உருவாக்கும் 5% வாய்ப்பைக் கொண்டிருக்கிறது, இதனால் இதுபோன்ற ஆய்வு தோராயமாக மூன்றில் இரண்டு என்ற 3 தவறான நேர்மறைகளை உருவாக்கும். இவ்வாறு ஆய்வின் நேர்மறை முடிவுகளின் எந்த ஒன்றிலும் ஒருவர் கொண்டிருக்கக்கூடிய நம்பகமானது கிட்டத்தட்ட 32% வரை மட்டுமே சரியானது, இது ஆராய்ச்சியாளர்கள் தங்களுடைய ஏற்புத் தரநிலையாக அமைத்துக்கொள்ளக்கூடிய 95% கீழே இருக்கிறது.
மாற்றுக்களும் விமர்சனங்களும்[தொகு]
நம்பக இடைவெளிகள் என்பவை இடைவெளி மதிப்பீட்டின் ஒரு முறை என்பதோடு பொதுமைப்படுத்தல் புள்ளிவிவரங்களில் இது தொடர்ச்சியாக பயன்படுத்தப்படுகிறது. பேஸியன் புள்ளிவிவரங்களிலான ஒரு ஒப்புமைக் கருத்தாக்கம் நம்பந்தகுந்த இடைவெளிகளாகும், அதேநேரம் மாற்று பொதுமைப்படுத்த முறை, அளவுருக்களை மதிப்பிடுவதைக் காட்டிலும் எதிர்கால மாதிரிகளின் முடிவை மதிப்பிடுகின்ற முன்னூகிப்பு இடைவெளி.
இந்த முறைகளில் எது மிகவும் பயன்மிக்க முடிவுகளை உருவாக்குகிறது என்பது குறித்து உடன்பாடின்மை இருக்கிறது: இந்தக் கணக்கீடுகளின் கணிதங்கள் அரிதாகவே கேள்வி எழுப்பப்படுகின்றன – மாதிரியாக்க பகிர்மானங்களின் அடிப்படையிலானதாக அமைந்திருக்கும் நம்பக இடைவெளிகள், நம்பத்தகுந்த இடைவெளிகள் பேயஸ் தேற்றத்தை அடிப்படையாகக் கொண்டவையாக இருக்கின்றன – ஆனால் இந்த முறைகளின் பயன்பாடுகள், பயனீடு மற்றும் உருவாக்கப்பட்ட புள்ளிவிவரங்களின் விளக்கம் விவாதிக்கப்படுகிறது.
பேஸியன் முறைகளின் பயன்படுத்துநர்கள், அவர்கள் இடைவெளி மதிப்பீட்டை உருவாக்கினார்கள் என்றால் அது நம்பக இடைவெளிகளுக்கு முரணானதாக இருக்கும், "அளவுரு உண்மையில் இந்த இடைவெளியில் இருக்கையில் என் நம்பிக்கையின் அளவு 90% "[9] என்று கூற விரும்பினால், முன்னூகிப்பு இடேவெளிகளின் பயனர்கள் அதற்குப் பதிலாக கூறுவார்கள் "அடுத்த மாதிரியானது காலத்தின் 90% இடைவெளிக்குள்ளாக இருக்கும் என்று நான் முன்னூகிக்கிறேன் ."
நம்பக இடைவெளிகள் நிகழ்தகவின் வெளிப்பாடுகள் என்பதுடன் நிகழ்தகவின் இயல்பான விதிகளுக்குட்பட்டவை. சில புள்ளிவிவரங்கள் நம்பக இடைவெளியோடு வழங்கப்பட்டிருந்தன என்றால், ஒவ்வொன்றும் சார்பற்றிருப்பதன் அனுமானத்தில் தனித்தனியாக கணக்கிடப்படும், இந்த அனுமானத்திற்கு மதிப்பளிக்கப்பட வேண்டும் என்பதோடு கணக்கீடுகள் மதிப்பற்றதையே வழங்கும். உதாரணத்திற்கு, குறுகலான இடைவெளியுடன் கூடிய புள்ளிவிவரம் கவனத்திற்கு கொண்டுவரப்பட்டால் அந்த இடைவெளி அந்த புள்ளிவிவரத்திற்கான உண்மை இடைவெளியாக அதற்கு மேலும் இருக்காது. தேர்வு நடவடிக்கை நிகழ்தகவை மாற்றும் என்பதோடு இந்த நிகழ்வில் அது இடைவெளியை அகலப்படுத்துகிறது.
புள்ளிவிவர சோதனைகளை மேற்கொள்வதற்கு நம்பக இடைவெளிகள் உருவாக்கப்பட்டிருக்கும்போது இது முக்கியத்துவம் வாய்ந்ததாகிறது. பலதரப்பட்ட சோதனைகள் செய்யப்பட்ட இந்த முடிவாக கிடைக்கும் நேர்மறை முடிவுகள் அவற்றிலிருந்து தேர்வுசெய்யப்பட்டால் இந்த சோதனையை நடத்த பயன்படுத்தப்பட்ட இடைவெளிகள் மாறும், அத்துடன் பெரும்பாலான சூழ்நிலைகளில் இந்த சோதனை மதிப்பற்றதையே வழங்கும்.
சரிவிகிதங்களுக்கும் தொடர்புடைய அளவுகளுக்கும் இடையில் உள்ள நம்பக இடைவெளிகள்[தொகு]
மாதிரி அளவும் எண்ணிக்கையும் போதுமான அளவிற்கு பெரியதாக இருந்தால், இன சராசரிக்கான ஒரு தோராயமான நம்பக இடைவெளி மைய வரம்புத் தேற்றத்தில் நம்பிக்கை வைத்து இனத்தில் இயல்பாக் பகிரப்படாத தற்போக்கு மாறுபாடுகளுக்கேற்ப கட்டமைக்கப்படலாம். இந்த சூத்திரம் மேலே உள்ள நிகழ்விற்கு பொருத்தமானது (மாதிரி சராசரி இன சராசரிக்கு உண்மையில் இயல்பாக பகிரப்படுமிடத்தில்). இந்தத் தோராய அளவானது, தற்போக்கு மாறுபாட்டின் நிகழ்தகவு பகிர்மானம் இயல்பான பகிர்மானத்திலிருந்து மிகவும் மாறுபட்டிருக்கவில்லை என்றால் மாதிரியிலான ஒருசில டசன் கண்டுபிடிப்புகளோடு மட்டுமே இது முற்றிலும் சரியானதாக இருக்கும் (எ.கா. இதனுடைய குவிவு பகிர்மானச் செயல்பாடு எந்தத் தொடர்ச்சியின்மைகளையும் கொண்டிருக்கவில்லை என்பதோடு இதனுடைய கோணல் மிதமானதாக இருக்கிறது).
ஒரு வகையான மாதிரி சராசரி, மதிப்பு 1 ஐ உண்மையானதாகவும் மதிப்பு 0 ஐ தவறானதாகவும் எடுத்துக்கொள்கின்ற குறிப்பீட்டு மாறுபாடுகளின் சராசரியாகும். இதுபோன்ற மாறுபாட்டின் சராசரி ஒன்றுக்கு சமமானதாக உள்ள மாறுபாட்டைக் கொண்டிருக்கும் சரிவிகிதத்திற்கு சமமானதாக இருக்கிறது (இனம் மற்றும் எந்த மாதிரியிலும் இருக்கின்ற இரண்டும்). இது குறிப்பீட்டு மாறுபாட்டின் பயன்மிக்க உடைமைப்பொருளாகும், குறிப்பாக அனுமான சோதனைக்கு. மைய வரம்புத் தேற்றத்தைப் பயன்படுத்துவதற்கு, ஒரு பெரிய அளவிற்கு போதுமான மாதிரியைப் பயன்படுத்த வேண்டும். கடுமையான கட்டைவிரல் சட்டம் என்பது குறிப்பீடு 1 ஆக இருக்கின்ற மற்றும் குறைந்தபட்சம் 0 ஆக இருப்பதில் 5 ஆக இருக்கின்றவற்றை ஒருவர் பார்க்க வேண்டும் என்பதாகும். மேலே உள்ள சூத்திரத்தைப் பயன்படுத்தி கட்டமைக்கப்படும் நம்பக இடைவெளிகள் எதிர்மறை எண்கள் அல்லது 1க்கும் அதிகமான எண்களை உள்ளிட்டிருக்கலாம், ஆனால் சரிவிகிதங்கள் எதிர்மறையாகவோ அல்லது 1க்கு அதிகமாகவோ இருக்க இயலாது. மேலும், மாதிரி சரிவிகிதங்கள மதிப்புக்களின் முற்று எண்ணை மட்டுமே எடுத்துக்கொள்ள முடியும், இதனால் மைய வரம்புத் தேற்றம் மற்றும் இயல்புப் பகிர்மானம் ஆகியவை நம்பக இடைவெளியை உருவாக்குவதற்கான சிறந்த கருவிகள் அல்ல. பார்க்க இந்த நிகழ்விற்கு சிறந்த முறைகளாக இருக்கும் "ஈருறுப்பு சரிவிகித நம்பக இடைவெளி".
மேலும் காண்க[தொகு]
- பி-மதிப்பு
- நம்பகப் பகுதி
- பிழை சட்டம்
- முன்னூகிப்பு இடைவெளி
- ஏற்பு இடைவெளி
- பூட்ஸ்ட்ராப்பிங் (புள்ளிவிவரம்)
- ஈருறுப்பு சரிவிகித நம்பக இடைவெளி
- திடமான நம்பக இடைவெளிகள்
- செபிஷேவின் சமனின்மை
- இடைவெளி முற்று கூறுகள்
ஆன்லைன் கணக்கிடு கருவிகள்[தொகு]
- டிஏஎம்யுவின் நம்பக இடைவெளி கணக்கிடு கருவிகள் பரணிடப்பட்டது 2010-06-15 at the வந்தவழி இயந்திரம்
- கிராப்பேட் குயிக்கால்க்ஸ்
குறிப்புகள்[தொகு]
- ↑ கோல்ஸ்டீன், ஹெச்., & ஹீலே, எம்.ஜே.ஆர். (1995). "சராசரிகள் தொகுப்பின் வரைவட வழங்கல்." ஜர்னல் ஆஃப் தி ராயல் ஸ்டேடிஸ்டிக்ஸ் சொசைட்டி , 158 , 175–77.
- ↑ Wolfe R, Hanley J (Jan 2002). "If we're so different, why do we keep overlapping? When 1 plus 1 doesn't make 2". CMAJ 166 (1): 65–6. பப்மெட்:11800251. பப்மெட் சென்ட்ரல்:99228. http://www.cmaj.ca/cgi/pmidlookup?view=long&pmid=11800251.
- ↑ ஜார், ஜே.ஹெச். (1984) பயோஸ்டேடிஸ்டிகல் அனாலிஸிஸ். பிரிண்டைஸ் ஹால் இண்டர்நேஷனல், நியூ ஜெர்ஸி. பக் 43–45
- ↑ Bernardo JE, Smith, Adrian (2000). Bayesian theory. New York: Wiley. பக். 259. பன்னாட்டுத் தரப்புத்தக எண்:0-471-49464-X.
- ↑ காக்ஸ் டிஆர், ஹிங்க்லே டிவி. (1974) தியோராட்டிகல் ஸ்டேடிஸ்டிக்ஸ், சாப்மன் & ஹால், பக்49, 209
- ↑ கெண்டல், எம்.ஜி. மற்றும் ஸ்டூவர்ட், டி.ஜி. (1973) தி அட்வான்ஸ்டு தியரி ஆஃப் ஸ்டேடிஸ்டிக்ஸ். தொகுப்பு 2: இன்ஃப்ரன்ஸ் அண்ட் ரிலேஷன்ஷிப், கிரிஃபின், லண்டன். பிரிவு 20.4
- ↑ காக்ஸ் டிஆர், ஹின்க்லி டிவி. (1974) தியரேட்டிக்கல் ஸ்டேடிஸ்டிக்ல், சாப்மன் & ஹால், பக்214, 225, 233
- ↑ நேமன், ஜே. (1937) "நிகழ்தகவின் உன்னதக் கோட்பாட்டின் அடிப்படையில் அமைந்த புள்ளிவிவர மதிப்பீட்டுக் கோட்பாட்டின் உருவரை", ஃபிலசாபிகல் டிரான்சாக்ஸன்ஸ் ஆஃப் தி ராயல் சொசைட்டி ஆஃப் லண்டன் ஏ, 236, 333–380.
- ↑ காக்ஸ் டிஆர், ஹின்க்லி டிவி. (1974) தியராட்டிக்கல் ஸ்டேடிடிக்ஸ், சாப்ளின் & ஹால், p390
குறிப்புதவிகள்[தொகு]
- பிஷர், ஆர்.ஏ. (1956) ஸ்டேட்டிஷ்டிகல் மெத்தேட்ஸ் அண்ட் சயின்டிஃபிக் இன்ஃபெரன்ஸ். ஆலிவர் அண்ட் பாய்ட், எடின்பர்க். (பார்க்க பக். 32.)
- ஃபிராய்ட், ஜே.இ. (1962) மேத்தமேட்டிக்கல் ஸ்டேடிடிக்ஸ் பிரண்டைஸ் ஹால், எங்கல்வுட் கிளிஃப்ஸ், என்ஜே. (பார்க்க பக். 227–228.)
- ஹேக்கிங், ஐ. (1965) லாஜிக் ஆஃப் ஸ்டேடிஸ்டிக்கல் இன்ஃபரன்ஸ். கேம்ப்ரிட்ஜ் யுனிவர்சிட்டி பிரஸ், கேம்ப்ரிட்ஜ்.
- கீப்பிங், இ.எஸ். (1962) இண்ட்ரடக்ஷன் டு சயின்டிஃபிக் இன்ஃபரன்ஸ். டி. வான் நாஸ்ட்ரண்ட், பிரின்ஸ்டன், என்ஜே.
- கீஃபர், ஜே. (1977) "கண்டிஷனல் கான்ஃபிடன்ஸ் ஸ்டேட்மெண்ட்ஸ் அண்ட் கான்ஃபிடன்ஸ் எஸ்டிமேட்டர்ஸ் (விவாதத்தோடு)" ஜர்னல் ஆஃப் தி அமெரிக்கன் ஸ்டேடிஸ்டிக்கல் அசோஸியேஷன், 72, 789–827.
- நேமன், ஜே. (1937) "அவுட்லைன் ஆஃப் எ தியரி ஆஃப் ஸ்டேடிஸ்டிகல் எஸ்டிமேஷன் பேஸ்டு ஆன் தி கிளாஸிக்கல் தியரி ஆஃப் பிராபபிலிட்டி" ஃபிலசாபிகல் டிரான்ஸாக்ஷன்ஸ் ஆஃப் தி ராயல் சொசைட்டி ஆஃப் லண்டன் ஏ, 236, 333–380. (தழுவல் படைப்பு.)
- ராபின்ஸன், ஜி.கே. (1975) "சம் கவுண்டர்எக்ஸாம்பிள்ஸ் டு தி தியரி ஆஃப் கான்ஃபிடன்ஸ் இண்டர்வல்ஸ்." பயோமெட்ரிகா, 62, 155–161.
- ரெய்சிகல் ஜே. (2003) கான்ஃபிடன்ஸ் இண்டர்வெல் ஃபார் தி பயோனாமினல் பாராமீட்டர்: சம் நியூ கன்சிடரேஷன்ஸ். ஸ்டேடிஸ்டிக்ஸ் இன் மெடிசின், 22, 611–621.
- ரெய்சிகல் ஜே., அபோனிய்-டோத் இஸட்., & சிங்கர் ஜே. (2008) இரண்டு ஈருறுப்பு சரிவிகிதங்களுக்கான துல்லிய நம்பக அலகு மற்றும் வேறுபாடு மற்றும் சரிவிகிதஙகளுக்கான நிபந்தணையற்ற நம்பக இடைவெளிகள்[தொடர்பிழந்த இணைப்பு]. கம்ப்யூட்டேஷனல் ஸ்டேட்டிஸ்டிக்ஸ் & டேட்டா அனாலிஸிஸ், 52, 5046–5053.
- ஸ்மித்ஸன், எம். (2003) கான்ஃபிடன்ஸ் இண்டர்வல்ஸ் . குவாண்டிடேடிவ் அப்ளிகேஷன்ஸ் இன் தி சோஸியல் சயின்ஸ் சீரிஸ், எண். 140. பெல்மண்ட், சிஏ: சேஜ் பப்ளிகேஷன்ஸ். பன்னாட்டுத் தரப்புத்தக எண் 1-85227-092-6
புற இணைப்புகள்[தொகு]
- எக்ஸலிஸ் செயல்படும் நம்பக இடைவெளிகள் பயிற்சி நிரல்களுக்கான கண்டுபிடிப்பு மென்பொருள் பரணிடப்பட்டது 2011-11-22 at the வந்தவழி இயந்திரம்
- ஆர்-சதுக்கங்கள் பரணிடப்பட்டது 2009-07-03 at the வந்தவழி இயந்திரம், தொடர்புப்போக்கு குணகங்கள் பரணிடப்பட்டது 2009-08-06 at the வந்தவழி இயந்திரம், மற்றும் தொடர்புபோக்கு இடையீடுகளுக்கான பரணிடப்பட்டது 2009-04-04 at the வந்தவழி இயந்திரம் நம்பக இடைவெளி கணக்கிடு கருவிகள்.
- Weisstein, Eric W., "Confidence Interval", MathWorld.
- CAUSEweb.org நம்பக இடைவெளிகள் உட்பட புள்ளிவிவரங்களைக் கற்றுத்தருவதற்கான பலதரப்பட்ட மூலாதாரங்கள்.
- நம்பக இடைவெளிகளுக்கான ஒரு ஒருங்கிணைப்பு அறிமுகம்
- கான்ஃபிடன்ஸ் இண்டர்வல்ஸ்: கான்ஃபிடன்ஸ் லெவல், சாம்பிள் சைஸ், அண்ட் மார்ஜின் ஆஃப் எர்ரர் எரிக் ஷுல்ஸ், வோல்ஃப்ராம் டெமான்ஸ்ட்ரேஷன்ஸ் புராஜக்ட்.












![{\displaystyle {\begin{aligned}\Phi (z)&=P(Z\leq z)=1-{\tfrac {\alpha }{2}}=0.975,\\[6pt]z&=\Phi ^{-1}(\Phi (z))=\Phi ^{-1}(0.975)=1.96,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c52fc78784c9bbf0e1be15f2625abebb469eca27)
![{\displaystyle {\begin{aligned}0.95&=1-\alpha =P(-z\leq Z\leq z)=P\left(-1.96\leq {\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}\leq 1.96\right)\\[6pt]&=P\left({\bar {X}}-1.96{\frac {\sigma }{\sqrt {n}}}\leq \mu \leq {\bar {X}}+1.96{\frac {\sigma }{\sqrt {n}}}\right)\\[6pt]&=P\left({\bar {X}}-1.96\times 0.5\leq \mu \leq {\bar {X}}+1.96\times 0.5\right)\\[6pt]&=P\left({\bar {X}}-0.98\leq \mu \leq {\bar {X}}+0.98\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/206e45b362576d87d1e53d8f539af48cced916a1)






![{\displaystyle \left[{\overline {x}}-{\frac {cs}{\sqrt {n}}},{\overline {x}}+{\frac {cs}{\sqrt {n}}}\right],\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d429a0286ba259bd4a54b3ee7b9572fd3db750ac)