போல்யா எண்ணெடுப்புத் தேற்றம்

போல்யா எண்ணெடுப்புத் தேற்றம் (Polya Enumeration Theorem) என்பது சேர்வியலில் ஒரு சிறப்புத் தேற்றம். இது கோல நூலில் கோலங்களை எண்ணல், வேதியலில் மாற்றியங்களை எண்ணல், சமச்சீர் உள்ள இடங்களிலெல்லாம் சமச்சீரினால் ஏற்படும் எண்ணிக்கைக் குழப்பங்களை விடுவித்தல், போன்ற பல எண்ணிக்கைப் பற்றிய கேள்விகளுக்கு (பிரச்சினைகளுக்கு) அபூர்வமான முறையில் தீர்வு வகுக்க உதவுகின்றது. அதனால் கணிதத்துறையைத் தாண்டி இயற்பியல், சமூகவியல் போன்ற மற்றதுறைகளிலும் பயன்படும் தேற்றமிது. 1927 இல் முதன்முதல் ரெட்ஃபீல்ட் என்பவரால் கண்டுபிடிக்கப்பட்ட போதிலும் கணிதவியலர்களுக்கும் கூட நன்கு பிடிபடாத காரணத்தால் கவனிக்கப்படாமல் இருந்து, பிறகு 1937ல் ஜியார்ஜ் போல்யா வினால் அடிப்படையிலிருந்து தொடங்கி ஒரு பெரிய தேற்றமாக நிறுவப்பட்டு பற்பல பயன்பாடுகளுக்கும் செயல்பட வழிவகுப்பட்டது. அன்றிலிருந்து இத்தேற்றமும் அதன் பயன்பாடுகளும் சேர்வியலில் முக்கிய பங்கு வகிக்கின்றது. இதை ரெட்ஃபீல்ட்-போல்யா தேற்றம் (Redfield-Polya Theorem) என்றும் சொல்வர்.

போல்யா தேற்றம்

கருதுகோள்:

$D,R$ என்பவை இரு முடிவுறு கணங்கள். $R$ இலுள்ள ஒவ்வொரு $r$ க்கும் $w(r)$ என்ற ஓர் எடை வரையறுக்கப்படுகிறது. பொதுவாக இவ்வெடை விகிதமுறு எண் களைக்கொண்டு உண்டாக்கப்பட்ட ஒரு பரிமாற்று இயற் கணிதத்தின் உறுப்பு என்று கொள்ளலாம். குறிப்பாக அது ஒரு விகிதமுறு எண்ணாகவே இருக்கலாம்.

$G$ என்பது $D$ இனுடைய உறுப்புகளின் ஒரு வரிசைமாற்றுக் குலம்.

$R^{D}=\{f:D\rightarrow R\};$ அதாவது, $R^{D}$ என்பது $D$ இலிருந்து $R$ க்குப்போகும் எல்லா கோப்புகளின் கணம்.

இந்த கணத்தில் $G$ ஐக்கொண்டு ஒரு சமான உறவு உண்டாக்குவோம்:

$f_{1},f_{2}$ ஆகிய இரு கோப்புகள் சமானம் என்ச்சொல்லப்படுவதற்கு இலக்கணம்: $f_{1}g=f_{2}$ என்றிருக்கும்படி $G$ இல் ஒரு $g$ உள்ளது.

இவ்வுறவு $R^{D}$ ஐ பல 'மாதிரி'களாகப் பிரிக்கிறது.

G இன் சுழற்குறிப்பீட்டை $Z(G;s_{1},s_{2},s_{3},...)$ என்று குறிப்போம்.

(G இன் சுழற்குறிப்பீடு என்பது G இலுள்ள உறுப்புகளின் சுழலமைப்புகளை உறுப்புகளாகக்கொண்ட பல்லுறுப்புக்கோவை).

முடிவு:

$R^{D}$ இல் ஏற்படும் மாதிரிகளின் பட்டியல்: $Z(G:\sum _{r\in R}w(r),\sum _{r\in R}(w(r))^{2},\sum _{r\in R}(w(r))^{3},...)$

மாதிரிகளின் எண்ணிக்கை: $Z(G:|R|,|R|,|R|,...)$

நிறுவல்

நிறுவலுக்கென்று தனிக்கட்டுரையைப்பார்க்கவும்

பயன்பாடுகள்

பற்பல பயன்பாடுகள் இருப்பினும் போல்யா தேற்றத்தின் அர்த்தத்தையும் பயன்பாட்டையும் விளக்கக்கூடிய ஒரு சிறு பயன்பாட்டை இங்கு பார்க்கலாம்.

இது ஒரு மாலையின் மணிகளை நிறப்படுத்துதல் என்ற பயன்பாடு.

ஆறு மணிகளைக்கோர்த்த மணிமாலை ஒன்றை பச்சை, சிவப்பு ஆகிய இரண்டு நிறங்களால் நிறப்படுத்தினால் எத்தனை மாதிரி மாலைகள் உண்டுபண்ணலாம்? இதைக் கணக்கிடுவது மட்டுமல்லாமல், போல்யா தேற்றத்தால் அம்மாதிரிகளைப் பட்டியலிடவும் முடியும்.(எண்ணிக்கையைக் கணக்கிடுவது மட்டும் நமது குறிக்கோளானால், அது பர்ன்ஸைட் கொற்கோளாலும் முடியும்).

$D=\{1,2,3,4,5,6\}$ . இவ்வாறு எண்களும் மாலையில் மணிகளின் இடங்களைக் குறிக்கின்றன.

$R$ = பச்சை, சிவப்பு ஆகிய இருநிறங்களால் ஆகிய கணம்.

$f:D\rightarrow R$ என்ற ஒவ்வொரு கோப்பும் ஒருவித நிறப்படுத்தப்பட்ட மாலையைக் குறிக்கும்.

பச்சை நிறத்துக்கு $g$ என்ற 'எடை'யையும், சிவப்பு நிறத்திற்கு $r$ என்ற 'எடை'யையும் கொடுப்போம்.

ஆக $w$(பச்சை) = $g$; $w$(சிவப்பு) = $r$. $g,r$ இரண்டும் ஒரு பரிமாற்று இயற்கணிதத்தின் உறுப்புகள். அதனால் $g+r,g\times r,g^{2},r^{2}$ இதற்கெல்லாம் அர்த்தம் உண்டு.

$D$ இனுடைய ஒரு வரிசைமாற்றுக்குலமாக அதன் சுழற்குலத்தை எடுத்துக்கொள்வோம். அதாவது மாலையை சுழற்றுவதால் ஏற்படும் இடமாற்றங்கள் ஒரு வேறு மாலையாகக் கருதப்படமாட்டாது. எடுத்துக்காட்டாக,

$rgrggg,rgggrg$ இரண்டும் ஒன்றே. (படிமம் பார்க்கவும்).

ஏனென்றால் இரண்டும் ஒரே மாதிரியைச்சேர்ந்தவை. ஒன்றை சரியான அளவு சுழற்றினால் இன்னொன்று கிடைக்கும்.

இச்சுழற்றுக்குலம் என்பது ஆறு உறுப்புக்களால் ஆனது. அந்த ஆறு உறுப்புகளும் அவைகளின் சுழலமைப்புகளும் கீழே அட்டவணையாகக்காட்டப்பட்டுள்ளன:

வரிசைமாற்றம்	சுழலமைப்பு
$(123456)$	${s_{6}}^{1}$
$(135)(246)$	${s_{3}}^{2}$
$(14)(25)(36)$	${s_{2}}^{3}$
$(153)(264)$	${s_{3}}^{2}$
($165432)$	${s_{6}}^{1}$
$(1)(2)(3)(4)(5)(6)$	${s_{1}}^{6}$

இதனால், இச்சுழற்குலத்தின் சுழற்குறியீடு = ${\frac {1}{6}}({s_{1}}^{6}+2{s_{6}}^{1}+2{s_{3}}^{2}+{s_{2}}^{3})$

போல்யா தேற்றத்தின்படி, நிறப்படுத்தப்பட்ட மாலைகளைப் பட்டியலிடுவதற்கு இப்பொழுது நாம் செய்யவேண்டியதெல்லாம், கீழே காட்டியுள்ள பதிலீடுகளை செயல்படுத்தவேண்டும்:

$s_{1}\leftarrow r+g$ (இது 'எடை' களின் கூட்டுத்தொகை, அ-து: $\sum w(r)$ )

$s_{2}\leftarrow r^{2}+g^{2}$ (இது 'எடை' களின் வர்க்கங்களின் கூட்டல், அ-து:$\sum (w(r))^{2}$)

$s_{3}\leftarrow r^{3}+g^{3}$ (இது 'எடை' களின் முப்படியங்களின் கூட்டல், அ-து: $\sum (w(r))^{3}$)

$s_{6}\leftarrow r^{6}+g^{6}$ (இது 'எடை'களின் ஆறாவது அடுக்குகளின் கூட்டல், அ-து $\sum (w(r))^{6}$)

இச்செயல்பாட்டினால் நமக்குக் கிடைப்பது:

${\frac {1}{6}}((r+g)^{6}+2(r^{6}+g^{6})+2(r^{3}+g^{3})^{2}+(r^{2}+g^{2})^{3})$

இதன் கணிப்பு

= $r^{6}+r^{5}g+3r^{4}g^{2}+4r^{3}g^{3}+3r^{2}g^{4}+rg^{5}+g^{6}$

இதன் பொருள்

ஆறு மணிகளும் சிவப்பாக உள்ள மாலை ஒன்று;

ஐந்து மணிகள் சிவப்பாகவும், ஒரு மணி பச்சையாகவும் உள்ள மாலை ஒன்று;

நான்கு மணிகள் சிவப்பாகவும், இரண்டு மணிகள் பச்சையாகவும் உள்ள மாலை மாதிரிகள் மூன்று;

மூன்று மணிகள் சிவப்பாகவும், மூன்று மணிகள் பச்சையாகவும் உள்ள மாலை மாதிரிகள் நான்கு;

இரண்டு மணிகள் சிவப்பாகவும், நான்கு மணிகள் பச்சையாகவும் உள்ள மாலை மாதிரிகள் மூன்று;

ஒரு மணி சிவப்பாகவும், ஐந்து மணிகள் பச்சையாகவும் உள்ள மாலை ஒன்று;

ஆறு மணிகளும் பச்சையாக உள்ள மாலை ஒன்று.

ஆக, 14 மாதிரிகள் உண்டு.

மாதிரிகளின் எண்ணிக்கை மட்டும் தேவையானால், போல்யா தேற்றத்தின் கடைசி பாகத்தில் சொல்லிய வாய்பாடைப் பயன்படுத்தலாம்:

மாதிரிகளின் எண்ணிக்கை = $Z(G:|R|,|R|,...).$ இங்கு |R| = 2.

ஆக, மாதிரிகளின் எண்ணிக்கை = ${\frac {1}{6}}(2^{6}+2\times 2+2\times 2^{2}+2^{3})=14.$

எண்ணல் வரிசைமாற்றுக் குலத்தைப் பொருத்தது

மேலே விவரிக்கப்பட்ட எடுத்துக்காட்டில் வரிசைமாற்றங்களாக மாலையின் 6 சுழற்சிகளை மாத்திரம் எடுத்துக்கொண்டோம். சுழற்சிகளுடன் கூட எதிர்வுகளையும் (reflections) எடுத்துக்கொண்டால், தனித்துவப்படுத்தப்பட்ட மாலைகளின் மாதிரிகளின் எண்ணிக்கை மாறும்.

ஆக, இப்பொழுது எடுத்துக்கொள்ளப்படும் வரிசைமாற்றுக்குலம் G இல்

• ஏற்கனவே எடுத்துக்கொண்ட 6 சுழற்சிகள்;
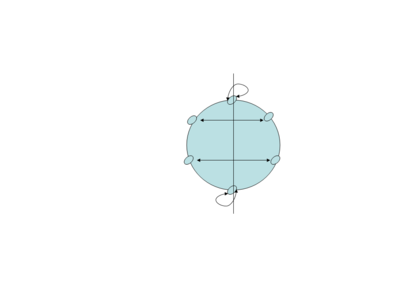
• எதிரெதிர் மணிகளைச்சேர்க்கும் விட்டங்களில் எதிர்வுகள் 3;
• இருமணிகளின் இடைப்புள்ளிகளைச்சேர்க்கும் விட்டங்களில் எதிர்வுகள் 3.

முதலில், இவை பன்னிரண்டும் சேர்ந்து ஒரு குலமாகின்றது என்பது முக்கியம். இக்குலத்தின் சுழற்குறியீட்டைக்கணிக்கும் வழி:

• 6 சுழற்சிகளின் சுழலமைப்புகளின் தொகை (முன் போல்): ${s_{1}}^{6}+2{s_{6}}^{1}+2{s_{3}}^{2}+{s_{2}}^{3}$

• முதல் 3 எதிர்வுகளின் சுழலமைப்புகளின் தொகை: $3{s_{1}}^{2}{s_{2}}^{2}$ (ஒவ்வொரு எதிர்வுக்கும் இரு 2-சுழல்களும் இரு 1-சுழல்களும்)

• இரண்டாவது 3 எதிர்வுகளின் சுழலமைப்புகளின் தொகை: $3s_{2}^{3}$ (ஒவ்வொரு எதிர்வுக்கும் மூன்று 2-சுழல்கள்)

ஆக G இன் சுழற்குறியீடு = ${\frac {1}{12}}({s_{1}}^{6}+2{s_{6}}^{1}+2{s_{3}}^{2}+4{s_{2}}^{3}+3{s_{1}}^{2}{s_{2}}^{2})$

மாதிரிகளின் எண்ணிக்கை = ${\frac {1}{12}}(2^{6}+2.2+2.2^{2}+4.2^{3}+3.2^{2}.2^{2})=13$

ஏற்கனவே கிடைத்த மாதிரிகளின் படிமங்களைப் பார்த்தால், கடைசி இரண்டு மாதிரிகளும், எதிர்வுகளினால் ஒரேமாதிரியாகக் கணக்கிடப்படும் என்பது புரியும். இதர 13 மாதிரிகள்தான் சுழற்சிகளாலும், எதிர்வுகளாலும் மாறாத மாதிரிகள்.