கூம்பி (வளைவரை)

ஒரு வளைவரையின் கூம்பி அல்லது உட்சுருள்வரை (involute) என்பது சிறுசில்லி வகையைச் சேர்ந்த மற்றொரு வளைவரை ஆகும். இதில் உருவாக்கும் புள்ளியைத் தன் மேல்கொண்ட ஒரு கோடு உருளும் வளைவரையாக இருக்கும்.

கூம்பி உருவாக்கப்படும் முறை:

தரப்பட்ட வளைவரை மேல் ஒரு புள்ளியைத் தேர்ந்தெடுத்துக் கொண்டு அப்புள்ளியில் ஒரு கயிற்ற்றின் ஒரு முனையை இணைக்க வேண்டும். பின் கயிற்றின் மறுமுனையைக் கயிறு தொய்வில்லாமல் இருக்குமாறு பிடித்துக் கொண்டபடியே வளைவரையின் மீது சுற்ற, கயிற்றின் மறுமுனையின் பாதையை வரைந்தோமானால் கிடைக்கும் வளைவரை தரப்பட்ட வளைவரையின் கூம்பியாகும்.

கூம்பியாக அமையும் வளைவரைக்கு முதலில் எடுத்துக்கொள்ளப்பட்ட வளைவரை மலரி எனப்படும். (Media:Evolute2.gif, Media:Involute.gif)

கூம்பியை வரையும் முறையில் கயிற்றுக்குப் பதிலாக வளைவரைக்குத் தொடுகோடாக இருக்கும் ஒரு கோட்டுத்துண்டை எடுத்துக் கொள்ளலாம். இக்கோட்டுத்துண்டின் ஒரு முனை வளைவரையின் மீது தொடுபுள்ளியாக இருக்கும். மற்றொரு முனையின் பாதை கூம்பியாக அமையும். இம்முறையில் தொடுபுள்ளி வளைவரை மீது நகரும் வில்லின் நீளத்தின் அளவில் தொடுகோட்டின் நீளம் மாறும்.

துணையலகுச் சமன்பாடுகள்

$X[x,y]=x-\frac{x'\int_a^t \sqrt { x'^2 + y'^2 }\, dt}{\sqrt { x'^2 + y'^2 }}$

$Y[x,y]=y-\frac{y'\int_a^t \sqrt { x'^2 + y'^2 }\, dt}{\sqrt { x'^2 + y'^2 }}$

எடுத்துக்காட்டுகள்

ஒரு வட்டத்தின் கூம்பி

ஒரு வட்டத்தின் கூம்பி

ஒரு வட்டத்தின் கூம்பியின் வடிவம் ஆர்க்கிமிடியச் சுருள் போல இருக்கும்.

• கார்ட்டீசியன் ஆள்கூறுகளில் வட்டத்தின் கூம்பியின் துணையலகுச் சமன்பாடுகள்:

$\, x = a \left( \cos\ t + t\sin\ t \right)$

$\, y = a \left( \sin\ t - t\cos\ t \right)$

இங்கு $\, a,$ வட்டத்தின் ஆரம். $\, t,$ ரேடியனில் கோணத் துணையலகு ($\ t \in \mathbb{R}$).

• போலார் ஆள்கூறுகளில் $\, r,\varphi$ வட்டத்தின் கூம்பியின் துணையலகுச் சமன்பாடுகள்:

$\, r=a\cdot\sec\alpha=\frac{a}{\cos\alpha}$

$\, \varphi = \tan\alpha - \alpha$

இங்கு $\, a$ வட்டத்தின் ஆரம். $\ -\pi/2<\alpha<\pi/2$ இடைவெளியில் அமையும் துணையலகு $\, \alpha.$

$\ \tau\ (\$ $\ \tau=\tan\alpha\ ;\ \tau\in \mathbb{R}\ )$ என்ற துணையலகில் இதன் சமன்பாடுகள்:

$\, r = a\cdot \sqrt{1+\tau^2}$

$\, \varphi=\tau-\arctan(\tau)$.

வில்லின் நீளம்

வட்டத்தின் கூம்பியின் வில்லின் நீளம்:

$\ L = \frac{a}{2}\cdot t_1^2,$ $\ (\quad0\le t\le t_1\quad)$

பயன்பாடு

பற்சக்கரத் துணைப்பொறியின் பற்களை வடிவமைப்பதில் வட்டத்தின் கூம்பி வடிவம் ஆய்லரால் பரிந்துரைக்கப்பட்டது. இன்றும் இவ்வடிவம் உள்சுருள்வரை பல்சக்கர அமைப்பில் பயன்பாட்டில் உள்ளது.

சங்கிலியத்தின் கூம்பி

சங்கிலியத்தின் கூம்பி.

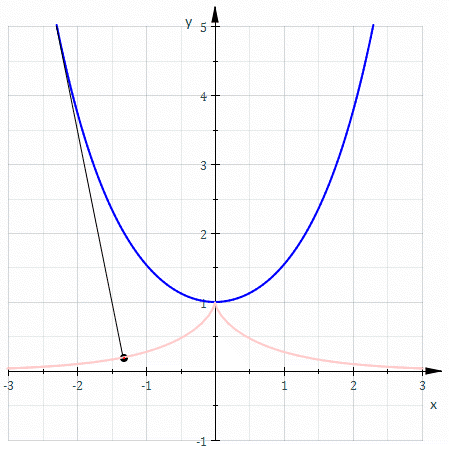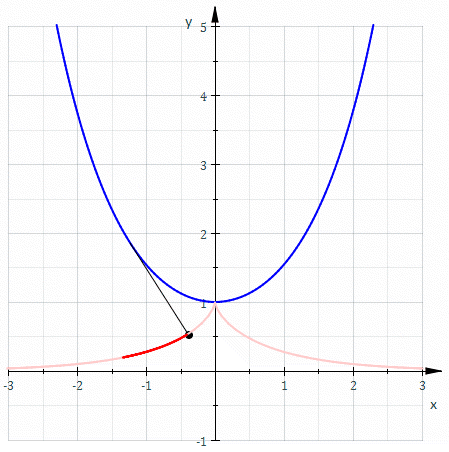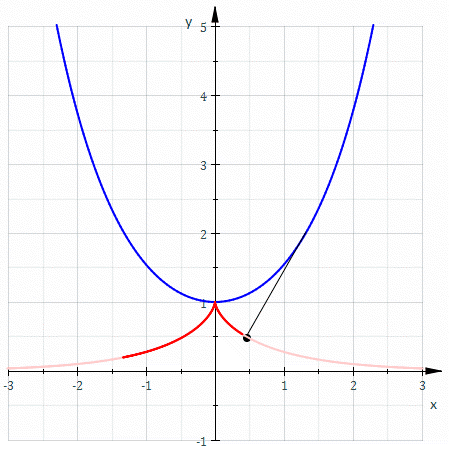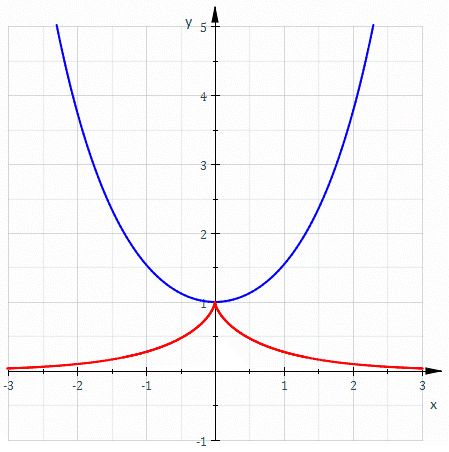
சங்கிலியத்தின் உச்சி வழியே அமையும் அதன் கூம்பி ஒரு (tractrix).

கார்ட்டீசியன் ஆள்கூறுகளில் அதன் சமன்பாடு:

$x=t-\mathrm{tanh}(t)\,$

$y=\mathrm{sech}(t)\ =\ \frac{1}{\mathrm{cosh}(t)}$

இங்கு t என்பது துணையலகு.

வட்டப்புள்ளியுருவின் கூம்பி

ஒரு வட்டப்புள்ளியுருவும் அதன் கூம்பியும் ஒன்றுக்கொன்று வடிவொத்தவை.

வெளி இணைப்புகள்

• Mathworld