விண்மீன் கோட்டுரு
| விண்மீன் | |
|---|---|
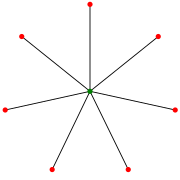 விண்மீன் S7. (சிலர் இதனை S8 என்றும் குறிப்பதுண்டு.) | |
| முனைகள் | k+1 |
| விளிம்பு | k |
| விட்டம் | (2, k) இன் சிறுமவளவு |
| சுற்றளவு | ∞ |
| நிற எண் | (2, k + 1) இன் சிறுமவளவு |
| நிறச் சுட்டெண் | k |
| இயல்புகள் | விளிம்புக்-கடப்பு மரம் அலகு தொலைவு இருகூறானது |
| Notation | Sk |
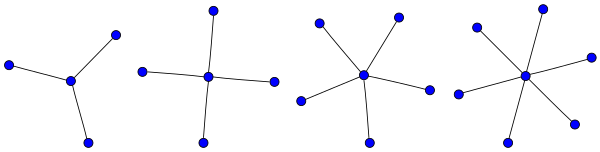
கோட்டுருவியலில் விண்மீன் அல்லது விண்மீன் கோட்டுரு (star) Sk என்பது முழு இருகூறு கோட்டுருவாகும். இக்கோட்டுரு ஒரு உள்முனையும் k இலைகளும் கொண்ட மரமாக (K1,k) இருக்கும். k ≤ 1 எனில் இம்மரத்தில் உள்முனை இருக்காது, k + 1 இலைகள் இருக்கும்).
மாறாக, சில நூலாசிரியர்கள் விண்மீனை (Sk) அதிகபட்சம் 2 அலகு விட்டமும் k வரிசையும் கொண்ட மரமாக வரையறுக்கின்றனர். இந்த வகையில் k > 2 எனில் அந்த விண்மீனில் k − 1 இலைகள் இருக்கும்
ஒன்றுக்கும் அதிகமான படிகொண்ட அதிகபட்ச முனைகள் ஒன்று மட்டுமேயுள்ள இணைப்புள்ள கோட்டுருக்களாகவும் விண்மீன் கோட்டுருக்களை வரையறுக்கலாம்.
கவ்வி
[தொகு]
மூன்று படியுடைய விண்மீன் கவ்வியென (claw) அழைக்கப்படுகிறது.
கவ்வியற்றக் கோட்டுருக்களின் வரையறையில் கவ்விகள் குறிப்பிடத்தக்கவை. கவ்வியற்ற கோட்டுருக்களின் எந்தவொரு தூண்டப்பட்ட உட்கோட்டுருவும் கவ்வியாக இருக்காது.[1][2]
பயன்பாடுகள்
[தொகு]பல கோட்டுரு பண்புகள் விண்மீன்களைக் கொண்டு வரையறுக்கப்பட்டுள்ளன:
- ஒரு கோட்டுருவைக் காடுகளாகப் பிரிக்கும்போது அக்காடுகளிலுள்ள ஒவ்வொரு மரமும் ஒரு விண்மீனாக இருக்கவேண்டும் என்ற கட்டுப்பாட்டுக்குட்பட்டு பிரிக்கப்படக்கூடிய காடுகளின் என்ணிக்கையின் சிறுமமதிப்பு விண்மீன் எண்ணிக்கை (Star arboricity) எனப்படும்.[3]
- ஒரு கோட்டுருவின் "விண்மீன் நிற எண்" என்பது "ஒவ்வொரு இரண்டு நிறத் தொகுதிகள் இணைந்து உருவாக்கும் உட்கோட்டுருக்களின் இணைப்புள்ள கூறுகள் அனைத்தும் விண்மீன்களாக இருக்க வேண்டும்" என்பதற்குட்பட்டு அக்கோட்டுருவின் முனைகளை நிறந்தீட்டத் தேவைப்படும் நிறங்களின் எண்ணிக்கையின் சிறுமவளவு ஆகும்.[4]
- கிளை அகலம் 1 உடைய கோட்டுருக்களின் ஒவ்வொரு இணைப்புள்ள கூறுகளும் ஒரு விண்மீனாக இருக்கும்.[5]
இதர பயன்பாடுகள்
[தொகு]- ஒரு கவ்வியின் முனைகளுக்கு இடைப்பட்ட தொலைவுகளின் கணம், சமவளவை உருமாற்றத்தால் எப்பரிமாண யூக்ளிடிய வெளிக்குள்ளும் உட்பொதிய முடியாத ஒரு முடிவுறு மெட்ரிக் வெளிக்கு எடுத்துக்காட்டாக அமைகிறது.[6]
- விண்மீன் கோட்டுருவை மாதிரியாகக் கொண்ட கணினி வலையமைப்பான விண்மீன் வலையமைப்பு, விரவல் கணினி செய்முறையில் முக்கியமான ஒன்றாகும்.
மேற்கோள்கள்
[தொகு]- ↑ Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), "Claw-free graphs — A survey", Discrete Mathematics, 164 (1–3): 87–147, எண்ணிம ஆவணச் சுட்டி:10.1016/S0012-365X(96)00045-3, MR 1432221.
- ↑ Chudnovsky, Maria; Seymour, Paul (2005), "The structure of claw-free graphs", Surveys in combinatorics 2005 (PDF), London Math. Soc. Lecture Note Ser., vol. 327, Cambridge: Cambridge Univ. Press, pp. 153–171, MR 2187738.
- ↑ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. E. (1996), "Star arboricity of graphs", Discrete Math., 149: 93–98, எண்ணிம ஆவணச் சுட்டி:10.1016/0012-365X(94)00313-8
- ↑ Fertin, Guillaume; Raspaud, André; Reed, Bruce (2004), "Star coloring of graphs", Journal of Graph Theory, 47 (3): 163–182, எண்ணிம ஆவணச் சுட்டி:10.1002/jgt.20029.
- ↑ Robertson, Neil; Seymour, Paul D. (1991), "Graph minors. X. Obstructions to tree-decomposition", Journal of Combinatorial Theory, 52 (2): 153–190, எண்ணிம ஆவணச் சுட்டி:10.1016/0095-8956(91)90061-N.
- ↑ Linial, Nathan (2002), "Finite metric spaces–combinatorics, geometry and algorithms", Proc. International Congress of Mathematicians, Beijing, vol. 3, pp. 573–586, arXiv:math/0304466, Bibcode:2003math......4466L

