திசைவேகம்
 | |
| பொதுவான குறியீடு(கள்): | v, v |
| SI அலகு: | m/s |
திசைவேகம் அல்லது விரைவு (velocity) என்பது ஒரு பொருளின் குறிப்பிட்ட திசையில் நிகழும் இடப்பெயர்ச்சி வீதம் ஆகும். குறிப்பிட்ட நேர அலகுக்கு (எடுத்துக்காட்டாக ஒரு நொடிக்கு) ஒருதிசையில் ஒரு பொருள் எவ்வளவு தொலைவுக்கு இடம்பெயர்கிறது என்பது திசைவேகம் ஆகும். திசைவேகமானது அதன் பருமையாலும், இயங்கும் திசையாலும் குறிப்பிடப்படுகிறது (எ.கா: வடக்கு நோக்கி 60 கி.மீ./மணி (km/hr)). பொருள்களின் இயக்கத்தை விவரிக்கும் செவ்வியல் இயக்கவியலின் ஒரு கிளைப்பிரிவாகிய இயக்கவடிவியலில், திசைவேகம் என்பது ஓர் அடிப்படையான முதன்மை வாய்ந்த கருத்துரு ஆகும்.
திசைவேகம் என்பது இயற்பியல் நெறிய (திசையன்) அளவாகும். இதனை வரையறுக்க அதன் பருமையும் (magnitude), திசையும் வேண்டும். திசைவேகத்தின் பருமை வேகம் (speed) ஆகும். திசைவேகமும், வேகமும் ஒருங்கியைவான கொணர்வு அலகைப் பெற்றுள்ளன. இவற்றின் அளவு பன்னாட்டுச் செந்தர அலகு முறையில் (மெட்ரிக் முறை) மீட்டர்/நொடி (m/s) யால் அளக்கப்படுகிறது. இதன் பசெ (SI) அடிப்படை அலகு m⋅s−1 ஆகும். எடுத்துகாட்டாக, "5 மீட்டர்கள்/ நொடி" என்பது அளவன் ஆகும்; ஆனால், "5 மிட்டர்கள்/நொடி கிழக்கில்" என்பது நெறியன் ஆகும்.
ஒரு பொருளின் வேகத்திலோ, திசையிலோ அல்லது இரண்டிலுமோ மாற்றம் நிலவினால், அப்போது அப்பொருளின் திசைவேகம் மாறுவதாகவும், முடுக்கமுறுவதாகவும் கூறப்படும். திசைவேகத்தின் மாறுகின்ற வீதம் முடுக்கம் ஆகும். முடுக்கம் ஒரு பொருளின் திசைவேகம் காலத்தை பொறுத்து மாறும் வீதத்தைக் குறிக்கும்.
நிலைத்த திசைவேகமும், முடுக்கமும்
[தொகு]நிலைத்த திசைவேகம்
[தொகு]ஒரு குறிப்பிட்ட திசையில் ஒரு பொருள் இயங்கும் போது, கால இடைவெளிகள் மிகச் சிறியதாக இருப்பினும், சமகால இடைவெளிகளில் சம இடப்பெயர்ச்சியைக் கடந்தால், அப்பொருள் நிலையான திசைவேகத்தில் இயங்குகிறது எனலாம்.
நிலையான திசைவேகத்தில் இயங்குவதற்கு, ஒரு பொருள் நிலையான வேகத்தில் நிலைத்த திசையில் செல்லவேண்டும். நிலையான திசை பொருளை நேர்க்கோட்டில் மட்டுமே செல்லவிடும். எனவே நிலையான திசைவேகம் என்பது நேர்க்கோட்டில் அமையும் நிலைத்த வேக இயக்கத்தைக் குறிப்பிடும்.
முடுக்கம்
[தொகு]ஒரு பொருள் இயங்கும் போது கால இடைவெளிகள் மிகச் சிறியதாக இருப்பினும், சமகால இடைவெளிகளில் மாறுபட்ட இடப்பெயர்ச்சியை மேற்கொண்டாலோ அல்லது அதன் திசையில் மாற்றமிருந்தாலோ அல்லது இரண்டிலுமே மாற்றம் நிகழ்ந்தாலோ, பொருள் முடுக்கத்தில் இயங்குகிறது எனலாம். எடுத்துகாட்டாக, ஒரு சீருந்து வட்டத்தில் நிலையாக மணிக்கு 20 கிமீ இயங்கினால் அது நிலையான வேகத்தில் செல்வதாகக் கூறப்படும். ஆனால், அதன் திசை மாறுவதால் நிலையான திசைவேகத்தில் இயங்குவதாகக் கூற முடியாது. எனவே, சீருந்து முடுக்கம் அடைவதாகக் கூறப்படும்.
வேகம், திசைவேகம் வேறுபாடு
[தொகு]
வேகம் என்பது எவ்வளவு விரைவாக ஒரு பொருள் இடப்பெயர்ச்சி அடைகிறது என்பதையும், திசைவேகம் என்பது எவ்வளவு விரைவாக, எந்த திசை நோக்கி ஒரு பொருள் நகருகிறது என்பதையும் குறிப்பதாகும்.[1] ஒருசீருந்து 60 கிமீ/ம வேகத்தில் இயங்கிக் கொண்டிருக்கிறது என்றால், அதன் வேகம் மட்டுமே குறிப்பிடப்படுகிறது. ஆனால், ஒருசீருந்து 60 கிமீ/ம வேகத்தில் கிழக்கு நோக்கி இயங்கிக் கொண்டிருக்கிறது என்று குறிப்பிட்டால், அதன் திசைவேகம் குறிப்பிடப்படுகிறது.
வட்டத்தில் நிகழும் இயக்கத்தைக் கருதுவோமானால், இவற்றுக்கு இடையில் உள்ள பெரிய வேறுபாட்டைக் காணலாம். வட்ட வழித்தடத்தில் ஒரு பொருள் நிலையான வேகத்தில் இயங்கி, அது தன் தொடக்கப் புள்ளிக்கே திரும்பினால், அதன் சராசரி திசைவேகம் சுழியம் அல்லது பூச்சியம் ஆகும். ஆனால் அதன் சராசரி வேகம், வட்டப் பரிதியை அது வட்டத்தைச் சுற்ற எடுத்துக்கொண்ட நேரத்தால் வகுத்தால் கிடைக்கும் மதிப்பாகும். சராசரி திசைவேகம் தொடக்கப் புள்ளியிலும் முடிவுப் புள்ளியிலும் உள்ள இடப்பெயர்ச்சி நெறியங்களைக் கருதிக் கணக்கிடப்படுவதால் இந்நிலை உருவாகிறது. ஆனால் சராசரி வேகமோ மொத்தப் பயணத் தொலைவையும் கருதுகிறது.
இயக்கச் சமன்பாடு
[தொகு]சராசரி திசைவேகம்
[தொகு]திசைவேகம் நேரத்தைப் பொறுத்த இருப்பு மாற்ற வீதம் என வரையறுக்கப்படுகிறது. இதைச் சராசரி திசைவேகத்தில் இருந்து வேறுபடுத்த, கணத் திசைவேகம் எனவும் கூறலாம். சில பயன்பாடுகளில் சராசரி திசைவேகம் கட்டாயமாகத் தேவைப்படுகிறது. அதாவது, குறிப்பிட்ட நேர இடைவெளியில் மாறும் திசைவேகத்துக்குச் சமமான இடப்பெயர்ச்சியைத் தரவல்ல, சமச் சராசரி திசைவேகம் தேவைப்படும். அதாவது, Δt கால இடைவெளியில் v(t), தேவைப்படுகிறது . அச்சராசரி திசைவேகத்தைப் பின்வருமாறு கணக்கிடலாம்:
ஒரு பொருளின் சராசரி திசைவேகம், அதன் சராசரி வேகத்துக்குக் குறைவாகவோ சமமாகவோ இருக்கும். தொலைவு தொடர்ந்து கூடிக்கொண்டே போனாலும், இடப்பெயர்ச்சி நெறியம் அளவில் கூடவோ குறையவோ செய்வதோடு திசையிலும் மாறலாம் என்பதைக் கருதினால், மேற்கூறிய உண்மையை புரிந்து கொள்ளலாம். (x vs. t) எனும் இடப்பெயர்ச்சி-நேர வரைபடத்தில் இருந்து, கணத் திசைவேகத்தை (அல்லது, வெறுமனே, திசைவேகத்தை) அப்படத்தின் ஏதாவது ஒரு புள்ளியில் அமையும் தொடுகோட்டின் சரிவாகக் கருதலாம்; அதேபோல, சராசரி திசைவேகத்தை அதன் கால இடைவெளியின் இருபுறமும் அமையும் இருபுள்ளிகளின் ஆயங்களுக்கு இடையில் உள்ள தொடுகோட்டைக் குத்தும் செங்குத்தின் சரிவாகக் கருதலாம்.
சராசரி திசைவேகம் என்பது திசைவேகத்தின் காலச் சராசரி மதிப்பாகும்; அதாவது, கால இடைவெளியில் சராசரியாக அமையும் திசைவேகம் ஆகும். இதைப் பின்வருமாறு கணக்கிடலாம்:
இங்கு,: ஆகும்.மேலும்
- ஆகும்.
கணத் திசைவேகம்
[தொகு]ஒரு பொருள் கடக்கும் வழித்தடத்தில் ஏதேனும் ஒரு புள்ளியில் அல்லது குறிப்பிட்ட கணத்தில் ஏற்படும் மாற்றம் கணத் திசைவேகம் எனப்படும்.
நாம் v ஐத் திசைவேகமாகவும் x ஐ இடப்பெயர்ச்சி நெறியமாகவும் (இருப்பு மாற்றமாகவும்) கருதினால், அப்போது ஒரு புள்ளி அல்லது பொருளின் குறிப்பிட்ட t நேரத்தில் உள்ள கணத் திசைவேகத்தை, இருப்பின் நேரம் சார்ந்த வகைக்கெழுவாக பின்வருமாறு கோவைப்படுத்தலாம்:
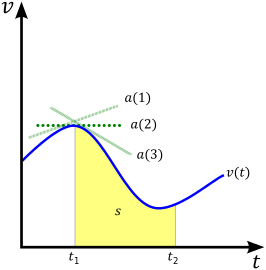
ஒருபருமானத்தில் அமைந்த இந்த வகைக்கெழு சமன்பாட்டில் இருந்து, திசைவேகம்-நேர (v vs. t வரைபடத்தில்), x எனும் இடப்பெயர்ச்சி அமைதலைக் காணலாம்; நுண்கலனக் கணிதப்படி, v(t)எனும் திசைவேகச் சார்பின் தொகையமாக x(t) எனும் இடப்பெயர்ச்சி சார்பு அமைதலைக் காணலாம். வரைபடத்தில், s என்பது (s எனப் பெயரிட்டு, வரைவின் கீழமைந்த மஞ்சட் பரப்புக்கான), இடப்பெயர்ச்சிக்கான மாற்றுக் குறிமானமாக அமைகிறது).
நேரத்தைப் பொறுத்த இருப்பின் வகைக்கெழு, மீட்டர்களில் உள்ள இருப்பை நொடிகளில் அமையும் நேர மாற்றத்தால் வகுத்துப் பெறுவதால், திசைவேகமானது மீட்டர்கள்/நொடி (m/s) எனும் அலகால் அளக்கப்படுகிறது. கணத் திசைவேகம் எனும் கருத்துப்படிமம் முதலில் உய்த்துணரவியலாததாகத் தோன்றினாலும், அதை அக்கணத்தில் முடுக்கம் இல்லாமல் தொடர்ந்து செல்லும் பொருளின் வேகமாகக் கொள்ளலாம்.
திசைவேக, முடுக்க உறவு
[தொகு]திசைவேகத்தை இருப்பு மாற்ற வீதமாக வரையறுத்தாலும், பொருளின் முடுக்கத்தின் கோவையில் இருந்து தொடங்குவதே வழக்கமாக உள்ளது. படத்தில் உள்ள பச்சைத் தொடுகோடுகள், குறிப்பிட்ட நேரத்தில் உள்ள ஒரு பொருளின் கண முடுக்கங்கள் ஆகும். அப்புள்ளியில் உள்ள v(t) எனும் திசைவேகம் வரைபடத்தில் உள்ள வளைவில் அமையும் தொடுகோட்டின் சரிவாகும் . அதாவது முடுக்கம், திசைவேகத்தின் நேரம் சார்ந்த வகைக்கெழுவாக மாற்றுவழியில் பின்வருமாறு வரையறுக்கப்படுகிறது:
இதில் இருந்து, திசைவேகத்துக்கான கோவை v(t) சார்பை முடுக்கம்-நேரம் சார்ந்த வரைபடத்தில் வளைவின் கீழமையும் பரப்பாக கொண்டுவரலாம். மேலுள்ளபடியே, தொகையக் கருத்துப்படிமத்தைப் பயன்படுத்திப் பின்வரும் சமன்பாட்டைப் பெறலாம்:
நிலையான முடுக்கம்
[தொகு]சிறப்பு நேர்வாக நிலைத்த முடுக்கத்தைக் கருதினால், திசைவேகத்தைச் சுவாத் சமன்பாட்டைக் கொண்டு ஆயலாம். a வை ஓர் தற்சார்பான நிலைத்த நெறியமாகக் கொண்டால், பின்வரும் உறவைக் கொணர்வது மிக எளியதே.
இங்கு v என்பது t நேரத்து மதிப்பு; அதேபோல, u என்பது t = 0 நேரத்து மதிப்பு. இந்தச் சமன்பாட்டைச் சுவாத் சமன்பாடு x = ut + at2/2 என்பதோடு இணைத்தால், இடப்பெயர்ச்சியையும் சராசரி திசைவேகத்தையும் பின்வருமாறு உறவுப்படுத்த முடியும்.
- .
நேரம் சாராத திசைவேகத்தின் சார்பை, அதாவது டாரிசில்லி சமன்பாட்டைப் பின்வருமாறு கொணரலாம்:
இங்கு v = v அளவன் ஆகும்.
மேலுள்ள சமன்பாடுகள் நியூட்டனின் இயக்கவியலுக்கும் சிறப்புச் சார்புக் கோட்பாட்டுக்கும் பொருந்தும். ஒரே சூழலைப் பல்வேறு நோக்கீட்டாளர்கள் எப்படி விவரிப்பார்கள் என்பதில் தான் நியுட்டனின் இயக்கவியலும் சிறப்புச் சார்புக் கோட்பாடும் வேறுபடுகின்றன. குறிப்பாக, நியூட்டனின் இயக்கவியலில், அனைத்து நோக்கர்களும் t சார்ந்த மதிப்பை ஏற்பர்; இருப்புக்கான உருமாற்ற விதிகள், முடுக்கமற்ற சட்டக நோக்கர்கள் ஒரு பொருளின் முடுக்கத்தை ஒரே மதிப்பாக விவரிக்கும் சூழலை உருவாக்குகின்றன. இரண்டுமே சிறப்புச் சார்புக் கோட்பாட்டின்படி, உண்மையல்ல. மாறாக, இதன்படி சார்பு விரைவு மட்டுமே அளக்கவியன்றதாகும்.
திசைவேகம் சார்ந்த அளவுகள்
[தொகு]இயங்கும் பொருளின் இயக்க ஆற்றல் திசைவேகத்தைச் சார்ந்ததாகும். அதன் சமன்பாடு பின்வருமாறு
சிறப்புச் சார்புக் கோட்பாட்டை கருதாவிட்டால், Ek என்பது இயக்க ஆற்றல்; m என்பது பொருண்மை. இயக்க ஆற்றல் விரைவின் இருபடி மதிப்பைச் சார்ந்துள்ளதால், இது ஓர் அளவன் ஆகும்; என்றாலும் இதோடு உறவுள்ள உந்தம், ஒரு நெறிய மாகும். உந்தம் பின்வரும் சமன்பாட்டால் வரையறுக்கப்படுகிறது.
சிறப்புச் சார்பியலில், பருமானமற்ற பின்வரும் இலாரன்சு காரணி அடிக்கடி பயன்படுகிறது.
இங்கு, γ என்பது இலாரன்சு காரணி; c என்பது ஒளியின் திசைவேகம் ஆகும்.
விடுபடு திசைவேகம் அல்லது தப்பிப்புத் திசைவேகம் என்பது புவிபோன்ற உயர்பொருண்மைப் பொருளில் இருந்து எறியப்பட்ட பொருள் அதில் இருந்து தப்பித்து வெளியேறுவதற்குத் தேவையான சிறும வேகமாகும். இது பொருளின் இயக்க ஆற்றலை அப்பொருளின் ஈர்ப்பு ஆற்றலோடு (இது எப்போதும் எதிர்மதிப்பில் அமையும்) கூட்டும்போது சுழி மதிப்பை அடையும் நிலையாகும். M பொருண்மையுள்ள கோளின் மையத்தில் இருந்து r தொலைவில் அமைந்த பொருளின் விடுபடு அல்லது தப்பிப்புத் திசைவேகத்துக்கான பொது வாய்பாடு கீழே தரப்படுகிறது.
இங்கு, G என்பது ஈர்ப்பு மாறிலி; g என்பது ஈர்ப்பு முடுக்கம். புவியில் இருந்து தப்பிப்பதற்கான விடுபடு திசைவேகம் 11 200 மீ/நொ ஆகும்; இது பொருளின் திசையைச் சார்ந்து அமைவதில்லை. எனவே இச்சொல் விடுபடு வேகம் என்றமைதலே சரியாகும்:இந்தத் திசைவேகப் பருமையை (அளவை) அடையும் எந்தவொரு பொருளும் அதன் வழித்தடத்தில் வேறு ஏதாவது குறுக்கிட்டால் ஒழிய, எவ்வித வளிமண்டல நிலைமையின் கீழும், தன்னை ஈர்க்கும் முதற்பொருளில் இருந்து விடுபட்டு வெளியேறும்.
குறிப்புகள்
[தொகு]- ↑ Wilson, Edwin Bidwell (1901). Vector analysis: a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. p. 125. This is the likely origin of the speed/velocity terminology in vector physics.
மேற்கோள்கள்
[தொகு]- Robert Resnick and Jearl Walker, Fundamentals of Physics, Wiley; 7 Sub edition (June 16, 2004). பன்னாட்டுத் தரப்புத்தக எண் 0-471-23231-9.
வெளி இணைப்புகள்
[தொகு]- physicsabout.com, Speed and Velocity
- Velocity and Acceleration
- Introduction to Mechanisms (கார்னிகி மெல்லன் பல்கலைக்கழகம்)


















