ஈரோனிய சராசரி

கணிதத்தில் இரு எதிர்மமற்ற மெய்யெண்கள் A , B இன் ஈரோனிய சராசரி (Heronian mean) H ஆனது பின்வரும் வாய்பாட்டால் தரப்படுகிறது:

$H={\frac {1}{3}}\left(A+{\sqrt {AB}}+B\right).$

இச்சராசரி, கணிதவியலாளர் ஈரோனின் பெயரால் அறியப்படுகிறது.

திண்ம வடிவவியலில் பயன்பாடு

சதுர அடிக்கண்டம். இந்த அடிக்கண்டத்தின் கனவளவானது, அதன் உயரம் மற்றும் எதிரெதிர் சதுர அடிப்பக்கங்களின் பரப்பளவுகளின் ஈரோனின் சராசரியின் பெருக்குத்தொகை.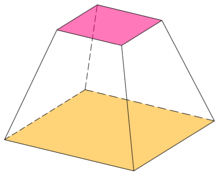

திண்ம வடிவவியலில் ஒரு கூம்பு அல்லது பட்டைக்கூம்பின் அடிக்கண்டத்தின் கனவளவைக் கணக்கிடுவதற்குப் பயன்படுகிறது. அடிக்கண்டத்தின் கனவளவானது, அதன் உயரம் மற்றும் எதிரெதிர் இணை அடிப்பக்கங்களின் பரப்பளவுகளின் ஈரோனின் சராசரியின் பெருக்குத்தொகையாகும்.

$V={\frac {h}{3}}\left(B_{1}+{\sqrt {B_{1}B_{2}}}+B_{2}\right)$.

பிற சராசரிகளுடான தொடர்பு

A , B இரண்டின் ஈரோனிய சராசரியானது இவ்விரு எண்களின் கூட்டு மற்றும் பெருக்கல் சராசரிகளின் எடையிடப்பட்ட சராசரியாகும்:

$H={\frac {2}{3}}\cdot {\frac {A+B}{2}}+{\frac {1}{3}}\cdot {\sqrt {AB}}.$

மேற்கோள்கள்

• Bullen, P.S. (2003), Handbook of Means and Their Inequalities, Mathematics and Its Applications (2nd ed.), Berlin, New York: இசுபிரிங்கர் பதிப்பகம், பன்னாட்டுத் தரப்புத்தக எண் 978-1-4020-1522-9
• Eves, Howard Whitley (1980), Great Moments in Mathematics (Before 1650), அமெரிக்கக் கணிதவியல் சங்கம், பன்னாட்டுத் தரப்புத்தக எண் 978-0-88385-310-8

வெளியிணைப்புகள்

• Mean-Trapezoids Geometric comparison of some mathematical means