அடிக்கண்டம்
| பட்டைக்கூம்பு அடிக்கண்டங்கள் | |
|---|---|
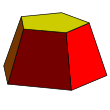  ஐங்கோண, சதுர அடிக்கண்டம் | |
| முகம் | n சரிவகங்கள், 2 n-கோணிகள் |
| விளிம்பு | 3n |
| உச்சி | 2n |
| சீரொருமைக் குழு | Cnv, [1,n], (*nn) |
| பண்புகள் | குவிவு |
வடிவவியலில் அடிக்கண்டம் (frustum[a]) என்பது, திண்மத்தில் ஒன்று அல்லது இரண்டு இணையான தளங்களுக்கு இடையே அமையும் ஒரு பகுதியாகும். பொதுவாக, இத்திண்மம் கூம்பு அல்லது பட்டைக்கூம்பாக இருக்கும். ஒரு நேர் பட்டைக்கூம்பு அல்லது கூம்பை இணையான முனைத்துண்டிப்புச் செய்யக் கிடைக்கும் அடிக்கண்டமானது, நேர் அடிக்கண்டம் (right frustum) எனப்படும்.[3]
தொடர்புள்ள கூறுகள்[தொகு]
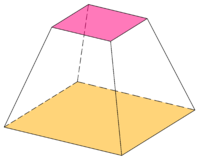

ஒரு அடிக்கண்டத்தின் அச்சானது, அதன் மூலத்திண்மத்தின் (கூம்பு அல்லது பட்டைக்கூம்பு) அச்சாகவே இருக்கும். வட்ட அடிப்பக்கங்கொண்ட அடிக்கண்டங்கள் வட்டமாக இருக்கும். அடிக்கண்டத்தின் அச்சு, அதன் இரு அடிப்பக்கங்களுக்கும் செங்குத்தாக இருந்தால் அது "நேர் அடிக்கண்டமாக" இருக்கும். இல்லையெனில், அது "சாய்வு அடிக்கண்டமாக" இருக்கும்.
அடிக்கண்டத்தின் இரு அடிகளுக்கும் இடைப்பட்டச் செங்குத்து தூரம், அந்த அடிக்கண்டத்தின் உயரமாகும்.
இரு அடிக்கண்டங்களை அவற்றின் அடிப்பக்கத்தில் இணைத்தால் இருஅடிக்கண்டம் கிடைக்கும்.
கனவளவு[தொகு]
சதுரப் பட்டைக்கூம்பின் அடிக்கண்டத்தின் கனவளவிற்கான வாய்பாடு பண்டைய எகிப்திய கணிதத்தில் அறிமுகப்படுத்தப்பட்டது. இது, எகிப்தின் பதிமூன்றாம் வம்ச காலத்தில் எழுதப்பட்ட (அண். 1850 BC) "மாஸ்கோ கணித பாபிரசி"ல் உள்ளது:
இதில், a, b இரண்டும் அடிக்கண்டத்தின் அடி மற்றும் மேற்பக்க நீளங்கள்; h, உயரம். எகிப்தியர்கள் சதுரப் பட்டைக்கூம்பு அடிக்கண்டத்தின் கனவளவின் சரியான வாய்பாட்டினை அறிந்திருந்தாலும் அதற்கான நிறுவல் மாஸ்கோ பாபிரசில் காணப்படவில்லை.
கூம்பு அல்லது பட்டைக்கூம்பின் அடிக்கண்டத்தின் கன அளவு, நுனி துண்டிக்கப்படாத முழுத்திண்மத்தின் கனவளவிலிருந்து துண்டிக்கப்பட்ட நுனிப்பகுதியின் கனவளவைக் கழிக்கக் கிடைக்கும்:
B1 - அடிக்கண்டத்தின் ஒரு அடிப்பக்கத்தின் பரப்பளவு; B2 - அடிக்கண்டத்தின் மற்றொரு அடிப்பக்கத்தின் பரப்பளவு; h1, h2 இரண்டிம் மேலுச்சியிலிருந்து இரு அடிப்பக்கத் தளங்களுக்கான உயரங்கள்.
- என எடுத்துக்கொண்டால் அடிக்கண்டத்தின் கனவளவிற்கான வாய்பாடு:
a3 − b3 = (a − b)(a2 + ab + b2) என்ற முற்றொருமையைப் பயன்படுத்த:
h1 − h2 = h, α இன் மதிப்பை மேலுள்ள வாய்பாட்டில் பதிலிடக் கிடைக்கும் கனவளவின் வாய்பாடு:
- .
- - இது பரப்பளவுகள் B1, B2 ஆகிய இரண்டின் ஈரோனிய சராசரி ஆகும்.
கற்பனை அலகுடன் அமைந்த இந்த அடிக்கண்டத்தின் கனவளவு வாய்பாட்டிற்காக கணிதவியலாலர் அலெக்சாந்திரியாவின் ஹீரோன் நன்கறியப்பட்டார்.[4]
வட்டக்கூம்பு அடிக்கண்டத்தின் கனவளவு:
இதில், r1, r2 இரண்டும் அடிக்கண்டத்தின் இரு வட்ட அடிப்பக்கங்களின் ஆரங்கள்.

n-பக்க ஒழுங்கு பல்கோண அடிப்பக்கங்களைக் கொண்ட பட்டைக்கூம்பு அடிக்கண்டத்தின் கனவளவு:
இதில் a1, a2 அடிக்கண்டத்தின் இரு அடிப்பக்கங்களின் பக்க அளவுகள்.
புறப்பரப்பளவு[தொகு]
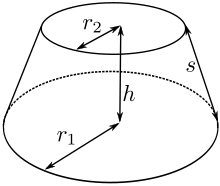

ஒரு நேர்வட்டக் கூம்பு அடிக்கண்டத்திற்கு:[5][6]
இதில் r1, r2 இரண்டும் அடிக்கண்டத்தின் இரு அடிப்பக்க வட்டங்களின் ஆரங்கள்; s - அடிக்கண்டத்தின் சாய்வு உயரம்.
வடிவொத்த n-பக்க ஒழுங்கு பல்கோணிங்களை அடிகளாகக் கொண்ட நேர் அடிக்கண்டத்தின் புறப்பரப்பளவு:
இதில், a1, a2 ஆகிய இரண்டும் அடிக்கண்டத்தின் இரு அடிப்பல்கோணிகளின் பக்க அளவுகள்.
குறிப்புகள்[தொகு]
- ↑ The term "frustum" comes from Latin frustum meaning "piece" or "morsel". The English word is often misspelled as frustrum, a different Latin word cognate to the English word "frustrate".[1] The confusion between these two words is very old: a warning about them can be found in the Appendix Probi, and the works of Plautus include a pun on them.[2]
மேற்கோள்கள்[தொகு]
- ↑ Clark, John Spencer (1895), Teachers' Manual: Books I-VIII.. For Prang's complete course in form-study and drawing, Books 7–8, Prang Educational Company, p. 49.
- ↑ Fontaine, Michael (2010), Funny Words in Plautine Comedy, Oxford University Press, pp. 117, 154, ISBN 9780195341447.
- ↑ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, p. 67
- ↑ Nahin, Paul. An Imaginary Tale: The story of √−1. Princeton University Press. 1998
- ↑ "Mathwords.com: Frustum". பார்க்கப்பட்ட நாள் 17 July 2011.
- ↑ Al-Sammarraie, Ahmed T.; Vafai, Kambiz (2017). "Heat transfer augmentation through convergence angles in a pipe". Numerical Heat Transfer, Part A: Applications 72 (3): 197−214. doi:10.1080/10407782.2017.1372670.
வெளியிணைப்புகள்[தொகு]
- Derivation of formula for the volume of frustums of pyramid and cone பரணிடப்பட்டது 2009-03-04 at the வந்தவழி இயந்திரம் (Mathalino.com)
- Weisstein, Eric W., "Pyramidal frustum", MathWorld.
- Weisstein, Eric W., "Conical frustum", MathWorld.
- Paper models of frustums (truncated pyramids)
- Paper model of frustum (truncated cone)
- Design paper models of conical frustum (truncated cones)












![{\displaystyle A={\frac {n}{4}}\left[\left(a_{1}^{2}+a_{2}^{2}\right)\cot {\frac {\pi }{n}}+{\sqrt {\left(a_{1}^{2}-a_{2}^{2}\right)^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}\left(a_{1}+a_{2}\right)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57c9ba44195955a9024eca9605b00b44cdbe785a)
