நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றம்

n பொருட்களின் வரிசைமாற்றம் மற்றும் நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றம் ஆகியவற்றின் எண்ணிக்கை. n பொருட்களின் வரிசைமாற்றங்களின் எண்ணிக்கை = n! (n factorial). n பொருட்களின் நிலைத்த புள்ளிகளற்ற வரிசைமாற்றங்களின் (இந்த வரிசைமாற்றத்தில் அனைத்து n பொருட்களும் அதனதன் மூல இடத்தைவிட்டு மாறியிருக்கும்) எண்ணிக்கை =  !n (n உட்தொடர்பெருக்கம்)

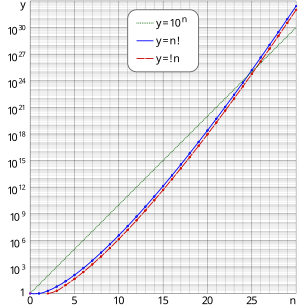
மதிப்புகளின் அட்டவணை
$n$	வரிசைமாற்றங்கள், $n!$	நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றங்கள், $!n$	${\frac {!n}{n!}}$
0	1 =1×100	1 =1×100	= 1
1	1 =1×100	0	= 0
2	2 =2×100	1 =1×100	= 0.5
3	6 =6×100	2 =2×100	≈0.33333 33333
4	24 =2.4×101	9 =9×100	= 0.375
5	120 =1.20×102	44 =4.4×101	≈0.36666 66667
6	720 =7.20×102	265 =2.65×102	≈0.36805 55556
7	5 040 ≈5.04×103	1 854 ≈1.85×103	≈0.36785 71429
8	40 320 ≈4.03×104	14 833 ≈1.48×104	≈0.36788 19444
9	362 880 ≈3.63×105	133 496 ≈1.33×105	≈0.36787 91887
10	3 628 800 ≈3.63×106	1 334 961 ≈1.33×106	≈0.36787 94643
11	39 916 800 ≈3.99×107	14 684 570 ≈1.47×107	≈0.36787 94392
12	479 001 600 ≈4.79×108	176 214 841 ≈1.76×108	≈0.36787 94413
13	6 227 020 800 ≈6.23×109	2 290 792 932 ≈2.29×109	≈0.36787 94412
14	87 178 291 200 ≈8.72×1010	32 071 101 049 ≈3.21×1010	≈0.36787 94412
15	1 307 674 368 000 ≈1.31×1012	481 066 515 734 ≈4.81×1011	≈0.36787 94412
16	20 922 789 888 000 ≈2.09×1013	7 697 064 251 745 ≈7.70×1012	≈0.36787 94412
17	355 687 428 096 000 ≈3.56×1014	130 850 092 279 664 ≈1.31×1014	≈0.36787 94412
18	6 402 373 705 728 000 ≈6.40×1015	2 355 301 661 033 953 ≈2.36×1015	≈0.36787 94412
19	121 645 100 408 832 000 ≈1.22×1017	44 750 731 559 645 106 ≈4.48×1016	≈0.36787 94412
20	2 432 902 008 176 640 000 ≈2.43×1018	895 014 631 192 902 121 ≈8.95×1017	≈0.36787 94412
21	51 090 942 171 709 440 000 ≈5.11×1019	18 795 307 255 050 944 540 ≈1.88×1019	≈0.36787 94412
22	1 124 000 727 777 607 680 000 ≈1.12×1021	413 496 759 611 120 779 881 ≈4.13×1020	≈0.36787 94412
23	25 852 016 738 884 976 640 000 ≈2.59×1022	9 510 425 471 055 777 937 262 ≈9.51×1021	≈0.36787 94412
24	620 448 401 733 239 439 360 000 ≈6.20×1023	228 250 211 305 338 670 494 289 ≈2.28×1023	≈0.36787 94412
25	15 511 210 043 330 985 984 000 000 ≈1.55×1025	5 706 255 282 633 466 762 357 224 ≈5.71×1024	≈0.36787 94412
26	403 291 461 126 605 635 584 000 000 ≈4.03×1026	148 362 637 348 470 135 821 287 825 ≈1.48×1026	≈0.36787 94412
27	10 888 869 450 418 352 160 768 000 000 ≈1.09×1028	4 005 791 208 408 693 667 174 771 274 ≈4.01×1027	≈0.36787 94412
28	304 888 344 611 713 860 501 504 000 000 ≈3.05×1029	112 162 153 835 443 422 680 893 595 673 ≈1.12×1029	≈0.36787 94412
29	8 841 761 993 739 701 954 543 616 000 000 ≈8.84×1030	3 252 702 461 227 859 257 745 914 274 516 ≈3.25×1030	≈0.36787 94412
30	265 252 859 812 191 058 636 308 480 000 000 ≈2.65×1032	97 581 073 836 835 777 732 377 428 235 481 ≈9.76×1031	≈0.36787 94412

சேர்வியல் கணிதத்தில் நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றம் (derangement) என்பது ஒரு கணத்திலுள்ள உறுப்புகளின் குறிப்பிடவகையானதொரு வரிசை மாற்றமாகும். இந்த வரிசைமாற்றத்தில் வரிசைமாற்றத்துள்ளாகும் கணத்தின் உறுப்புகள் அனைத்தும் அதனதன் மூல இடத்தில் இருக்காது. அதாவது இந்த வரிசைமாற்றத்தில் நிலைத்த புள்ளிகளே இருக்காது.

n உறுப்புகளுடைய கணத்தின் நிலைத்த புள்ளிகளற்ற வரிசைமாற்றத்தின் எண்ணிக்கை "உட்தொடர்பெருக்கம்" ("subfactorial") அல்லது "n ஆவது நிலைத்தபுள்ளிகளற்ற வரிசை மாற்றத்தின் எண்" என அழைக்கப்படுகிறது.

இந்த எண்ணிக்கையின் குறியீடுகள்:  !n, D_n, d_n, or n¡.

!n இன் மதிப்பு n!/e இன் மதிப்பிற்கு மிக அண்மையிலான முழுஎண் மதிப்பாகும். இதில் n! என்பது n இன் தொடர்பெருக்கம் மற்றும் e ஆனது ஆய்லர் மாறிலி.

நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றங்களின் எண்ணிக்கையை அறியும் முயற்சியில் 1708 இல் முதன்முறையாக ஈடுபட்டவர் கணிதவியலாளர் பியரே ரேமான்டு டி மான்ட்மார்ட் ஆவார். 1713 இல் இவர் அந்த முயற்சியில் வெற்றிபெற்ற அதேசமயத்தில் கணிதவியலாளர் நிக்கோலசு பெர்னொலியும் அதனைக் கண்டறிந்தார்.

எடுத்துக்காட்டு

24 வரிசைமாற்றங்களில் 9 நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றங்கள் சிவப்புக்கட்டமிட்டுக் காட்டப்பட்டுள்ளது

A, B, C, D என்ற நான்கு மாணவர்களுக்குத் தேர்வு நடத்திய ஆசிரியர் ஒருவர், ஒரு மாணவன் தனது விடைத்தாளைத் தானே மதிப்பிடக்கூடாதென்ற நிபந்தனையோடு தேர்வு விடைத்தாட்களை அவர்களைக் கொண்டு மதிப்பிட விரும்புகிறார். இதனை எத்தனை வேறுபட்ட வழிகளில் அவர் செய்திருக்கக்கூடும் என்பது 4 பொருட்களின் நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றங்களின் எண்ணிக்கைக்குச் சமமாகும்.

A, B, C, D என்ற நான்கு மாணவர்களை வரிசைமாற்றக் கிடைக்கும் வழிகளின் எண்ணிக்கை 24 ஆகும். அவை கீழே தரப்பட்டுள்ளன. அவற்றுள் 9 மட்டுமே நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றங்கள் 9 (நீலநிறசாய்வெழுத்துகளில்) மட்டுமே உள்ளதையும், மீதமுள்ள அமைப்புகளில் (சிவப்புநிற தடித்த எழுத்துகளில்) A, B, C, D ஆகிய நான்கு எழுத்துக்களும் அதனதன் இடத்திலேயே மாறாமல் இருப்பதையும் காணலாம்:

ABCD,	ABDC,	ACBD,	ACDB,	ADBC,	ADCB,
BACD,	BADC,	BCAD,	BCDA,	BDAC,	BDCA,
CABD,	CADB,	CBAD,	CBDA,	CDAB,	CDBA,
DABC,	DACB,	DBAC,	DBCA,	DCAB,	DCBA.

நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றங்களின் எண்ணிக்கை காணல்

• n பொருட்களின் நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றத்தை பின் வரும் எடுத்துக்காட்டாகக் கொள்ளலாம்:

1, 2, ..., n என்ற எண்களிடப்பட்ட n நபர்களும் n தொப்பிகளும் உள்ளன என்க.

இதில் ஒருவர் ஒரு சமயத்தில் ஒரு தொப்பியை மட்டும் எடுக்கலாம் என்றால் அச்செயல் எத்தனை வேறுபட்ட வழிகளில் செய்யப்படலாம் என்பது n வரிசைமாற்றங்களின் எண்ணிக்கை n!

மாறாக ஒரு நபர் தனக்களிக்கப்பட்டுள்ள எண்ணுள்ள தொப்பியைத் தவிர பிற தொப்பிகளில் ஒன்றை மட்டுமே எடுக்கலாம் என்றால் அது நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றங்களின் எண்ணிக்கை !n

எண் "1" என்ற நபர் ஒரு தொப்பியை எடுக்கிறார் என்றால் அதனை அவர் n − 1 வழிகளில் செய்யலாம். ஏனெனில் அவர் "1" எண்ணிடப்பட்ட தொப்பியை எடுக்கக்கூடாது. அவர் எடுத்த தொப்பியின் எண் i என்க.

இப்பொழுது இரு சாத்தியக்கூறுகள் எழுகின்றன:

1. i எண்ணிடப்பட்ட நபர் "1" எண்ணிடப்பட்ட தொப்பியை எடுக்கவில்லை.

இந்நிலையில் இது n − 1 நபர்கள் மற்றும் n − 1 தொப்பிகள் அடங்கிய நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றமாக அமைகிறது. (ஒவ்வொரு நபருக்கும் ஒரு வாய்ப்பு தடுக்கப்படுகிறது (எடுத்துக்காட்டாக i' நபருக்கு தொப்பி எண் 1 தடுக்கப்பட்டுள்ளது).

2. i நபர் தொப்பி எண் "1" ஐ எடுக்கிறார்.

இந்நிலையில் இது n − 2 நபர்கள் மற்றும் n − 2 தொப்பிகளின் நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றக் கணக்காக அமைகிறது..

இவ்விரு சாத்தியக்கூறுகளில் ஏதேனுமொன்று நிகழும் என்பதால் n நபர்கள் மற்றும் n தொப்பிகளின் நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றங்களின் எண்ணிக்கையின் மதிப்பு:

$!n=(n-1)(!(n-1)+!(n-2)).\,$

இதில் துவக்க மதிப்புகள்: !0 = 1 மற்றும் !1 = 0 எனக் கொள்ளப்படுகிறது.

• n பொருட்களின் நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றத்திற்கு பின்வரும் வாய்ப்பாடுகளுமுள்ளன:

$!n=n!\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}},$

$!n=\left[{\frac {n!}{e}}\right]=\left\lfloor {\frac {n!}{e}}+{\frac {1}{2}}\right\rfloor ,\quad n\geq 1$

இதில் $\left[x\right]$ அண்மை முழுஎண் சார்பு, $\left\lfloor x\right\rfloor$ தரைச் சார்பு.

$!n=\left\lfloor (e+e^{-1})n!\right\rfloor -\lfloor en!\rfloor ,\quad n\geq 2,$

$!n=n!-\sum _{i=1}^{n}{n \choose i}\cdot !(n-i),$

• n பொருட்களின் நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றத்திற்கு மீளும் வாய்ப்பாடு:

$!n=n\left(!(n-1)\right)+(-1)^{n}$

• n = 0, எனத் துவக்கம் கொள்ள, n பொருட்களின் நிலைத்தபுள்ளிகளற்ற வரிசைமாற்றங்களி எண்ணிக்ககை::

1, 0, 1, 2, 9, 44, 265, 1854, 14833, 133496, 1334961, 14684570, 176214841, 2290792932, ... (OEIS-இல் வரிசை A000166)

.

வெளியிணைப்புகள்

• Baez, John (2003). "Let's get deranged!" (PDF).
• Bogart, Kenneth P.; Doyle, Peter G. (1985). "Non-sexist solution of the ménage problem".
• Dickau, Robert M. "Derangement diagrams". Mathematical Figures Using Mathematica.
• Hassani, Mehdi. "Derangements and Applications". Journal of Integer Sequences (JIS), Volume 6, Issue 1, Article 03.1.2, 2003.
• Weisstein, Eric W. "Derangement". MathWorld–A Wolfram Web Resource.