பயனர்:Booradleyp/test: திருத்தங்களுக்கு இடையிலான வேறுபாடு
இப்பக்கத்தில் இருந்த உள்ளடக்கங்கள் நீக்கப்பட்டுவிட்டன |
No edit summary |
||
| வரிசை 1: | வரிசை 1: | ||
யூக்ளிடின் வடிவவியலில் பிரம்ம குப்தரின் வாய்ப்பாடு என்பது (Brahmagupta's formula) நாற்கரத்தின் பரப்பு காணும் ஒரு வாய்ப்பாடு. ஒரு நாற்கரத்தின் பக்கங்களின் நீளங்களும் சில கோணங்களும் தரப்பட்டிருக்கும் போது இவ்வாய்ப்பாட்டைப் பயன்படுத்தி அந்நாற்கரத்தின் பரப்பைக் காணாலாம். இவ்வாய்ப்பாட்டின் பொது படிவம் ஒரு வட்டத்துக்குள் வரையப்பட்ட நாற்கரத்தின் பரப்பைத் தரும். |
|||
== அடிப்படை படிவம் == |
|||
பிரம்ம குப்தரின் வாய்ப்பாட்டின் எளிமையானதும் எளிதில் மனதில் பதியக்கூடியதுமான படிவம், ''a'', ''b'', ''c'', ''d'' -ஐ பக்க நீளங்களாகக் கொண்ட வட்ட நாற்கரத்தின் பரப்பைத் தருகிறது: |
|||
: <math>K=\sqrt{(s-a)(s-b)(s-c)(s-d)}</math> |
|||
இங்கு ''s'', நாற்கரத்தின் அரைச்சுற்றளவு. |
|||
: <math>s=\frac{a+b+c+d}{2}\cdot</math> |
|||
:<math>s-a= \frac{-a+b+c+d}{2}</math> |
|||
:<math>s-b= \frac{a-b+c+d}{2}</math> |
|||
:<math>s-c= \frac{a+b-c+d}{2}</math> |
|||
:<math>s-d= \frac{a+b+c-d}{2}</math> |
|||
இவ்வாய்ப்பாடு முக்கோணத்தின் பரப்பு காணும் ஹீரோனின் வாய்ப்பாட்டின் பொதுமைப்படுத்தப்பட்ட படிவமாக அமைகிறது. பிரம்ம குப்தரின் வாய்ப்பாட்டில் '''d''' -ன் மதிப்பு பூச்சியத்தை நெருங்குவதாகக் கொண்டால் ஹீரோனின் வாய்ப்பாடு கிடைக்கும். அதாவது ஒரு பக்கத்தின் நீளம் பூச்சியமாக உள்ள நாற்கரமாக முக்கோணத்தைக் கொள்ளலாம். |
|||
இவ்வாய்ப்பாட்டின் மற்றொரு படிவம்: |
|||
: <math>K=\frac{\sqrt{(a^2+b^2+c^2+d^2)^2+8abcd-2(a^4+b^4+c^4+d^4)}}{4}\cdot</math> |
|||
== நிறுவல் == |
|||
[[Image:Brahmaguptas formula.svg|frame|right|Diagram for reference]] |
|||
வட்ட நாற்கரம் ABCD -ன் பரப்பு = <math>\triangle ADB</math> -ன் பரப்பு+ <math>\triangle BDC</math> -ன் பரப்பு |
|||
:<math>= \frac{1}{2}pq\sin A + \frac{1}{2}rs\sin C.</math> |
|||
<math>ABCD</math>, ஒரு வட்ட நாற்கரம் என்பதால்: |
|||
:<math>\angle DAB = 180^\circ - \angle DCB.</math> |
|||
:<math>\sin A = \sin C.</math> |
|||
: ஃ <math>\mbox{Area} = \frac{1}{2}pq\sin A + \frac{1}{2}rs\sin A</math> |
|||
:<math>(\mbox{Area})^2 = \frac{1}{4}\sin^2 A (pq + rs)^2</math> |
|||
:<math>4(\mbox{Area})^2 = (1 - \cos^2 A)(pq + rs)^2 = (pq + rs)^2 - \cos^2 A (pq + rs)^2.\,</math> |
|||
<math>\triangle</math>''ADB'' மற்றும் <math>\triangle </math>''BDC'', இரண்டின் பொதுப்பக்கம் DB-ன் மதிப்பைக் கொசைன் வாய்ப்பாட்டின் மூலம் காண: |
|||
:<math>DB = p^2 + q^2 - 2pq\cos A = r^2 + s^2 - 2rs\cos C. \,</math> |
|||
<math>\cos C = \cos(\pi – A) = -\cos A</math> ( <math>A</math>, <math>C</math> மிகைநிரப்புக் கோணங்கள்) |
|||
இதைப்பயன்படுத்த: |
|||
:<math> p^2 + q^2 - 2pq\cos A = r^2 + s^2 +2rs\cos A. \,</math> |
|||
:<math>2\cos A (pq + rs) = p^2 + q^2 - r^2 - s^2. \,</math> |
|||
:<math>\cos A (pq + rs) = \frac{p^2 + q^2 - r^2 - s^2}{2}. \,</math> |
|||
வர்க்கப்படுத்த: |
|||
:<math>\cos ^2A (pq + rs)^2 = \frac{(p^2 + q^2 - r^2 - s^2)^2}{4}. \,</math> |
|||
இதனைப் பரப்பு வாய்ப்பாட்டில் பிரதியிட: |
|||
:<math>4(\mbox{Area})^2 = (pq + rs)^2 - \frac{1}{4}(p^2 + q^2 - r^2 - s^2)^2</math> |
|||
:<math>16(\mbox{Area})^2 = 4(pq + rs)^2 - (p^2 + q^2 - r^2 - s^2)^2, \,</math> |
|||
:<math>(2(pq + rs) - p^2 - q^2 + r^2 +s^2)(2(pq + rs) + p^2 + q^2 -r^2 - s^2) \,</math> |
|||
:<math>= ( (r+s)^2 - (p-q)^2 )( (p+q)^2 - (r-s)^2 ) \,</math> |
|||
:<math>= (q+r+s-p)(p+r+s-q)(p+q+s-r)(p+q+r-s). \,</math> |
|||
<math>S = \frac{p+q+r+s}{2},</math> எனக் கொண்டால் |
|||
:<math>16(\mbox{Area})^2 = 16(S-p)(S-q)(S-r)(S-s). \,</math> |
|||
வர்க்கமூலம் காண: |
|||
:<math>\mbox{Area} = \sqrt{(S-p)(S-q)(S-r)(S-s)}.</math> |
|||
== வட்டத்துக்குள் அமையாத நாற்கரங்களுக்கு நீட்டிப்பு == |
|||
வட்டத்துக்குள் அமையாத நாற்கரங்களின் பரப்பு காண்பதற்கு பிரம்ம குப்தரின் வாய்ப்பாட்டை நீட்டிக்கலாம். இதற்கு நாற்கரங்களின் எதிர்க் கோணங்களின் அளவுகளைக் கருத்தில் கொள்ளல் வேண்டும். |
|||
: <math>K=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\theta}</math> |
|||
இங்கு θ நாற்கரத்தின் ஏதேனும் ஒரு சோடி எதிர்க் கோணங்களின் கூட்டுத்தொகையில் பாதி. இரண்டு சோடி எதிர்க் கோணங்களில் எந்த சோடியை வேண்டுமானாலும் எடுத்துக் கொள்ளலாம். ஏனெனில் மற்றொரு சோடி எதிர்க்கோணங்களின் கூட்டுத்தொகையில் பாதி 180- θ -ஆக இருக்கும். cos(180° − θ) = −cosθ, cos<sup>2</sup>(180° − θ) = cos<sup>2</sup>θ.) |
|||
தரப்பட்ட பக்க நீளங்களைக் கொண்ட நாற்கரங்களிலேயே வட்ட நாற்கரங்கள் தான் மீப்பெரு பரப்புடையவை. மேலேயுள்ள பரப்பு வாய்ப்பாடு பிரெட்ஷ்னீடரின் வாய்ப்பாடாகும். |
|||
பொது நாற்கரங்களின் பரப்பு வாய்ப்பாட்டிலிருந்து வட்ட நாற்கரங்களின் பரப்பு காணும் வாய்ப்பாட்டைப் பெறுதல்: |
|||
வட்ட நாற்கரங்களின் பண்பின்படி அதன் எதிர்க் கோணங்கள் மிகைநிரப்புக் கோணங்கள். எனவே அவற்றின் கூடுதல் 180°, θ = 90°. |
|||
: ஃ<math>abcd\cos^2\theta=abcd\cos^2 \left(90^\circ\right)=abcd\cdot0=0, \,</math> |
|||
எனவே பரப்பு வாய்ப்பாட்டில் இதைப் பிரதியிட: |
|||
:<math>K=\sqrt{(s-a)(s-b)(s-c)(s-d)}</math> - இது பிரம்ம குப்தரின் வாய்ப்பாடு. |
|||
பிரம்ம குப்தரின் வாய்ப்பாடு கிடைக்கும். |
|||
ஜூலியன் கூலிட்ஜ் -ஆல் நிறுவப்பட்ட பொது குவிவு நாற்கரங்களின் பரப்பு காணும் வாய்ப்பாடு:<ref>J. L. Coolidge, "A Historically Interesting Formula for the Area of a Quadrilateral", ''American Mathematical Monthly'', '''46''' (1939) pp. 345-347.</ref> |
|||
: <math>K=\sqrt{(s-a)(s-b)(s-c)(s-d)-\textstyle{1\over4}(ac+bd+pq)(ac+bd-pq)}\,</math> |
|||
இங்கு ''p'' மற்றும் ''q'' -நாற்கரத்தின் மூலைவிட்டங்களின் நீளங்கள். டாலமியின் தேற்றப்படி, ஒரு வட்ட நாற்கரத்திற்கு, <math>pq=ac+bd</math> -ஆக இருக்கும். இம்மதிப்பைப் பிரதியிட கூலிட்ஜின் வாய்ப்பாடு, பிரம்ம குப்தரின் வாய்ப்பாடாக மாறும். |
|||
== தொட்ர்புள்ள பிற தேற்றங்கள் == |
|||
முக்கோணங்களின் பரப்பு காணும் ஹீரோனின் வாய்ப்பாடு - நாற்கரத்தின் பக்க நீளம் ''d'' = 0 எனக் கொள்வதால் கிடைக்கும் சிறப்பு வகை. |
|||
பிரம்ம குப்தரின் பொது வாய்ப்பாட்டிற்கும் நீட்டிக்கப்பட்ட வாய்ப்பாட்டிற்கும் உள்ள தொடர்பு, கொசைன் விதியானது பித்தகோரஸ் தேற்றத்திற்கு நீட்டிக்கப்படுதலுக்குச் சமமானது. |
|||
==வெளி இணைப்புகள்== |
|||
* [http://mathworld.wolfram.com/BrahmaguptasFormula.html MathWorld: Brahmagupta's formula] |
|||
== மேற்கோள்கள் == |
|||
{{reflist}} |
|||
{{planetmath|id=3594|title=proof of Brahmagupta's formula}} |
|||
[[ar:معادلة براهماغوبتا]] |
|||
[[ca:Fórmula de Brahmagupta]] |
|||
[[de:Formel von Brahmagupta]] |
|||
[[en: Brahmagupta's formula]] |
|||
[[es:Fórmula de Brahmagupta]] |
|||
[[fr:Formule de Brahmagupta]] |
|||
[[ko:브라마굽타의 공식]] |
|||
[[it:Formula di Brahmagupta]] |
|||
[[nl:Formule van Brahmagupta]] |
|||
[[ja:ブラーマグプタの公式]] |
|||
[[km:រូបមន្តប្រាម៉ាហ្គឹបតា]] |
|||
[[ru:Формула Брахмагупты]] |
|||
[[sr:Формула Брамагупте]] |
|||
[[fi:Brahmaguptan kaava]] |
|||
[[zh:婆羅摩笈多公式]] |
|||
04:09, 7 பெப்பிரவரி 2012 இல் நிலவும் திருத்தம்
யூக்ளிடின் வடிவவியலில் பிரம்ம குப்தரின் வாய்ப்பாடு என்பது (Brahmagupta's formula) நாற்கரத்தின் பரப்பு காணும் ஒரு வாய்ப்பாடு. ஒரு நாற்கரத்தின் பக்கங்களின் நீளங்களும் சில கோணங்களும் தரப்பட்டிருக்கும் போது இவ்வாய்ப்பாட்டைப் பயன்படுத்தி அந்நாற்கரத்தின் பரப்பைக் காணாலாம். இவ்வாய்ப்பாட்டின் பொது படிவம் ஒரு வட்டத்துக்குள் வரையப்பட்ட நாற்கரத்தின் பரப்பைத் தரும்.
அடிப்படை படிவம்
பிரம்ம குப்தரின் வாய்ப்பாட்டின் எளிமையானதும் எளிதில் மனதில் பதியக்கூடியதுமான படிவம், a, b, c, d -ஐ பக்க நீளங்களாகக் கொண்ட வட்ட நாற்கரத்தின் பரப்பைத் தருகிறது:
இங்கு s, நாற்கரத்தின் அரைச்சுற்றளவு.
இவ்வாய்ப்பாடு முக்கோணத்தின் பரப்பு காணும் ஹீரோனின் வாய்ப்பாட்டின் பொதுமைப்படுத்தப்பட்ட படிவமாக அமைகிறது. பிரம்ம குப்தரின் வாய்ப்பாட்டில் d -ன் மதிப்பு பூச்சியத்தை நெருங்குவதாகக் கொண்டால் ஹீரோனின் வாய்ப்பாடு கிடைக்கும். அதாவது ஒரு பக்கத்தின் நீளம் பூச்சியமாக உள்ள நாற்கரமாக முக்கோணத்தைக் கொள்ளலாம்.
இவ்வாய்ப்பாட்டின் மற்றொரு படிவம்:
நிறுவல்
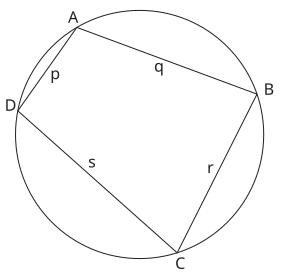
வட்ட நாற்கரம் ABCD -ன் பரப்பு = -ன் பரப்பு+ -ன் பரப்பு
, ஒரு வட்ட நாற்கரம் என்பதால்:
- ஃ
ADB மற்றும் BDC, இரண்டின் பொதுப்பக்கம் DB-ன் மதிப்பைக் கொசைன் வாய்ப்பாட்டின் மூலம் காண:
பாகுபடுத்தல் தோல்வி (தொடரமைப்புத் தவறு): {\displaystyle \cos C = \cos(\pi – A) = -\cos A} ( , மிகைநிரப்புக் கோணங்கள்)
இதைப்பயன்படுத்த:
வர்க்கப்படுத்த:
இதனைப் பரப்பு வாய்ப்பாட்டில் பிரதியிட:
எனக் கொண்டால்
வர்க்கமூலம் காண:
வட்டத்துக்குள் அமையாத நாற்கரங்களுக்கு நீட்டிப்பு
வட்டத்துக்குள் அமையாத நாற்கரங்களின் பரப்பு காண்பதற்கு பிரம்ம குப்தரின் வாய்ப்பாட்டை நீட்டிக்கலாம். இதற்கு நாற்கரங்களின் எதிர்க் கோணங்களின் அளவுகளைக் கருத்தில் கொள்ளல் வேண்டும்.
இங்கு θ நாற்கரத்தின் ஏதேனும் ஒரு சோடி எதிர்க் கோணங்களின் கூட்டுத்தொகையில் பாதி. இரண்டு சோடி எதிர்க் கோணங்களில் எந்த சோடியை வேண்டுமானாலும் எடுத்துக் கொள்ளலாம். ஏனெனில் மற்றொரு சோடி எதிர்க்கோணங்களின் கூட்டுத்தொகையில் பாதி 180- θ -ஆக இருக்கும். cos(180° − θ) = −cosθ, cos2(180° − θ) = cos2θ.)
தரப்பட்ட பக்க நீளங்களைக் கொண்ட நாற்கரங்களிலேயே வட்ட நாற்கரங்கள் தான் மீப்பெரு பரப்புடையவை. மேலேயுள்ள பரப்பு வாய்ப்பாடு பிரெட்ஷ்னீடரின் வாய்ப்பாடாகும்.
பொது நாற்கரங்களின் பரப்பு வாய்ப்பாட்டிலிருந்து வட்ட நாற்கரங்களின் பரப்பு காணும் வாய்ப்பாட்டைப் பெறுதல்:
வட்ட நாற்கரங்களின் பண்பின்படி அதன் எதிர்க் கோணங்கள் மிகைநிரப்புக் கோணங்கள். எனவே அவற்றின் கூடுதல் 180°, θ = 90°.
- ஃ
எனவே பரப்பு வாய்ப்பாட்டில் இதைப் பிரதியிட:
- - இது பிரம்ம குப்தரின் வாய்ப்பாடு.
பிரம்ம குப்தரின் வாய்ப்பாடு கிடைக்கும்.
ஜூலியன் கூலிட்ஜ் -ஆல் நிறுவப்பட்ட பொது குவிவு நாற்கரங்களின் பரப்பு காணும் வாய்ப்பாடு:[1]
இங்கு p மற்றும் q -நாற்கரத்தின் மூலைவிட்டங்களின் நீளங்கள். டாலமியின் தேற்றப்படி, ஒரு வட்ட நாற்கரத்திற்கு, -ஆக இருக்கும். இம்மதிப்பைப் பிரதியிட கூலிட்ஜின் வாய்ப்பாடு, பிரம்ம குப்தரின் வாய்ப்பாடாக மாறும்.
தொட்ர்புள்ள பிற தேற்றங்கள்
முக்கோணங்களின் பரப்பு காணும் ஹீரோனின் வாய்ப்பாடு - நாற்கரத்தின் பக்க நீளம் d = 0 எனக் கொள்வதால் கிடைக்கும் சிறப்பு வகை.
பிரம்ம குப்தரின் பொது வாய்ப்பாட்டிற்கும் நீட்டிக்கப்பட்ட வாய்ப்பாட்டிற்கும் உள்ள தொடர்பு, கொசைன் விதியானது பித்தகோரஸ் தேற்றத்திற்கு நீட்டிக்கப்படுதலுக்குச் சமமானது.
வெளி இணைப்புகள்
மேற்கோள்கள்
- ↑ J. L. Coolidge, "A Historically Interesting Formula for the Area of a Quadrilateral", American Mathematical Monthly, 46 (1939) pp. 345-347.
This article incorporates material from ப்ளேனட் மேத் தளத்தில் proof of Brahmagupta's formula, which is licensed under the Creative Commons Attribution/Share-Alike License.




































