வளைவு மையம்
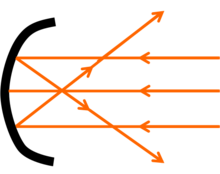

வடிவவியலில், ஒரு வளைகோட்டின் வளைவு மையம் (center of curvature) என்பது அவ்வளைகோட்டின் வளைவு ஆரத்திற்குச் சமமான தூரத்தில் செங்கோட்டின் மீதமையும் புள்ளியைக் குறிக்கும். வளைவின் மதிப்பு, பூச்சியமெனில் வளைவு மையமானது முடிவிலிப் புள்ளியாக இருக்கும். ஒரு வளைகோட்டின் வளைவு மையம் அதன் கொஞ்சு வட்டத்தின் மையமாக இருக்கும். வளைவு மையம் வளைகோட்டின் இரு நுண்ணளவு நெருக்கமான இரு செங்கோடுகள் சந்திக்கும் புள்ளியே அவ்வளைகோட்டின் வளைவு மையமென கணிதவியலாளர் அகுஸ்டின்-லூயி கோசி வரையறுத்துள்ளார்.[1] வளைகோட்டின் மீதுள்ள ஒவ்வொரு புள்ளிக்கும் வளைவு மையங்களின் இயங்குவரையானது அவ்வளைகோட்டின் அலர் வளைவரையாகும் (மலரி). ஒளியியலில் வில்லைகள், ஆடிகள் ஆகியவற்றின் ஆய்வுகளில் வளைவு மையம் பயன்படுகிறது (காண்க:வளைவு ஆரம்).
ஒரு வில்லை அல்லது ஆடியில் விழும் ஒளிக்கதிர்கள் ஒருங்குவது போன்று (குவி வில்லைகள், குழி ஆடிகள்) அல்லது விரிவது போன்று (குழி வில்லைகள், குவி ஆடிகள்) தோன்றும் புள்ளிக்கும் அவ்வில்லை அல்லது ஆடிக்கும் இடைப்பட்டக் கோள தொலைவாகவும் வரையறுக்கலாம்.[2]
மேலும் காண்க[தொகு]
மேற்கோள்கள்[தொகு]
- ↑ *Borovik, Alexandre; Katz, Mikhail G. (2011), "Who gave you the Cauchy--Weierstrass tale? The dual history of rigorous calculus", Foundations of Science, 17 (3): 245–276, arXiv:1108.2885, doi:10.1007/s10699-011-9235-x, S2CID 119320059
- ↑ Trinklein, Frederick E. (1992). Modern physics (7th ). Austin: Holt, Rinehart and Winston. பன்னாட்டுத் தரப்புத்தக எண்:0-03-074317-6. இணையக் கணினி நூலக மையம்:25702491.
நூலடைவு[தொகு]
- *Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-0087-9
