பொன் விகிதம்

கணிதவியலிலும் கலையிலும் எவையேனும் இரு அளவுகளின் கூடுதலுக்கும் அவற்றில் பெரிய அளவுக்குமான விகிதமானது, பெரிய அளவுக்கும் சிறிய அளவுக்குமான விகிதத்திற்குச் சமமாக இருந்தால் அந்த இரு அளவுகளும் பொன் விகிதத்தில் (golden ratio) அமைந்துள்ளன எனப்படுகின்றன. இவ்விகிதத்தின் மதிப்பு ஒரு விகிதமுறா மாறிலி எண்ணாகும். இதன் தோராயமான மதிப்பு 1.61803398874989.[1] பொன் விகிதத்தின் குறியீடு கிரேக்க மொழியின் சிறிய எழுத்து () (phi).
- (இவ்வெழுத்தின் தலைகீழி அல்லது = (Phi).இது கிரேக்க மொழியின் பெரிய எழுத்து.)
விகிதமுறா எண்களின் கணத்தில் இச்சமன்பாட்டிற்கு ஒரு நேர்மத் தீர்வு உள்ளது:
- .
[1] பொன் விகிதமானது கவின்கலை, ஓவியம், கட்டிடக்கலை, புத்தக வடிவமைப்பு, இயற்கை, இசை, நிதிச்சந்தை...என பல்வகையான துறைகளிலும் பரந்து காணப்படுகிறது.
20 ம் நூற்றாண்டிலிருந்து, பல ஓவியர்களும், கட்டிடக் கலைஞர்களும் தமது படைப்புகளில் பொன் விகிதத்தைப் பயன்படுத்தினார்கள். இவர்களின் பயன்பாடு பொதுவாக பொன் செவ்வக வடிவில் அமைந்தது. நீளமும் அகலமும் பொன் விகிதத்தில் அமைந்த இச்செவ்வகம் அழகியல் அடிப்படையில் மனதுக்கு உகந்தது என நம்பப்பட்டது. இவ்விகிதத்தின் தனித்துவமான இயல்புகள் கணிதவியலாளர்களை ஆராயத் தூண்டியது.
வரலாறு[தொகு]


பொன் விகிதம், பல்வேறு வகையான ஆர்வங்களைக் கொண்ட அறிஞர்களை 2,400 ஆண்டுகளாக ஈர்த்து வந்துள்ளது.
எக்காலத்தும் சிறந்த சில கணித மூளைகளான பண்டைக் கிரேக்கத்தின் பித்தாகரஸ், இயூக்கிளிட் ஆகியோரில் இருந்து, மத்தியகால இத்தாலியக் கணிதவியலாளராகிய ஃபிபோனாசி, மறுமலர்ச்சிக்கால வானியலாளர் ஜொஹான்னஸ் கெப்லர், ஆகியோரூடாக இன்றைய அறிவியலாளர்களான ஆக்ஸ்போர்ட் இயற்பியலாளர் ரோஜர் பென்ரோஸ் வரை உள்ள அறிஞர்கள் இந்த எளிமையான விகிதத்தின் இயல்புகள் பற்றி ஆராய்வதற்காகப் பெருமளவு நேரத்தைச் செலவு செய்துள்ளனர். ஆனால், இவ்விகிதத்தின் மீதான ஆர்வம் கணிதவியலாளர்களுக்கு மட்டும் ஏற்பட்டதல்ல. உயிரியலாளர்கள், கலைஞர்கள், இசைக்கலைஞர்கள், வரலாற்றாளர்கள், கட்டிடக்கலைஞர்கள், உளவியலாளர்கள் போன்றோரும் இதுபற்றிச் சிந்தித்து இதன் கவர்ச்சியின் அடிப்படைகள் பற்றி விவாதித்துள்ளனர். உண்மையில், கணிதவியலின் வரலாற்றில் வேறெந்த எண்ணையும் விட அதிகமாக எல்லாத் துறைகளையும் சேர்ந்த சிந்தனையாளர்களையும் பொன் விகிதம் ஈர்த்துள்ளது என்று சொன்னால் நியாயமாக இருக்கக்கூடும்.
—மரியோ லிவியோ, பொன் விகிதம்: "பை"யின் வரலாறு, The World's Most Astonishing Number
வடிவவியலில் அதிகமாக பொன் விகிதம் காணப்படுவதால் பண்டையக் கிரேக்கர்கள் இது பற்றி ஆய்வுகள் செய்துள்ளனர். ஒழுங்கு நட்சத்திர ஐங்கோணம் மற்றும் ஒழுங்கு ஐங்கோணம் பற்றிய வடிவவியலில் ஒரு கோட்டை முடிவு மற்றும் இடை விகிதத்தில் பிரிப்பது முக்கியமானதாக அமைகிறது. இக் கருத்துருவை பித்தாகரஸ் அல்லது அவரைப் பின்பற்றுவோர் கண்டுபிடித்திருக்க வேண்டுமென கிரேக்கர்கள் நம்புகின்றனர். ஒழுங்கான ஐங்கோணத்தை உள்ளடக்கிய ஒழுங்கான நட்சத்திர ஐங்கோண வடிவம் பித்தாகோரியர்களின் சின்னமாக உள்ளது.
கணக்கிடுதல்[தொகு]
a மற்றும் b -இரண்டும் பொன் விகிதத்தில் அமைந்திருந்தால்:
- .
- -ஐப் பின்வருமாறு சுருக்க:
- கிடைக்கிறது.
ஆனால் :
எனவே
φ -ஆல் பெருக்க:
- .
இருபடி வாய்ப்பாட்டைப் பயன்படுத்தப் பின்வரும் நேர்மத் தீர்வு கிடைக்கும்:
- .
கணிதத்தில்[தொகு]
பொன் விகிதத்தின் இணை[தொகு]
φ -ன் இருபடிச் சமன்பாட்டின் எதிர்த் தீர்வு (இணையியத் தீர்வு):
- .
இதன் எண் மதிப்பு (≈ 0.618) = b/a. சில சமயங்களில் இம்மதிப்பு பொன் விகிதத்தின் இணை என அழைக்கப்படுகிறது.[2] இதன் குறியீடு Φ:
- .
மாறாக Φ பின்வருமாறும் தரப்படலாம்:
- .
இதிலிருந்து நேர்ம எண்களுக்குள் பொன் விகிதத்தின் பின்வரும் தனித்த பண்பினை அறியலாம்:
- .
அல்லது இதன் தலைகீழி:
- .
அதாவது:
0.61803... : 1 = 1 : 1.61803....
மாற்று வடிவங்கள்[தொகு]
- φ = 1 + 1/φ -சமன்பாட்டை மீள்வரு முறையில் விரித்து பொன் விகிதத்தினை தொடரும் பின்னவடிவில் பெறலாம்:[3]
- φ2 = 1 + φ சமன்பாட்டிலிருந்து பொன் விகிதத்தை தொடர்ச்சியான வர்க்கமூல (முடிவுறா விகிதமுறா மூலம்) வடிவில் பெறலாம்:
- .
- பொன் விகிதத்தை முடிலாத் தொடராகப் பெறலாம்:[4]
- மேலும் பல வடிவங்கள்:
இவற்றிலிருந்து ஒழுங்கு ஐங்கோணத்தின் மூலைவிட்டத்தின் நீளமானது அதன் பக்கத்தின் நீளத்தைப்போல் φ மடங்கு என்பதையும் ஐந்துமுனையுடைய நட்சத்திர வடிவத்தில் இதுபோன்ற தொடர்புகளையும் அறியலாம்.
வடிவவியல்[தொகு]
ஒரு கோட்டுத்துண்டை பொன் விகிதத்தில் பிரித்தல்[தொகு]
ஒரு கோட்டுத்துண்டை பின்வரும் வடிவியல் வரைமுறையில் பொன் விகிதத்தில் பிரிக்கலாம்:

- தரப்பட்ட கோட்டுத்துண்டு AB -க்குச் செங்குத்தாகவும் அதன் நீளத்தில் பாதியாகவும் உள்ள கோட்டுத்துண்டு BC வரைய வேண்டும். செம்பக்கம் AC வரைய வேண்டும்.
- C -ஐ மையமாகவும் BC -ஐ ஆரமாகவும் கொண்டு வரையப்படும் வட்டவில் AC-ஐ D புள்ளியில் வெட்டுகிறது.
A -ஐ மையமாகவும் AD -ஐ ஆரமாகவும் கொண்டு வரையப்படும் வட்டவில் AB-ஐ S புள்ளியில் வெட்டுகிறது.
இப்புள்ளி S, கோட்டுத்துண்டு AB -ஐ பொன் விகிதத்தில் பிரிக்கிறது.
பொன் முக்கோணம்[தொகு]

இருசமபக்க முக்கோணம் ABC -ல் கோணங்கள் B, C இரண்டும் சமம்.
இம்முக்கோணத்தில் கோணம் C -ஐ இருசமக்கூறிடக் கிடைக்கும் புது முக்கோணம் CXB, முக்கோணம் ABC -க்கு வடிவொத்ததாக அமையும் பொன் முக்கோணம்.
கோணம் C = 2α என்க.
இக்கோணம் இருசமக்கூறிடப்படுவதால்:
- ஃ (வடிவொத்த முக்கோணங்களின் பண்பு)
- (முக்கோணம் ABC இருசமபக்க முக்கோணம்)
- (வடிவொத்த முக்கோணங்களின் பண்பு)
ஒரு முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180° என்பதால், முக்கோணம் ABC -ன் மூன்று கோணங்களின் கூடுதல்:
- ,
- ஃ α = 36°
முக்கோணம் ABC -ன் கோணங்கள்: 36°-72°-72°.
விரிகோண இருசமபக்க முக்கோணம் AXC (பொன் நோமோன்) -ன் கோணங்கள்: 36°-36°-108°.
XB -ன் நீளம் 1, மற்றும் BC -ன் நீளம் φ என்க.
இருசமபக்க முக்கோணங்களின் பண்பின்படி:
- ;
- ;
முக்கோணங்கள் ABC, CXB இரண்டும் வடிவொத்தவை என்பதால்:
- .
- ஃ , எனவே இங்கு φ பொன் விகிதம். முக்கோணம் ABC பொன் முக்கோணம்.
இதேபோல் பெரிய முக்கோணம் AXC-ன் பரப்பிற்கும் சிறிய முக்கோணம் CXB -ன் பரப்பிற்கும் உள்ள விகிதம் 1/φ (Φ). இவ்விகிதத்தில் முக்கோணங்களின் வரிசையை மாற்றக் கிடைக்கும் விகிதம் φ - 1.
ஐங்கோணம்[தொகு]
ஒரு ஒழுங்கு ஐங்கோணத்தின் ஒரு பக்கத்திற்கும் ஒரு மூலைவிட்டத்திற்குமுள்ள விகிதம் 1/φ. இதன் ஒன்றையொன்று வெட்டிக்கொள்ளும் மூலைவிட்டங்கள் வெட்டிக்கொள்ளும் விகிதம் பொன் விகிதம் ஆகும்.
ஓடோமின் வரைமுறை[தொகு]
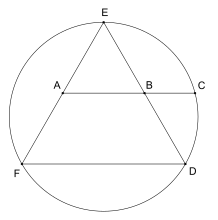
அமெரிக்க கலைஞரும் வடிவவியல் கணித அறிஞருமான ஜார்ஜ் ஓடம் ஒரு சமபக்க முக்கோணத்தைப் பயன்படுத்தி φ -ஐக் காண ஒரு எளிமையான வழியைக் கண்டுபிடித்துள்ளார்:
- ஒரு வட்டத்துக்குள் ஒரு சமபக்கமுக்கோணம் வரைய வேண்டும்.
- அம்முக்கோணத்தின் இரு பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் கோட்டுத்துண்டை நீட்டித்து அதை வட்டத்தை வெட்டச் செய்ய வேண்டும்.
- இரு நடுப்புள்ளிகள் மற்றும் வட்டத்தை வெட்டும் புள்ளி, இம்மூன்றும் பொன் விகிதத்தில் அமையும்.
ஐந்துமுனை நட்சத்திர வடிவம்[தொகு]

ஐந்துமுனையுடைய நட்சத்திரங்களின் வடிவியலில் பொன் விகிதம் முக்கிய பங்கு வகிக்கிறது. விளிம்புகளின் ஒவ்வொரு வெட்டும் பிற விளிம்புகளை பொன் விகிதத்தில் பிரிக்கிறது. மேலும் சிறிய துண்டின் நீளத்திற்கும் இரு வெட்டும் விளிம்புகளுகளால் அடைபடும் துண்டிற்குமுள்ள விகிதம் φ ஆகும். (நட்சத்திர வடிவின் நடுவிலுள்ள ஐங்கோணத்தின் ஒரு பக்கம்).
இந்த நட்சத்திர வடிவில் 10 இருசமபக்க முக்கோணங்கள் (5 குறுங்கோண இருசமபக்க முக்கோணங்கள், 5 விரிகோண இருசமபக்க முக்கோணங்கள்) உள்ளன. இவை எல்லாவற்றிலும் பெரிய பக்கத்திற்கும் சிறிய பக்கத்திற்குமுள்ள விகிதம் φ. 5 குறுங்கோண இருசமபக்க முக்கோணங்களும் பொன் முக்கோணங்கள். 5 விரிகோண இருசமபக்க முக்கோணங்களும் பொன் நோமோன்கள் (golden gnomons).
டாலமியின் தேற்றம்[தொகு]

ஓர் ஒழுங்கு ஐங்கோணத்தின் பொன் விகிதப் பண்புகளை, அதன் ஒரு உச்சியை நீக்கினால் கிடைக்கும் நாற்கரத்தில் டாலமியின் தேற்றத்தைப் பயன்படுத்திக் காணலாம். நாற்கரத்தின் பெரிய விளிம்பும் மூலைவிட்டங்களும் b, மற்றும் சிறிய விளிம்பு a எனில் டாலமியின் தேற்றத்தின்படி:
இச்சமன்பாட்டை -ஆல் வகுத்து, மாற்றி அமைக்க:
இருபடி வாய்ப்பாட்டின்படி நேர்மத் தீர்வு:
- .
மேற்கோள்கள்[தொகு]
- ↑ 1.0 1.1 The golden ratio can be derived by the quadratic formula, by starting with the first number as 1, then solving for 2nd number x, where the ratios (x + 1)/x = x/1 or (multiplying by x) yields: x + 1 = x2, or thus a quadratic equation: x2 − x − 1 = 0. Then, by the quadratic formula, for positive x = (−b + √(b2 − 4ac))/(2a) with a = 1, b = −1, c = −1, the solution for x is: (−(−1) + √((−1)2 − 4·1·(−1)))/(2·1) or (1 + √(5))/2.
- ↑ Weisstein, Eric W., "Golden Ratio Conjugate", MathWorld.
- ↑ Max. Hailperin, Barbara K. Kaiser, and Karl W. Knight (1998). Concrete Abstractions: An Introduction to Computer Science Using Scheme. Brooks/Cole Pub. Co. பன்னாட்டுத் தரப்புத்தக எண்:0-534-95211-9. http://books.google.com/?id=yYyVRueWlZ8C&pg=PA63&dq=continued-fraction+substitute+golden-ratio.
- ↑ Brian Roselle, "Golden Mean Series"
வெளி இணைப்புகள்[தொகு]
- "Golden Section" by Michael Schreiber, Wolfram Demonstrations Project, 2007.
- "The Myth That Will Not Go Away" Mathematical Association of America 2007
- Weisstein, Eric W., "Golden Ratio", MathWorld.
- "Researcher explains mystery of golden ratio". PhysOrg. December 21, 2009..
- Knott, Ron. "The Golden section ratio: Phi". Information and activities by a mathematics professor.
- The Pentagram & The Golden Ratio. Green, Thomas M. Updated June 2005. Archived November 2007. Geometry instruction with problems to solve.





















![{\displaystyle \varphi =[1;1,1,1,\dots ]=1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95682588ffee3530627c3a7b00ff08bbba6e97d4)
![{\displaystyle \varphi ^{-1}=[0;1,1,1,\dots ]=0+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/165d255e32f4b9af1f9144f15302b147fc3fead2)






















