சுரோடிங்கர் சமன்பாடு: திருத்தங்களுக்கு இடையிலான வேறுபாடு
சி தானியங்கி: பகுப்பு:குவாண்டம் இயற்பியல் ஐ மாற்றுகின்றது |
சி பராமரிப்பு using AWB |
||
| வரிசை 1: | வரிசை 1: | ||
{{குவாண்டம் விசையியல்|cTopic=சமன்பாடுகள்}} |
{{குவாண்டம் விசையியல்|cTopic=சமன்பாடுகள்}} |
||
[[இயற்பியல்|இயற்பியலில்]], சிறப்பாக [[குவாண்டம் பொறிமுறை|குவாண்டம் இயங்கியலில்]], '''சுரோடிங்கர் சமன்பாடு''' (''Schrödinger equation'') என்பது இயற்பிய அமைப்பின் ([[அணு|அணுவின்]] உள்ளே உள்ள [[அணுவடித்துகள்|பொருள்கள்]] போன்றவற்றின்) அலைப்பண்பின் இயக்கத்தை விளக்கும் ஓர் அடிப்படைச் சமன்பாடு (ஈடுகோள்). இது மேலும் அடிப்படையான கருதுகோள்களில் இருந்து வருவிக்க முடியாத முதல்கொள்கையான சமன்பாடு. அணுக்கருவைச் சுற்றிவரும் [[எதிர்மின்னி]] போன்ற பொருட்களைப் பொதுவாக தனித் துகள்களாகக் காண்பது வழக்கம் என்றாலும், சில இடங்களில் துல்லியமாக விளக்க வேண்டுமென்றால் அவற்றை அலைகளாகக் கருதவேண்டும். இந்த சுரோடிங்கர் சமன்பாடு என்பது அலைப்பண்புரு (wavefunction) என்னும் ஒரு கற்பனைப் பண்புருவானது எவ்வாறு காலத்தில் மாறுபடுகின்றது என்பதை விரித்துரைக்கும் சமன்பாடு. இந்த அலைப்பண்புரு என்பது '''சை''' (Psi) என்று ஒலிக்கப்படும் [[கிரேக்க மொழி|கிரேக்க]] எழுத்தால் (<math> \psi </math>) குறிக்கப்படும். அலைப்பண்புரு என்பது கற்பனைக் கருத்துரு என்றாலும், அதன் சிக்கலெண் தன்பெருக்குத்தொகை, |
[[இயற்பியல்|இயற்பியலில்]], சிறப்பாக [[குவாண்டம் பொறிமுறை|குவாண்டம் இயங்கியலில்]], '''சுரோடிங்கர் சமன்பாடு''' (''Schrödinger equation'') என்பது இயற்பிய அமைப்பின் ([[அணு|அணுவின்]] உள்ளே உள்ள [[அணுவடித்துகள்|பொருள்கள்]] போன்றவற்றின்) அலைப்பண்பின் இயக்கத்தை விளக்கும் ஓர் அடிப்படைச் சமன்பாடு (ஈடுகோள்). இது மேலும் அடிப்படையான கருதுகோள்களில் இருந்து வருவிக்க முடியாத முதல்கொள்கையான சமன்பாடு. அணுக்கருவைச் சுற்றிவரும் [[எதிர்மின்னி]] போன்ற பொருட்களைப் பொதுவாக தனித் துகள்களாகக் காண்பது வழக்கம் என்றாலும், சில இடங்களில் துல்லியமாக விளக்க வேண்டுமென்றால் அவற்றை அலைகளாகக் கருதவேண்டும். இந்த சுரோடிங்கர் சமன்பாடு என்பது அலைப்பண்புரு (wavefunction) என்னும் ஒரு கற்பனைப் பண்புருவானது எவ்வாறு காலத்தில் மாறுபடுகின்றது என்பதை விரித்துரைக்கும் சமன்பாடு. இந்த அலைப்பண்புரு என்பது '''சை''' (Psi) என்று ஒலிக்கப்படும் [[கிரேக்க மொழி|கிரேக்க]] எழுத்தால் (<math> \psi </math>) குறிக்கப்படும். அலைப்பண்புரு என்பது கற்பனைக் கருத்துரு என்றாலும், அதன் சிக்கலெண் தன்பெருக்குத்தொகை, |
||
<math>|\psi(\mathbf{r},t)|^2 = \psi^* \psi</math> , என்பது அப்பொருளை, அங்கு (அதாவது <math> \mathbf{r} </math> என்னும் அவ்விடத்தில்), t என்னும் அந்நேரத்தில் எதிர்பார்க்கக்ககூடிய ''வாய்ப்பின் மதிப்பளவாகும்''. பொதுவாக இந்த அலைப்பண்புருவானது இடத்தாலும், காலத்தாலும் மாறுபடும் ஒன்று. முன்னைய [[விசைப்பொறியியல்|விசைப்பொறியியலுக்கு]] [[நியூட்டனின் இயக்க விதிகள்|நியூட்டனின் விதிகள்]] எப்படியோ அப்படியே குவாண்டம் பொறிமுறைக்கு ''சுரோடிங்கர் சமன்பாடு'' முக்கியமானதாக விளங்குகிறது. நியூட்டனின் இரண்டாம் விதியைப் போல் இது எளிமையான கணித சமன்பாடு அன்று, மாறாய் இது (பொதுவில்) நேரியல் [[ |
<math>|\psi(\mathbf{r},t)|^2 = \psi^* \psi</math> , என்பது அப்பொருளை, அங்கு (அதாவது <math> \mathbf{r} </math> என்னும் அவ்விடத்தில்), t என்னும் அந்நேரத்தில் எதிர்பார்க்கக்ககூடிய ''வாய்ப்பின் மதிப்பளவாகும்''. பொதுவாக இந்த அலைப்பண்புருவானது இடத்தாலும், காலத்தாலும் மாறுபடும் ஒன்று. முன்னைய [[விசைப்பொறியியல்|விசைப்பொறியியலுக்கு]] [[நியூட்டனின் இயக்க விதிகள்|நியூட்டனின் விதிகள்]] எப்படியோ அப்படியே குவாண்டம் பொறிமுறைக்கு ''சுரோடிங்கர் சமன்பாடு'' முக்கியமானதாக விளங்குகிறது. நியூட்டனின் இரண்டாம் விதியைப் போல் இது எளிமையான கணித சமன்பாடு அன்று, மாறாய் இது (பொதுவில்) நேரியல் [[வகையீட்டுச் சமன்பாடு|பகுதிவகையீட்டுச் சமன்பாடாய்]] இருக்கும். |
||
குவாண்டம் பொறிமுறைக்கான பொதுவான விளக்கத்தில், [[அலைச் சார்பு]] அல்லது [[நிலைக் காவி]] என்று அழைக்கப்படும் குவாண்டம் நிலையே குறிக்கப்பட்ட இயற்பிய தொகுதியை முழுமையாக விளக்குவது. இச்சமன்பாடு [[1926]] ஆம் ஆண்டில் இதனைக் கண்டுபிடித்த [[எர்வின் சுரோடிங்கர்]] என்பவர் பெயரால் வழங்கப்படுகிறது. |
குவாண்டம் பொறிமுறைக்கான பொதுவான விளக்கத்தில், [[அலைச் சார்பு]] அல்லது [[நிலைக் காவி]] என்று அழைக்கப்படும் குவாண்டம் நிலையே குறிக்கப்பட்ட இயற்பிய தொகுதியை முழுமையாக விளக்குவது. இச்சமன்பாடு [[1926]] ஆம் ஆண்டில் இதனைக் கண்டுபிடித்த [[எர்வின் சுரோடிங்கர்]] என்பவர் பெயரால் வழங்கப்படுகிறது. |
||
| வரிசை 7: | வரிசை 7: | ||
[[கோப்பன்னாகன் விளக்கம்|குவாண்டம் இயற்பியலின் நிலைப்பட்ட விளக்கத்தின்படி]] ஒரு இயற்பிய அமைப்பிற்கு உரித்தான உயர்மட்ட வரையறை அதன் அலைப்பண்புருதான். சுரோடிங்கர் சமன்பாடு அணுவடித்துகள்கள், அணுக்கள், மூலக்கூறுகளை மட்டுமன்றி பெரிய அளவிலான அமைப்புகளையும் விவரிப்பதாகும், இப்பேரண்டத்தின் இயக்கத்தையே கூட விவரிக்க இயலும் சாத்தியம் உண்டு. |
[[கோப்பன்னாகன் விளக்கம்|குவாண்டம் இயற்பியலின் நிலைப்பட்ட விளக்கத்தின்படி]] ஒரு இயற்பிய அமைப்பிற்கு உரித்தான உயர்மட்ட வரையறை அதன் அலைப்பண்புருதான். சுரோடிங்கர் சமன்பாடு அணுவடித்துகள்கள், அணுக்கள், மூலக்கூறுகளை மட்டுமன்றி பெரிய அளவிலான அமைப்புகளையும் விவரிப்பதாகும், இப்பேரண்டத்தின் இயக்கத்தையே கூட விவரிக்க இயலும் சாத்தியம் உண்டு. |
||
நியூட்டனின் இரண்டாம் விதியை ஆய்லர்-லெக்ராஞ்சி சமன்பாடு, ஹாமில்டன் சமன்பாடு போன்ற பிற வடிவங்களுக்கு மாற்றி அமைக்க இயல்வதைப் போல, சுரோடிங்கர் சமன்பாட்டினையும் ஹைசன்பர்க்கின் [[ |
நியூட்டனின் இரண்டாம் விதியை ஆய்லர்-லெக்ராஞ்சி சமன்பாடு, ஹாமில்டன் சமன்பாடு போன்ற பிற வடிவங்களுக்கு மாற்றி அமைக்க இயல்வதைப் போல, சுரோடிங்கர் சமன்பாட்டினையும் ஹைசன்பர்க்கின் [[அணி (கணிதம்)|அணி]] இயங்கியல், [[ரிச்சர்டு ஃபெயின்மான்|ரிச்சர்டு ஃபெயின்மானின்]] வழித் தொகைய முறை போன்ற பிற வடிவங்களுக்கு மாற்றி அமைக்க இயலும். மேலும், நியூட்டனின் இரண்டாம் விதியைப் போலவே சுரோடிங்கர் சமன்பாட்டில் குறிக்கப்பெறும் காலம் என்பதன் கருத்துரு சார்பியல் அமைப்புமுறைகளுக்கு ஒத்துவராத வகையிலேயே உள்ளது (சார்பியல் வெளி மற்றும் காலம் ஆகிய இரண்டையுமே ஒரே மதிப்பில்தான் கையாள்கிறது, ஆனால் சுரோடிங்கர் சமன்பாட்டில் காலம் முதல்வரிசை வகையீட்டிலும், வெளி இரண்டாம் வரிசை வகையீட்டிலும் இடம்பெறுவதைக் காண்க, நியூட்டன் விதியிலும் இவ்வாறே உள்ளது.) இச்சிக்கல் ஹைசன்பர்க்கின் அணி இயங்கியலில் இத்துனை தீவிரமாய் இடம்பெறவில்லை, ஃபெயின்மானின் வழித்தொகைய முறையில் முற்றிலுமாகவே இல்லை. |
||
==சமன்பாடு== |
==சமன்பாடு== |
||
| வரிசை 34: | வரிசை 34: | ||
|border |
|border |
||
|border colour = #0073CF |
|border colour = #0073CF |
||
|background colour=#F5FFFA}} |
|background colour=#F5FFFA}} |
||
இங்கு ''m'' என்பது அத்துகளின் நிறை, ''V'' என்பது அதன் நிலையாற்றல், <math>\nabla^2 </math> என்பது லாப்லாசு பணியுரு ஆகும். அடிப்படையில் இச்சமன்பாடு ”மொத்த ஆற்றல் ஆவது இயக்கவாற்றல் மற்றும் நிலையாற்றலின் கூட்டுத்தொகை” என்பதைத்தான் உரைக்கிறது, ஆனால் வகையீட்டுப் பணியுருக்களால் சற்று சிக்கலான வடிவத்தைப் பெற்றிருக்கின்றது. |
இங்கு ''m'' என்பது அத்துகளின் நிறை, ''V'' என்பது அதன் நிலையாற்றல், <math>\nabla^2 </math> என்பது லாப்லாசு பணியுரு ஆகும். அடிப்படையில் இச்சமன்பாடு ”மொத்த ஆற்றல் ஆவது இயக்கவாற்றல் மற்றும் நிலையாற்றலின் கூட்டுத்தொகை” என்பதைத்தான் உரைக்கிறது, ஆனால் வகையீட்டுப் பணியுருக்களால் சற்று சிக்கலான வடிவத்தைப் பெற்றிருக்கின்றது. |
||
| வரிசை 61: | வரிசை 61: | ||
::ஹாமில்டோனிய பணியுரு, <math>\Psi</math> என்ற ஒரு குறிப்பிட்ட அலைப்பண்புருவின் மீது பணியாற்றுகையில் அதன் விளைவு <math>\Psi</math> என்ற அந்த அலைப்பண்புருவின் விகிதசமமாகவே இருக்குமானால், அந்த அலைப்பண்புரு <math>\Psi</math> ஒரு மாறில் நிலையாகும், மேலும் அதன் விகிதத் தொடர்பு மாறிலியான <math>E</math> என்பதே அந்த நிலையின் ஆற்றல் ஆகும். |
::ஹாமில்டோனிய பணியுரு, <math>\Psi</math> என்ற ஒரு குறிப்பிட்ட அலைப்பண்புருவின் மீது பணியாற்றுகையில் அதன் விளைவு <math>\Psi</math> என்ற அந்த அலைப்பண்புருவின் விகிதசமமாகவே இருக்குமானால், அந்த அலைப்பண்புரு <math>\Psi</math> ஒரு மாறில் நிலையாகும், மேலும் அதன் விகிதத் தொடர்பு மாறிலியான <math>E</math> என்பதே அந்த நிலையின் ஆற்றல் ஆகும். |
||
நேரியல் இயற்கணிதத்தின்படி, இச்சமன்பாடு ஒரு [[ |
நேரியல் இயற்கணிதத்தின்படி, இச்சமன்பாடு ஒரு [[ஐகென் மதிப்பு|ஐகன்மதிப்புச்]] சமன்பாடு ஆகும். |
||
முன்பு போலவே, இச்சமன்பாட்டின் மிகப் பிரபலமான வடிவமான (காந்தப்புலம் அற்ற) ஒரு மின்புலத்தில் நகரும் ஒரு தனித்த துகளுக்கான சார்பியற்சாரா சுரோடிங்கர் வடிவம் கீழ்க்காணுமாறு: |
முன்பு போலவே, இச்சமன்பாட்டின் மிகப் பிரபலமான வடிவமான (காந்தப்புலம் அற்ற) ஒரு மின்புலத்தில் நகரும் ஒரு தனித்த துகளுக்கான சார்பியற்சாரா சுரோடிங்கர் வடிவம் கீழ்க்காணுமாறு: |
||
| வரிசை 87: | வரிசை 87: | ||
===அளத்தலும் அறுதியின்மையும்=== |
===அளத்தலும் அறுதியின்மையும்=== |
||
மரபார்ந்த இயற்பியலில் ஒரு பொருள் (அல்லது துகள்), எல்லாத் தருணத்திலும், ஒரு துல்லியமான இடமும் ஒரு துல்லியமான உந்தமும் கொண்டிருக்கும். அப்பொருள் நியூட்டனின் இயக்க விதிகளுக்கு உட்பட்டு நகர்கையில் அதன் இடம் மற்றும் உந்த மதிப்புகளும் நிர்ணயிக்கப்பட்ட முறையில் மாறும். குவாண்டம் இயற்பியலில் பொருட்களுக்கு துல்லியமாக கணக்கிடப்பட்ட பண்பு மதிப்புகள் இருப்பதில்லை, அப்பண்புகள் அளந்தறியப்படும் வேளையில் அவற்றிற்கான மதிப்பு ஒரு நிகழ்தகவு விரவலில் இருந்து [[ |
மரபார்ந்த இயற்பியலில் ஒரு பொருள் (அல்லது துகள்), எல்லாத் தருணத்திலும், ஒரு துல்லியமான இடமும் ஒரு துல்லியமான உந்தமும் கொண்டிருக்கும். அப்பொருள் நியூட்டனின் இயக்க விதிகளுக்கு உட்பட்டு நகர்கையில் அதன் இடம் மற்றும் உந்த மதிப்புகளும் நிர்ணயிக்கப்பட்ட முறையில் மாறும். குவாண்டம் இயற்பியலில் பொருட்களுக்கு துல்லியமாக கணக்கிடப்பட்ட பண்பு மதிப்புகள் இருப்பதில்லை, அப்பண்புகள் அளந்தறியப்படும் வேளையில் அவற்றிற்கான மதிப்பு ஒரு நிகழ்தகவு விரவலில் இருந்து [[சமவாய்ப்பு மாறி|ஏதாவதொரு]] மதிப்பாக பெறப்படுகிறது. சுரோடிங்கர் சமன்பாடு, குறிப்பிட்ட அமைப்பின் குறிப்பிட்ட பண்புகளுக்கான அந்த நிகழ்தகவு விரவல் எது என்பதைக் கணித்துத் தருகிறது, ஆனால் அடிப்படையில் அதனால் ஒரு பண்பினது ஒவ்வொரு அளத்தலுக்குமான துல்லியமான மதிப்பைக் கணிக்க இயலாது. |
||
குவாண்டம் இயங்கியலில் இயல்பாகவே அமைந்துள்ள இந்த அளவைகளின் துல்லியமற்றத்தன்மையின் கூற்றுதான் ஹெய்சன்பர்க்கின் [[அறுதியின்மைக் கொள்கை]] என்பதாகும். இதன்படி ஒரு துகளின் இருப்பிடம் எந்தளவிற்குத் துல்லியமாக அறியப்படுகிறதோ அந்தளவிற்கு அதன் உந்தத்தை அளப்பதில் துல்லியமற்ற தன்மை இருக்கும், அவ்வாறே மாற்றி உரைத்தும் கொள்க. |
குவாண்டம் இயங்கியலில் இயல்பாகவே அமைந்துள்ள இந்த அளவைகளின் துல்லியமற்றத்தன்மையின் கூற்றுதான் ஹெய்சன்பர்க்கின் [[அறுதியின்மைக் கொள்கை]] என்பதாகும். இதன்படி ஒரு துகளின் இருப்பிடம் எந்தளவிற்குத் துல்லியமாக அறியப்படுகிறதோ அந்தளவிற்கு அதன் உந்தத்தை அளப்பதில் துல்லியமற்ற தன்மை இருக்கும், அவ்வாறே மாற்றி உரைத்தும் கொள்க. |
||
18:27, 30 மே 2019 இல் நிலவும் திருத்தம்
| இக்கட்டுரை பின்வரும் கட்டுரைத் தொகுப்பின் கீழ் அடங்கும் |
| குவாண்டம் இயங்கியல் |
|---|
இயற்பியலில், சிறப்பாக குவாண்டம் இயங்கியலில், சுரோடிங்கர் சமன்பாடு (Schrödinger equation) என்பது இயற்பிய அமைப்பின் (அணுவின் உள்ளே உள்ள பொருள்கள் போன்றவற்றின்) அலைப்பண்பின் இயக்கத்தை விளக்கும் ஓர் அடிப்படைச் சமன்பாடு (ஈடுகோள்). இது மேலும் அடிப்படையான கருதுகோள்களில் இருந்து வருவிக்க முடியாத முதல்கொள்கையான சமன்பாடு. அணுக்கருவைச் சுற்றிவரும் எதிர்மின்னி போன்ற பொருட்களைப் பொதுவாக தனித் துகள்களாகக் காண்பது வழக்கம் என்றாலும், சில இடங்களில் துல்லியமாக விளக்க வேண்டுமென்றால் அவற்றை அலைகளாகக் கருதவேண்டும். இந்த சுரோடிங்கர் சமன்பாடு என்பது அலைப்பண்புரு (wavefunction) என்னும் ஒரு கற்பனைப் பண்புருவானது எவ்வாறு காலத்தில் மாறுபடுகின்றது என்பதை விரித்துரைக்கும் சமன்பாடு. இந்த அலைப்பண்புரு என்பது சை (Psi) என்று ஒலிக்கப்படும் கிரேக்க எழுத்தால் () குறிக்கப்படும். அலைப்பண்புரு என்பது கற்பனைக் கருத்துரு என்றாலும், அதன் சிக்கலெண் தன்பெருக்குத்தொகை, , என்பது அப்பொருளை, அங்கு (அதாவது என்னும் அவ்விடத்தில்), t என்னும் அந்நேரத்தில் எதிர்பார்க்கக்ககூடிய வாய்ப்பின் மதிப்பளவாகும். பொதுவாக இந்த அலைப்பண்புருவானது இடத்தாலும், காலத்தாலும் மாறுபடும் ஒன்று. முன்னைய விசைப்பொறியியலுக்கு நியூட்டனின் விதிகள் எப்படியோ அப்படியே குவாண்டம் பொறிமுறைக்கு சுரோடிங்கர் சமன்பாடு முக்கியமானதாக விளங்குகிறது. நியூட்டனின் இரண்டாம் விதியைப் போல் இது எளிமையான கணித சமன்பாடு அன்று, மாறாய் இது (பொதுவில்) நேரியல் பகுதிவகையீட்டுச் சமன்பாடாய் இருக்கும்.
குவாண்டம் பொறிமுறைக்கான பொதுவான விளக்கத்தில், அலைச் சார்பு அல்லது நிலைக் காவி என்று அழைக்கப்படும் குவாண்டம் நிலையே குறிக்கப்பட்ட இயற்பிய தொகுதியை முழுமையாக விளக்குவது. இச்சமன்பாடு 1926 ஆம் ஆண்டில் இதனைக் கண்டுபிடித்த எர்வின் சுரோடிங்கர் என்பவர் பெயரால் வழங்கப்படுகிறது.
குவாண்டம் இயற்பியலின் நிலைப்பட்ட விளக்கத்தின்படி ஒரு இயற்பிய அமைப்பிற்கு உரித்தான உயர்மட்ட வரையறை அதன் அலைப்பண்புருதான். சுரோடிங்கர் சமன்பாடு அணுவடித்துகள்கள், அணுக்கள், மூலக்கூறுகளை மட்டுமன்றி பெரிய அளவிலான அமைப்புகளையும் விவரிப்பதாகும், இப்பேரண்டத்தின் இயக்கத்தையே கூட விவரிக்க இயலும் சாத்தியம் உண்டு.
நியூட்டனின் இரண்டாம் விதியை ஆய்லர்-லெக்ராஞ்சி சமன்பாடு, ஹாமில்டன் சமன்பாடு போன்ற பிற வடிவங்களுக்கு மாற்றி அமைக்க இயல்வதைப் போல, சுரோடிங்கர் சமன்பாட்டினையும் ஹைசன்பர்க்கின் அணி இயங்கியல், ரிச்சர்டு ஃபெயின்மானின் வழித் தொகைய முறை போன்ற பிற வடிவங்களுக்கு மாற்றி அமைக்க இயலும். மேலும், நியூட்டனின் இரண்டாம் விதியைப் போலவே சுரோடிங்கர் சமன்பாட்டில் குறிக்கப்பெறும் காலம் என்பதன் கருத்துரு சார்பியல் அமைப்புமுறைகளுக்கு ஒத்துவராத வகையிலேயே உள்ளது (சார்பியல் வெளி மற்றும் காலம் ஆகிய இரண்டையுமே ஒரே மதிப்பில்தான் கையாள்கிறது, ஆனால் சுரோடிங்கர் சமன்பாட்டில் காலம் முதல்வரிசை வகையீட்டிலும், வெளி இரண்டாம் வரிசை வகையீட்டிலும் இடம்பெறுவதைக் காண்க, நியூட்டன் விதியிலும் இவ்வாறே உள்ளது.) இச்சிக்கல் ஹைசன்பர்க்கின் அணி இயங்கியலில் இத்துனை தீவிரமாய் இடம்பெறவில்லை, ஃபெயின்மானின் வழித்தொகைய முறையில் முற்றிலுமாகவே இல்லை.
சமன்பாடு
காலம்சார் சமன்பாடு
சுரோடிங்கர் சமன்பாட்டின் விரிவான வடிவம் குறிப்பிட்ட இயற்பிய அமைப்புகளைப் பொறுத்து மாறுபடும். அனைத்திலும் மிக பொதுவான வடிவமாவது, காலத்தைப் பொறுத்து மாறுபடும் ஒரு அமைப்பை விவரிக்கும், காலம்சார் சுரோடிங்கர் சமன்பாடே ஆகும்:
காலம்சார் சுரோடிங்கர் சமன்பாடு (பொதுவான வடிவம்)
இங்கு, i என்பது கற்பனை எண், "∂/∂t" என்ற குறியீடு காலத்தைச் சார்ந்த பகுதி வகையீட்டைக் குறிப்பது, ħ என்பது குறுக்கிய பிளாங்க் மாறிலி, Ψ என்பது அந்தக் குவாண்டம் அமைப்பின் அலைப்பண்புரு, மற்றும் என்பது ஹாமில்டனிய பணியுரு ஆகும் (இது ஒரு அமைப்பின் மொத்த ஆற்றலைக் குறிப்பதாகும், அமைப்பைப் பொறுத்து பல்வேறு வடிவங்கள் பெறும்)

சுரோடிங்கர் சமன்பாட்டு வடிவங்களில் மிகப் பிரபலமானதாகிய ஒரு மின்புலத்தில் (காந்தப்புலம் இன்றி) நகரும் ஒரேயொரு தனித் துகளுக்கான சமன்பாடு கீழ்க்காணுமாறு:
காலம்சார் சுரோடிங்கர் சமன்பாடு (தனித்த சார்பியற்சாராத் துகளுக்கு)
இங்கு m என்பது அத்துகளின் நிறை, V என்பது அதன் நிலையாற்றல், என்பது லாப்லாசு பணியுரு ஆகும். அடிப்படையில் இச்சமன்பாடு ”மொத்த ஆற்றல் ஆவது இயக்கவாற்றல் மற்றும் நிலையாற்றலின் கூட்டுத்தொகை” என்பதைத்தான் உரைக்கிறது, ஆனால் வகையீட்டுப் பணியுருக்களால் சற்று சிக்கலான வடிவத்தைப் பெற்றிருக்கின்றது.
மேலே உள்ள வகையீட்டுப் பணியுருக்களை வைத்து பார்க்கையில் இது ஒரு நேரியல் பகுதிவகையீட்டுச் சமன்பாடே ஆகும். இதனை ஒரு விரவல் சமன்பாடு எனவும் கொள்ளலாம், ஆனால் வெப்ப விரவல் சமன்பாட்டினைப் போலன்றி இஃதோர் அலைப்பண்பிற்கான சமன்பாடும் ஆகும், குறிப்பாய் இதன் மாறியில் (Ψ) இடம்பெறும் கற்பனை எண்ணினால் (i) இவ்வாறு கொள்ளப்படும்.
”சுரோடிங்கர் சமன்பாடு” என்பது பொதுவான சமன்பாடு (மேலே முதல் பெட்டி) அல்லது குறிப்பிட்ட சார்பியற்சாரா வடிவம் (மேலே இரண்டாம் பெட்டி) ஆகிய இரண்டையுமே குறிக்கும். பொதுவான வடிவம் மிக அடிப்படையானது, டிராக் சமன்பாடு முதல் குவாண்டம் புலக் கோட்பாடு வரை அனைத்திலும் பயன்படுவது (குறிப்பிட்ட அமைப்பிற்கு ஏற்றவாறான ஒரு சிக்கலான ஹாமில்டோனிய பணியுருவை பதிலிடுவதன் மூலம் இது கைக்கொள்ளப்படும்). சார்பியற்சாரா வடிவமானது மெய்ந்நிலையின் ஒரு எளிமையான தோராய வரையறை ஆகும், இது மிகப் பல சூழல்களில் குறிப்பிடத்தக்க அளவு துல்லியமாக இருந்தாலும் ஒரு சில குறிப்பிட்ட இடங்களில் போதுமான அளவு துல்லியமற்றதாகாவே இருக்கின்றது (சார்பியற்சார் குவாண்டம் பொறிமுறை மற்றும் சார்பியற்சார் குவாண்டம் புலக்கோட்பாடு ஆகிய இடங்கள்).
ஒரு குறிப்பிட்ட அமைப்பிற்கு சுரோடிங்கர் சமன்பாட்டினைப் பயன்படுத்த முதலில் அவ்வமைப்பின் அனைத்து கூறுகளின் (துகள்களின்) இயக்க மற்றும் நிலையாற்றலை உள்ளடக்கிய ஹாமில்டோனிய பணியுரு () ஆக்கப்பட்டு பின்னர் அது சுரோடிங்கர் சமன்பாட்டில் பதிலிடப்படும். இதன் மூலம் கிடைக்கும் சமன்பாடு ஒரு பகுதி வகையீட்டுச் சமன்பாடாய் இருக்கும், இது அதன் மாறியான அலைப்பண்புரு கிடைக்க கணக்கிடப்படும், அவ்வாறு கிடைக்கும் அலைப்பண்புருவில் அவ்வமைப்பின் அனைத்து தகவல்களும் அடங்கும்.
காலம்சாரா சமன்பாடு

அலைப்பண்புருக்கள் நிலையலைகளை உருவாக்க இயலும் என்று காலம்சார் சுரோடிங்கர் சமன்பாடு கணிக்கின்றது, இவை மாறில் நிலை என அறியப்படும் (”அலைமண்டலங்கள்” அல்லது “சுழற்தடங்கள்” எனவும் அழைக்கப்படும், அணு சுழற்தடங்கள் அல்லது மூலக்கூறு சுழற்தடங்கள் போன்று). இந்த மாறில் நிலைகள் தங்களுக்கே உரிய வகையில் முக்கியத்துவம் வாய்ந்தவை, மேலும், இவற்றை வகைப்படுத்திப் புரிந்துகொள்வதன் மூலம் எந்தவொரு நிலையின் காலம்சார் சுரோடிங்கர் சமன்பாட்டினையும் எளிதாய் தீர்த்துவிட இயலும். காலம்சாரா சுரோடிங்கர் சமன்பாடு என்பது இந்த மாறில் நிலைகளை விவரிக்கும் சமன்பாடு ஆகும். (ஹாமில்டோனிய பணியுரு காலச்சார்பு அற்றதாய் இருக்கும் நிலையில் மட்டுமே இது பயன்படும்.)
காலம்சாரா சுரோடிங்கர் சமன்பாடு (பொதுவான வடிவம்)
இச்சமன்பாட்டைச் சொற்களில் உரைப்பதானால் இவ்வாறு உரைக்கலாம்:
- ஹாமில்டோனிய பணியுரு, என்ற ஒரு குறிப்பிட்ட அலைப்பண்புருவின் மீது பணியாற்றுகையில் அதன் விளைவு என்ற அந்த அலைப்பண்புருவின் விகிதசமமாகவே இருக்குமானால், அந்த அலைப்பண்புரு ஒரு மாறில் நிலையாகும், மேலும் அதன் விகிதத் தொடர்பு மாறிலியான என்பதே அந்த நிலையின் ஆற்றல் ஆகும்.
நேரியல் இயற்கணிதத்தின்படி, இச்சமன்பாடு ஒரு ஐகன்மதிப்புச் சமன்பாடு ஆகும்.
முன்பு போலவே, இச்சமன்பாட்டின் மிகப் பிரபலமான வடிவமான (காந்தப்புலம் அற்ற) ஒரு மின்புலத்தில் நகரும் ஒரு தனித்த துகளுக்கான சார்பியற்சாரா சுரோடிங்கர் வடிவம் கீழ்க்காணுமாறு:
காலம்சாரா சுரோடிங்கர் சமன்பாடு (தனித்த சார்பியற்சாராத் துகளுக்கு)
இதன் குறிகளின் விளக்கம் மேலே (காலம்சார் சமன்பாட்டிற்கு) உரைத்தவாறே கொள்க.
இறைச்சி (உட்குறிப்புகள்)
சுரோடிங்கர் சமன்பாடும் அதன் தீர்வுகளும் இயற்பியலைப் பற்றிய சிந்தனைமுறையில் ஒரு மடைமாற்றத்தை ஏற்படுத்தின. சுடோடிங்கர் சமன்பாடு அதன் வகையில் முதலாவது ஆகும், அதன் தீர்வுகள் அக்காலகட்டத்திற்கு மிகுந்த மாறுபட்ட எதிர்பார்க்கப்படாத விளைவுகளுக்கு வழிவகுத்தது.
மொத்த, இயக்க மற்றும் நிலை ஆற்றல்
சுரோடிங்கர் சமன்பாட்டின் அடிப்படையான வடிவம் வழக்கத்திற்கு மாறானதோ எதிர்ப்பாராததோ அல்ல, காரணம் அது ஆற்றல் அழிவின்மை கொள்கையைக் கையாள்வதே. சார்பியற்சாரா சுரோடிங்கர் சமன்பாட்டின் குறியீடுகளை அமைப்பின் மொத்த ஆற்றலைக் குறிப்பது, அமைப்பின் இயக்க ஆற்றல் மற்றும் நிலையாற்றல் ஆகியவற்றின் கூட்டுத்தொகையைக் குறிப்பது என்று விளக்கலாம். இவ்வகையில் இது மரபார்ந்த இயற்பியலில் இருப்பதை போன்றதேதான்.
சொட்டாக்கம்
ஒரு அமைப்பின் குறிப்பிட்ட சில பண்புகளை அளந்துபார்த்தால் அவை சொட்டாக்கம் செய்யப்பட்டிருக்கும் என்று சுரோடிங்கர் சமன்பாடு கணிக்கிறது. சொட்டாக்கம் என்பது அனுமதிக்கப்பட்ட பிரிநிலை மதிப்புகள் மட்டுமே ஒரு பண்பிற்கு அமைவது. எடுத்துக்காட்டாய் ஆற்றல் சொட்டாக்கத்தினைச் சுட்டலாம்: ஒரு அணுவில் இருக்கும் ஒரு எதிர்மின்னியின் ஆற்றல் குறிப்பிட்ட சொட்டாக்கிய ஆற்றல் நிலைகளில் ஒன்றாகவே இருக்கும், இது நிறமாலையியல் மூலம் கண்டறியப்பட்ட ஓர் உண்மையாகும். கோணவுந்தத்தின் சொட்டாக்கம் மற்றுமோர் எடுத்துக்காட்டு. போரின் அணுமாதிரி கோணவுந்தச் சொட்டாக்கத்தை ஒரு கருதுகோளாக கொண்டது, ஆனால் சுரோடிங்கர் சமன்பாட்டிலோ இஃதோர் கணிப்பாகவே பெறப்படுகிறது.
அளத்தலும் அறுதியின்மையும்
மரபார்ந்த இயற்பியலில் ஒரு பொருள் (அல்லது துகள்), எல்லாத் தருணத்திலும், ஒரு துல்லியமான இடமும் ஒரு துல்லியமான உந்தமும் கொண்டிருக்கும். அப்பொருள் நியூட்டனின் இயக்க விதிகளுக்கு உட்பட்டு நகர்கையில் அதன் இடம் மற்றும் உந்த மதிப்புகளும் நிர்ணயிக்கப்பட்ட முறையில் மாறும். குவாண்டம் இயற்பியலில் பொருட்களுக்கு துல்லியமாக கணக்கிடப்பட்ட பண்பு மதிப்புகள் இருப்பதில்லை, அப்பண்புகள் அளந்தறியப்படும் வேளையில் அவற்றிற்கான மதிப்பு ஒரு நிகழ்தகவு விரவலில் இருந்து ஏதாவதொரு மதிப்பாக பெறப்படுகிறது. சுரோடிங்கர் சமன்பாடு, குறிப்பிட்ட அமைப்பின் குறிப்பிட்ட பண்புகளுக்கான அந்த நிகழ்தகவு விரவல் எது என்பதைக் கணித்துத் தருகிறது, ஆனால் அடிப்படையில் அதனால் ஒரு பண்பினது ஒவ்வொரு அளத்தலுக்குமான துல்லியமான மதிப்பைக் கணிக்க இயலாது.
குவாண்டம் இயங்கியலில் இயல்பாகவே அமைந்துள்ள இந்த அளவைகளின் துல்லியமற்றத்தன்மையின் கூற்றுதான் ஹெய்சன்பர்க்கின் அறுதியின்மைக் கொள்கை என்பதாகும். இதன்படி ஒரு துகளின் இருப்பிடம் எந்தளவிற்குத் துல்லியமாக அறியப்படுகிறதோ அந்தளவிற்கு அதன் உந்தத்தை அளப்பதில் துல்லியமற்ற தன்மை இருக்கும், அவ்வாறே மாற்றி உரைத்தும் கொள்க.
சுரோடிங்கர் சமன்பாடு ஒரு துகளின் (அல்லது அமைப்பின்) அலைப்பண்புருவின் (நிர்ணயிக்கப்பட்ட) காலம்சார் மாற்றத்தை விவரிக்கின்றது. எத்தனைதான் அலைப்பண்புரு துல்லியமாக அறியப்பட்டாலும், ஒரு குறிப்பிட்ட பண்பை அறிய அதன் மீது நிகழ்த்தப்படும் அளவையின் விடை துல்லியமற்றதாகவே இருக்கும்.
குவாண்டம் புரையூடல்
மரபார்ந்த இயற்பியலில், ஒரு பொருள் ஒரு தடையை எதிர்கொள்கையில் அத்தடையைத் தாண்ட போதுமான ஆற்றல் அப்பொருளுக்கு இல்லை என்றால் அதனால் அத்தடையைத் தாண்ட இயலாது. எடுத்துக்காட்டாய், ஒரு பெரிய மலையின் அடியிலிருந்து உச்சிநோக்கி ஒரு பந்து உருட்டப்படுகையில், அது சிறிது உயரம்வரை சென்றுவிட்டுப் பின் மீண்டும் கீழ்நோக்கி உருளத் தொடங்கும், காரணம் அதற்கு அம்மலையைக் கடந்து அடுத்த பக்கத்திற்கு வரத் தேவையான ஆற்றல் இல்லை. ஆனால், சுரோடிங்கர் சமன்பாட்டின்படி அப்பந்து மலையின் மறுபுறத்தை அடைவதற்கான நிகழ்தகவு சிறிதளவு உண்டு. இதுவே குவாண்டம் புரையூடல் எனப்படுகிறது. இது அறுதின்மையோடு தொடர்புடையது: பந்து மலையின் ஒருபுறம் இருப்பதாக தோன்றினாலும், அதன் இருப்பிடத்தின் அறுதியின்மை காரணமாக அப்பந்தினை மலையின் மற்றொருபுறத்தில் காண்பதற்கான சாத்தியமும் சிறிது ஏற்படுகிறது (பந்து போன்ற பெரிய அளவிலான பொருள்களில் இவ்விளைவினைக் கண்டறிவது மிக அரிது, ஆனால், எதிர்மின்னி போன்ற மிகச் சிறிய துகள்களில் இவ்விளைவை எளிதாய் காணலாம்.)
துகள்களை அலைகளாக கருதுதல்

சார்பியற்சாரா சுரோடிங்கர் சமன்பாடானது அலைச் சமன்பாடு என்று அறியப்படும் ஒரு வகை பகுதி வகையீட்டுச் சமன்பாடு ஆகும். இதனால் அலைகளுக்கு உரிய இயல்புகளைத் துகள்களும் வெளிப்படுத்தும் என்று சொல்லப்படுகிறது. மிக அண்மைக்கால விளக்கங்களில் இந்த விவரம் நேரெதிராக சொல்லப்படுகிறது - குவாண்டம் நிலை, அதாவது அலைத்தன்மை, ஒன்றே உண்மையான இயற்பிய மெய்ந்நிலை, பொருத்தமான சூழல்களில் அது துகள் போன்ற இயல்புகளையும் வெளிப்படுத்தக் கூடியது.
அலைகள் அடிக்கடி காட்டும் இயல்புகளுக்கான ஒரு பிரபலமான எடுத்துக்காட்டு இரட்டைப் பிளவு விளிம்பு வளைவு ஆகும், இயல்பில் இவ்விளைவோடு துகள்களை இணைத்துப் பார்க்க இயலாது. இரண்டு பிளவுகளின் வாயிலாக வெளிவரும் அலை பிரிவுகள் ஒன்றாய்ப் படர்கையில் சில இடங்களில் ஒன்றை ஒன்று நீக்கியும் சில இடங்களில் ஒன்றோடு ஒன்று சேர்ந்தும் ஒரு சிக்கலான படிவத்தினை உருவாக்கும். பொதுவாய், ஒரு துகளை இரட்டைப் பிளவுகளை நோக்கி எறிவதன் மூலம் இவ்வாறான சிக்கலான படிவத்தை யாரும் எதிர்ப்பார்க்க இயலாது, காரணம் அந்தத் துகள் இரண்டு பிளவுகளில் ஏதேனும் ஒன்றன் வழியாகத்தான் செல்ல இயலும், இரண்டுன் ஊடாகவும் அதனால் செல்ல இயலாது.
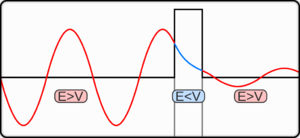
ஆனால், சுரோடிங்கர் சமன்பாடு ஒரு அலைச் சமன்பாடு என்பதனால் அதன்படி இரட்டைப் பிளவை நோக்கி எறியப்படும் ஒரு தனித் துகள் அலைகள் உருவாக்குவது போன்ற ஒரு சிக்கலான படிவத்தையே தானும் உருவாக்கும் (இடப்புறம் உள்ள படம்). இந்தச் சிக்கலான படிவத்தினைப் பெற சோதனையைப் பலமுறை நிகழ்த்த வேண்டும். இந்தப் படிவம் தோன்றுதல் ஒவ்வொரு எதிர்மின்னியும் ஒரே நேரத்தில் இரண்டு பிளவுகள் வழியாகவும் செல்கின்றன என்பதற்கான சான்று ஆகும். இது உள்ளுணர்விற்கு எதிராய் தோன்றினாலும் இதுவே சரியான கணிப்பு ஆகும், குறிப்பாய் எதிர்மின்னி மற்றும் நொதுமியின் விளிம்புவளைவுகள் நன்கு புரிந்துகொள்ளப்பட்டு பல அறிவியல் துறைகளிலும் பரவலாக பயன்கொள்ளப்படுகின்றன.
விளிம்பு வளைவைப் போலவே துகள்கள் மேற்பொருந்தல் மற்றும் குறுக்கீட்டுவிளைவு ஆகியவற்றையும் வெளிப்படுத்துகின்றன.
மேற்பொருந்தல் பண்பு ஒரு துகள் ஒரே நேரத்தில் இரண்டு அல்லது மேற்பட்ட நிலைகளில் வெவ்வேறு மரபார்ந்த (அறுதியான) பண்பு மதிப்புகளோடு ஒரு குவாண்டம் மேற்பொருந்தல் நிலையில் இருக்க அனுமதிக்கிறது. எடுத்துக்காட்டய், ஒரு துகள் ஒரே நேரத்தில் பல ஆற்றல் மதிப்புகளைக்கொண்டு இருக்கலாம், அதே போல் பல்வேறு இடங்களிலும் அத்துகள் ஒரே நேரத்தில் இருக்கலாம். மேலே உள்ள எதிர்மின்னி விளிம்புவளைவு எடுத்துக்காட்டில், ஒரு துகள் ஒரே நேரத்தில் இரண்டு பிளவுகளின் வழியாகவும் செல்லக் கூடியதாய் இருக்கிறது. பல நிலைகள் மேற்பொருந்தி இருந்தாலும் அந்த மேற்பொருந்தி இருக்கும் நிலையானது ஒரே ஒரு குவாண்டம் நிலையே ஆகும், இது மரபார்ந்த உள்ளுணர்வுக்கு ஒத்துப்போகத ஒன்றாய் இருந்தாலும் இது சோதனைகளால் உறுதி செய்யப்படுகிறது.
அலைப்பண்புருவைப் பற்றிய விளக்கம்
சுரோடிங்கர் சமன்பாடு ஒரு அமைப்பிற்கு சாத்தியமான அலைப்பண்புருக்களைக் கணக்கிடவும், அவை காலத்தைப் பொறுத்து எவ்வாறு இயக்கஞ்சார்ந்து மாறுபடுகின்றன என்பதையும் அறியவும் ஒரு வழிமுறையை அளிக்கிறது. ஆனால் அதே சுரோடிங்கர் சமன்பாடு நேரடியாகவும் துல்லியமாகவும் அலைப்பண்புரு என்றால் என்ன என்று உரைக்கவில்லை. குவாண்டம் இயக்கவியலுக்கான விளக்கங்கள் அலைப்பண்பு, அதன் அடிப்படையான உண்மை மற்றும் இவை சார்ந்த ஆய்வுகளின் அளவைகள் ஆகியவற்றிற்கு இடையிலான தொடர்பு என்ன என்பது போன்ற கேள்விகளுக்கு விடைகாண முயல்கின்றன.
இதன் ஒரு முக்கிய பாங்கு சுரோடிங்கர் சமன்பாட்டிற்கும் அலைப்பண்புரு நொறுங்குதலுக்கும் இடையிலான தொடர்பு ஆகும். பழைய கோப்பன்னாகன் விளக்கத்தில், துகள்கள் பொதுவில் சுரோடிங்கர் சமன்பாட்டையே பின்பற்றும், அலைப்பண்புரு நொறுக்கம் நிகழ்வதற்கு முன்புவரை, அலைப்பண்புரு நொறுங்கினால் அவை முற்றிலும் வேறு வகையில் நடந்துகொள்ளும். குவாண்டம் பிணைப்பிழைப்புக் கோட்பாட்டின் வருகை (எவரெட் என்பவரின் பல்-உலகு விளக்கம் மற்றும் இசைவுறு வரலாறுகள் போன்ற) மாற்று அணுகுமுறைகளுக்கு வழிவகுத்தது, இவை எப்பொழுதுமே சுரோடிங்கரின் சமன்பாட்டைப் பொருந்தியே இருக்கும், மேலும் அலைப்பண்புரு நொறுக்கம் சுரோடிங்கர் சமன்பாட்டின் ஒரு தொடர்விளைவாகவே விளக்கப்பட வேண்டும்.
வரலாற்றுப் பின்புலமும் சமன்பாட்டை அமைத்தலும்
துகள்களுக்கான அலைச் சமன்பாடு
அடிக்குறிப்புகள்
- ↑ Physics for Scientists and Engineers – with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman







![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=\left[{\frac {-\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} ,t)\right]\Psi (\mathbf {r} ,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4894f9a205c471cb012351a1fccdd01285b6f11c)