உடுவுரு

உடுவுரு

உடுவுருவின் உள்வட்டப்புள்ளியுரு உருவாக்கம்.

(^x⁄_a)² + (^y⁄_b)² = r², (a + b = 1)-நீள்வட்டக் குடும்பத்தின் சூழ்வாக பெறப்பட்ட உடுவுரு-x^2⁄₃ + y^2⁄₃ = r^2⁄₃ .

செங்குத்துச் சுவரொன்றிலிருந்து நழுவும் ஏணி (வலப்பக்க-மேல் காற்பகுதியிலுள்ள நிறமிட்டக் கோடுகள்), மற்ற காற்பகுதிகளில் அதன் எதிரொளிப்புகள் ஆகியவற்றின் சூழ்வானது ஒரு உடுவுருவாக அமைகிறது. நடுப்புல்ளிகள் வட்டத்தையும் பிற புள்ளிகள் நீள்வட்டத்தையும் உருவாக்குகின்றன. In the SVG file, hover over a ladder to highlight it.

நீள்வட்டத்தின் மலரியாக உடுவுரு.

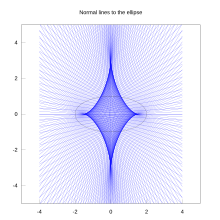
கணிதத்தில், உடுவுரு (astroid) என்பது ஒரு குறிப்பிட்ட வகையான சிறுசில்லியாகும். இது நான்கு கூர்களுடைய ஒரு உள்வட்டப்புள்ளியுரு. குறிப்பாக, ஒரு வட்டமானது அதன் ஆரத்தைப்போல நான்கு மடங்கு ஆரமுள்ள நிலையான வட்டத்துக்குள் வழுக்காமல் உருளும்போது அவ்வுருளும் வட்டத்தின் மீதுள்ள ஒரு புள்ளியின் இயங்குவரையாகும். இரட்டைப் பிறப்பாக்கத்தில், உடுவுருவானது ஒரு வட்டமானது அதன் ஆரத்தைப்போல 4/3 மடங்கு ஆரமுள்ள நிலையான வட்டத்துக்குள் நழுவாமல் உருளும்போது அவ்வுருளும் வட்டத்தின் மீதுள்ள ஒரு புள்ளியின் இயங்குவரையாகும். ஒவ்வொரு முனையும் ஒரு ஆய அச்சின் மீதே இருக்குமாறு நகரும் நிலையான நீளமுள்ளதொரு கோட்டுத்துண்டின் சூழ்வாகவும் உடுவுருவை வரையறுக்கலாம். எனவே ஆர்க்கிமிடீசின் வளைக்கவராயத்தின் நகரும் பட்டைத்துண்டின் சூழ்வும் ஒரு உடுவுருவாகும். உடுவுருவின் தற்கால ஆங்கிலப் பெயரான astroid என்பது "விண்மீனைக்" குறிக்கும் கிரேக்கச் சொல்லில் இருந்து ("Astrois") பெறப்பட்டது.

சமன்பாடுகள்

• நிலையான வட்டத்தின் ஆரம் a எனில், உடுவுருவின் கார்ட்டீசியச் சமன்பாடு:

$x^{2/3}+y^{2/3}=a^{2/3}.\,$

• துணையலகுச் சமன்பாடுகள்

${\begin{aligned}&x=a\cos ^{3}t={a \over 4}(3\cos t+\cos 3t),\\[6pt]&y=a\sin ^{3}t={a \over 4}(3\sin t-\sin 3t).\end{aligned}}$

• கோணதூரச் சமன்பாடு:

$r={\frac {a}{(\cos ^{2/3}\theta +\sin ^{2/3}\theta )^{3/2}}}.$

• மற்றொருமொரு பல்லுறுப்புக்கோவைச் சமன்பாடு:

$(x^{2}+y^{2}-a^{2})^{3}+27a^{2}x^{2}y^{2}=0.\,$

இச்சமன்பாட்டிலிருந்து உடுவுருவானது ஒரு ஆறாம் படியுள்ள மெய் இயற்கணித வளைவரையென அறியலாம்.

பல்லுறுப்புக்கோவைச் சமன்பாட்டின் நிறுவல்

கார்ட்டீசியச் சமன்பாட்டிலிருந்து பல்லுறுப்புக்கோவைச் சமன்பாட்டைப் பெறலாம்:

$x^{2/3}+y^{2/3}=a^{2/3}.\,$

இதனை இருபுறமும் முப்படிக்கு உயர்த்த,

$(x^{2/3}+y^{2/3})^{3}=a^{2}.\,$

$x^{6/3}+3x^{4/3}y^{2/3}+3x^{2/3}y^{4/3}+y^{6/3}=a^{6/3}\,$

$x^{2}+3x^{2/3}y^{2/3}(x^{2/3}+y^{2/3})+y^{2}=a^{2}\,$

$x^{2}+y^{2}-a^{2}=-3x^{2/3}y^{2/3}(x^{2/3}+y^{2/3})\,$

மீண்டும் இருபுறமும் முப்படிக்கு உயர்த்த,

$(x^{2}+y^{2}-a^{2})^{3}=-27x^{2}y^{2}(x^{2/3}+y^{2/3})^{3}\,$

$(x^{2}+y^{2}-a^{2})^{3}=-27x^{2}y^{2}a^{2}\,$

(அல்லது)

$(x^{2}+y^{2}-a^{2})^{3}+27x^{2}y^{2}a^{2}=0.\,$

அளவைகள்

• அடைபெறும் பரப்பளவு:

${\frac {3}{8}}\pi a^{2}$

• வில்லின் நீளம்

$6a$

• x-அச்சை பொறுத்து அடைபெறும் பரப்பின் சுழற்சியால் உருவாகும் திண்மத்தின் கனவளவு

${\frac {32}{105}}\pi a^{3}$

x-அச்சை பொறுத்து அடைபெறும் பரப்பின் சுழற்சியால் உருவாகும் திண்மத்தின் மேற்பரப்பளவு

${\frac {12}{5}}\pi a^{2}$

பண்புகள்

• மெய்யெண் தளத்தில் நான்கு கூர் [[ஓர்மை (கணிதம்)|ஓர்மைப்புள்ளிகள் (விண்மீனின் முனைப்புள்ளிகள்), சிக்கலெண் தளத்தில் முடிவிலியிலமையும் இரு கூர் ஓர்மைப்புள்ளிகள், நான்கு சிக்கலெண் இரட்டைப் புள்ளிகளென உடுவுருக்கு பத்து ஓர்மைப்புள்ளிகள் உள்ளன.
• உடுவுருவின் இரட்டை வளைவரை, ஒரு குறுக்குவடிவ வளைவரையாகும். இக் குறுக்குவடிவ வளைவரையின் சமன்பாடு: $\textstyle x^{2}y^{2}=x^{2}+y^{2}.$
• ஒரு உடுவுருவின் மலரியானது அவ் வுடுவுருவைப் போல இருமடங்கு பெரிய உடுவுருவாக இருக்கும்.
• உடுவுருவுக்கு, ஒவ்வொரு திசைப்போக்கிலும் ஒரேயொரு தொடுகோடு மட்டுமே இருக்கும்.

மேற்கோள்கள்

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. பக். 4–5,34–35,173–174. பன்னாட்டுத் தரப்புத்தக எண்:0-486-60288-5. https://archive.org/details/catalogspecialpl00lawr. 
• Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. பக். 10–11. பன்னாட்டுத் தரப்புத்தக எண்:0-14-011813-6. 
• R.C. Yates (1952). "Astroid". A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards. பக். 1 ff.. 

வெளியிணைப்புகள்

விக்கிமீடியா பொதுவகத்தில்,
Astroid
என்பதில் ஊடகங்கள் உள்ளன.

• Hazewinkel, Michiel, ed. (2001), "Astroid", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104
• Weisstein, Eric W., "Astroid", MathWorld.
• "Astroid" at The MacTutor History of Mathematics archive
• "Astroid" at The Encyclopedia of Remarkable Mathematical Forms
• Article on 2dcurves.com
• Visual Dictionary Of Special Plane Curves, Xah Lee
• Bars of an Astroid by Sándor Kabai, The Wolfram Demonstrations Project.