கட்டற்ற கலைக்களஞ்சியமான விக்கிப்பீடியாவில் இருந்து.
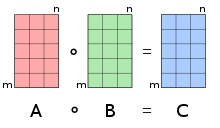
ஆடமார்டு பெருக்கல் செயலானது இரு சமவரிசை அணிகளுக்கு இடையே செயற்பட்டு அதே வரிசையுள்ள புது அணியைத் தருகிறது கணிதத்தில் ஆடமார்டு பெருக்கல் (Hadamard product ) அல்லது உறுப்புவாரிப் பெருக்கல் (entrywise product )[1] அணிகளுக்கிடையான ஈருறுப்புச் செயலியாகும் . இதில் சமவரிசையுள்ள இரு அணிகளைக் கொண்டு மற்றொரு புது அணி உருவாக்கப்படுகிறது. இரு அணிகளில், ஒரு அணியின் உறுப்பு ஒவ்வொன்றையும் அதற்கு ஒத்த இடத்தில் இரண்டாவது அணியில் உள்ள உறுப்புடன் பெருக்கிக் கிடைக்கும் விடையானது புது அணியின் அதே ஒத்த உறுப்பாக எழுதிக் கொள்ளப்படும். அதாவது, ஒரு அணியின் ij உறுப்பானது மற்றதன் ij உறுப்புடன் பெருக்கக்கிடைக்கும் விடையானது புது அணியின் ij உறுப்பாக எழுதப்படுகிறது. பொதுவான அணிப்பெருக்கலில் இருந்து இச்செயல் மாறுபட்ட ஒன்றாகும்.
இச்செயல் சேர்ப்புப் பண்பும் பங்கீட்டுப் பண்பும் உடையது. அணிப்பெருக்கலைப் போலில்லாமல் இப்பெருக்கல் பரிமாற்றுத்தன்மையும் கொண்டது.
A
,
B
{\displaystyle A,B}
m
×
n
{\displaystyle m\times n}
A
∘
B
{\displaystyle A\circ B}
m
×
n
{\displaystyle m\times n}
(
A
∘
B
)
i
,
j
=
(
A
)
i
,
j
(
B
)
i
,
j
{\displaystyle (A\circ B)_{i,j}=(A)_{i,j}(B)_{i,j}}
A
{\displaystyle A}
m
×
n
{\displaystyle m\times n}
B
{\displaystyle B}
p
×
q
{\displaystyle p\times q}
m
≠
p
{\displaystyle m\not =p}
n
≠
q
{\displaystyle n\not =q}
A
,
B
{\displaystyle A,B}
A
∘
B
{\displaystyle A\circ B}
எடுத்துக்காட்டு [ தொகு ] 3×3 வரிசை அணிகள் A , B இன் ஆடமார்டு பெருக்கல்:
A
=
(
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
)
{\displaystyle A=\left({\begin{array}{ccc}\mathrm {a} _{11}&\mathrm {a} _{12}&\mathrm {a} _{13}\\\mathrm {a} _{21}&\mathrm {a} _{22}&\mathrm {a} _{23}\\\mathrm {a} _{31}&\mathrm {a} _{32}&\mathrm {a} _{33}\end{array}}\right)}
B
=
(
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
)
{\displaystyle B=\left({\begin{array}{ccc}\mathrm {a} _{11}&\mathrm {a} _{12}&\mathrm {a} _{13}\\\mathrm {a} _{21}&\mathrm {a} _{22}&\mathrm {a} _{23}\\\mathrm {a} _{31}&\mathrm {a} _{32}&\mathrm {a} _{33}\end{array}}\right)}
A
∘
B
=
(
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
)
∘
(
b
11
b
12
b
13
b
21
b
22
b
23
b
31
b
32
b
33
)
=
(
a
11
b
11
a
12
b
12
a
13
b
13
a
21
b
21
a
22
b
22
a
23
b
23
a
31
b
31
a
32
b
32
a
33
b
33
)
{\displaystyle A\circ B=\left({\begin{array}{ccc}\mathrm {a} _{11}&\mathrm {a} _{12}&\mathrm {a} _{13}\\\mathrm {a} _{21}&\mathrm {a} _{22}&\mathrm {a} _{23}\\\mathrm {a} _{31}&\mathrm {a} _{32}&\mathrm {a} _{33}\end{array}}\right)\circ \left({\begin{array}{ccc}\mathrm {b} _{11}&\mathrm {b} _{12}&\mathrm {b} _{13}\\\mathrm {b} _{21}&\mathrm {b} _{22}&\mathrm {b} _{23}\\\mathrm {b} _{31}&\mathrm {b} _{32}&\mathrm {b} _{33}\end{array}}\right)=\left({\begin{array}{ccc}\mathrm {a} _{11}\,\mathrm {b} _{11}&\mathrm {a} _{12}\,\mathrm {b} _{12}&\mathrm {a} _{13}\,\mathrm {b} _{13}\\\mathrm {a} _{21}\,\mathrm {b} _{21}&\mathrm {a} _{22}\,\mathrm {b} _{22}&\mathrm {a} _{23}\,\mathrm {b} _{23}\\\mathrm {a} _{31}\,\mathrm {b} _{31}&\mathrm {a} _{32}\,\mathrm {b} _{32}&\mathrm {a} _{33}\,\mathrm {b} _{33}\end{array}}\right)}
பண்புகள் [ தொகு ]
A
∘
B
=
B
∘
A
,
A
∘
(
B
∘
C
)
=
(
A
∘
B
)
∘
C
,
A
∘
(
B
+
C
)
=
A
∘
B
+
A
∘
C
.
{\displaystyle {\begin{aligned}A\circ B&=B\circ A,\\A\circ (B\circ C)&=(A\circ B)\circ C,\\A\circ (B+C)&=A\circ B+A\circ C.\end{aligned}}}
ஆடமார்டு பெருக்கலின் கீழ், இரு m x n அணிகளின் முற்றொருமை அணியானது அனைத்து உறுப்புகளும் 1 ஆகவுள்ள m x n அணியாக இருக்கும். இவ்வணியானது, வழமையான அணிப்பெருக்கலின் கீழ் அமையும் முற்றொருமை அணியிலிருந்து வேறுபட்டதாகும்.
அனைத்து உறுப்புகளும் பூச்சியமற்றதாக இருந்தால், இருந்தால் மட்டுமே ஒரு அணிக்கு ஆடமார்டு பெருக்கலின் கீழ் நேர்மாறு இருக்கும்.[2]
x
{\displaystyle x}
y
{\displaystyle y}
x
{\displaystyle x}
முதன்மை மூலைவிட்டமாகக் கொண்ட மூலைவிட்ட அணி
D
x
,
{\displaystyle D_{x},}
y
{\displaystyle y}
முதன்மை மூலைவிட்டமாகக் கொண்ட மூலைவிட்ட அணி
D
y
{\displaystyle D_{y}}
[3]
x
∗
(
A
∘
B
)
y
=
t
r
(
D
x
∗
A
D
y
B
T
)
{\displaystyle x^{*}(A\circ B)y=\mathrm {tr} \left(D_{x}^{*}AD_{y}B^{T}\right)}
x
∗
{\displaystyle x^{*}}
x
{\displaystyle x}
இடமாற்று இணையணி ஆகும்.
∑
i
(
A
∘
B
)
i
,
j
=
(
B
T
A
)
j
,
j
.
{\displaystyle \sum _{i}(A\circ B)_{i,j}=\left(B^{T}A\right)_{j,j}.}
[4]
∑
j
(
A
∘
B
)
i
,
j
=
(
A
B
T
)
i
,
i
.
{\displaystyle \sum _{j}(A\circ B)_{i,j}=\left(AB^{T}\right)_{i,i}.}
rank
(
A
∘
B
)
≤
rank
(
A
)
rank
(
B
)
{\displaystyle \operatorname {rank} (A\circ B)\leq \operatorname {rank} (A)\operatorname {rank} (B)}
மேற்கோள்கள் [ தொகு ]